Latitude - Latitude

Na geografia , a latitude é uma coordenada geográfica que especifica a posição norte - sul de um ponto na superfície da Terra. Latitude é um ângulo (definido abaixo) que varia de 0 ° no Equador a 90 ° (Norte ou Sul) nos pólos. Linhas de latitude constante, ou paralelas , correm de leste a oeste como círculos paralelos ao equador. A latitude é usada junto com a longitude para especificar a localização precisa dos recursos na superfície da Terra. Por si só, o termo latitude deve ser considerado como a latitude geodésica conforme definido abaixo. Resumidamente, a latitude geodésica em um ponto é o ângulo formado pelo vetor perpendicular (ou normal ) à superfície elipsoidal daquele ponto e o plano equatorial. Também são definidas seis latitudes auxiliares que são usadas em aplicações especiais.
Fundo
Dois níveis de abstração são empregados na definição de latitude e longitude. Na primeira etapa, a superfície física é modelada pelo geóide , uma superfície que se aproxima do nível médio do mar sobre os oceanos e sua continuação sob as massas de terra. A segunda etapa é aproximar o geóide por uma superfície de referência matematicamente mais simples. A escolha mais simples para a superfície de referência é uma esfera , mas o geóide é modelado com mais precisão por um elipsóide. As definições de latitude e longitude em tais superfícies de referência são detalhadas nas seções a seguir. Linhas de latitude e longitude constantes juntas constituem uma gratícula na superfície de referência. A latitude de um ponto na superfície real é a do ponto correspondente na superfície de referência, sendo a correspondência ao longo da normal à superfície de referência, que passa pelo ponto na superfície física. Latitude e longitude junto com alguma especificação de altura constituem um sistema de coordenadas geográficas conforme definido na especificação da norma ISO 19111.
Uma vez que existem muitos elipsóides de referência diferentes , a latitude precisa de um recurso na superfície não é única: isso é enfatizado no padrão ISO que afirma que "sem a especificação completa do sistema de referência de coordenadas, coordenadas (isto é, latitude e longitude) são ambíguos na melhor das hipóteses e sem sentido na pior ". Isso é de grande importância em aplicações precisas, como um Sistema de Posicionamento Global (GPS), mas no uso comum, onde a alta precisão não é necessária, o elipsóide de referência geralmente não é indicado.
Em textos em inglês, o ângulo de latitude, definido abaixo, é geralmente denotado pela letra grega minúscula phi ( ϕ ou φ ). É medido em graus , minutos e segundos ou graus decimais , ao norte ou ao sul do equador. Para fins de navegação, as posições são fornecidas em graus e minutos decimais. Por exemplo, o farol The Needles está em 50 ° 39.734′N 001 ° 35.500′W.
Este artigo se refere a sistemas de coordenadas para a Terra: pode ser adaptado para cobrir a Lua, planetas e outros objetos celestes ( latitude planetográfica ).
Para uma breve história, consulte História da latitude .
Determinação
Na navegação celestial , a latitude é determinada com o método da altitude dos meridianos . Uma medição mais precisa da latitude requer uma compreensão do campo gravitacional da Terra, seja para estabelecer teodolitos ou para determinar as órbitas dos satélites GPS. O estudo da figura da Terra juntamente com seu campo gravitacional é a ciência da geodésia .
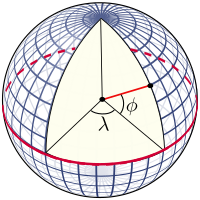
Latitude na esfera
A gratícula na esfera
A gratícula é formada pelas linhas de latitude e longitude constantes, que são construídas com referência ao eixo de rotação da Terra. Os pontos de referência primários são os pólos onde o eixo de rotação da Terra intercepta a superfície de referência. Os planos que contêm o eixo de rotação cruzam a superfície nos meridianos ; e o ângulo entre qualquer plano meridiano e aquele que passa por Greenwich (o Meridiano Principal ) define a longitude: os meridianos são linhas de longitude constante. O plano que passa pelo centro da Terra e perpendicular ao eixo de rotação cruza a superfície em um grande círculo chamado Equador . Planos paralelos ao plano equatorial cruzam a superfície em círculos de latitude constante; esses são os paralelos. O Equador tem uma latitude de 0 °, o Pólo Norte tem uma latitude de 90 ° Norte (escrito 90 ° N ou + 90 °) e o Pólo Sul tem uma latitude de 90 ° Sul (escrito 90 ° S ou −90 ° ) A latitude de um ponto arbitrário é o ângulo entre o plano equatorial e a normal à superfície naquele ponto: a normal à superfície da esfera está ao longo do vetor do raio.
A latitude, conforme definida desta forma para a esfera, é freqüentemente denominada latitude esférica, para evitar ambigüidade com a latitude geodésica e as latitudes auxiliares definidas nas seções subsequentes deste artigo.
Latitudes nomeadas na Terra
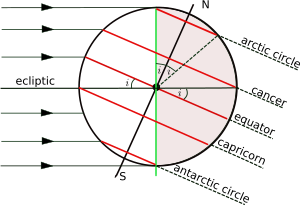
Além do equador, quatro outros paralelos são importantes:
circulo Ártico 66 ° 34 ′ (66,57 °) N Trópico de Câncer 23 ° 26 ′ (23,43 °) N Trópico de Capricórnio 23 ° 26 ′ (23,43 °) S círculo Antártico 66 ° 34 ′ (66,57 °) S
O plano da órbita da Terra em torno do Sol é chamado de eclíptica , e o plano perpendicular ao eixo de rotação da Terra é o plano equatorial. O ângulo entre a eclíptica e o plano equatorial é chamado de inclinação axial, obliquidade ou inclinação da eclíptica, e é convencionalmente denotado por i . A latitude dos círculos tropicais é igual a i e a latitude dos círculos polares é seu complemento (90 ° - i ). O eixo de rotação varia lentamente ao longo do tempo e os valores fornecidos aqui são os da época atual . A variação de tempo é discutida mais detalhadamente no artigo sobre inclinação axial .
A figura mostra a geometria de uma seção transversal do plano perpendicular à eclíptica e através dos centros da Terra e do Sol no solstício de dezembro , quando o Sol está acima em algum ponto do Trópico de Capricórnio . As latitudes polares sul abaixo do Círculo Antártico são diurnas, enquanto as latitudes polares norte acima do Círculo Ártico são noturnas. A situação se inverte no solstício de junho, quando o Sol está alto no Trópico de Câncer. Somente em latitudes entre os dois trópicos é possível que o Sol esteja diretamente acima (no zênite ).
Em projeções de mapas, não existe uma regra universal sobre como os meridianos e paralelos devem aparecer. Os exemplos abaixo mostram os paralelos nomeados (como linhas vermelhas) na projeção de Mercator comumente usada e na projeção de Mercator Transversal . No primeiro, os paralelos são horizontais e os meridianos são verticais, enquanto no último não há uma relação exata dos paralelos e meridianos com a horizontal e a vertical: ambos são curvas complicadas.
| Mercator normal | Transverse Mercator | |||
|---|---|---|---|---|
|
\ |
Latitude no elipsóide
Elipsoides
Em 1687, Isaac Newton publicou o Philosophiæ Naturalis Principia Mathematica , no qual ele provou que um corpo fluido rotativo autogravitante em equilíbrio assume a forma de um elipsóide oblato . (Este artigo usa o termo elipsóide em vez do termo mais antigo esferóide .) O resultado de Newton foi confirmado por medições geodésicas no século XVIII. (Consulte Arco meridiano .) Um elipsóide achatado é a superfície tridimensional gerada pela rotação de uma elipse em torno de seu eixo mais curto (eixo menor). "Elipsóide de revolução oblato" é abreviado para 'elipsóide' no restante deste artigo. (Os elipsóides que não têm um eixo de simetria são denominados triaxiais.)
Muitos elipsóides de referência diferentes foram usados na história da geodésia . Em dias pré-satélite, eles foram concebidos para dar um bom ajuste ao geóide sobre a área limitada de um levantamento, mas, com o advento do GPS , tornou-se natural usar elipsóides de referência (como WGS84 ) com centro no centro de massa da Terra e eixo menor alinhado ao eixo de rotação da Terra. Esses elipsóides geocêntricos estão geralmente a 100 m (330 pés) do geóide. Visto que a latitude é definida em relação a um elipsóide, a posição de um determinado ponto é diferente em cada elipsóide: não se pode especificar exatamente a latitude e longitude de um elemento geográfico sem especificar o elipsóide usado. Muitos mapas mantidos por agências nacionais são baseados em elipsóides mais antigos, portanto, é preciso saber como os valores de latitude e longitude são transformados de um elipsóide para outro. Os aparelhos GPS incluem software para realizar transformações de datum que ligam o WGS84 ao elipsóide de referência local com sua grade associada.
A geometria do elipsóide
A forma de um elipsóide de revolução é determinada pela forma da elipse que é girada em torno de seu eixo menor (mais curto). Dois parâmetros são obrigatórios. Um é invariavelmente o raio equatorial, que é o semi-eixo maior , a . O outro parâmetro é geralmente (1) o raio polar ou semi-eixo menor , b ; ou (2) o (primeiro) achatamento , f ; ou (3) a excentricidade , e . Esses parâmetros não são independentes: eles estão relacionados por
Muitos outros parâmetros (ver elipse , elipsóide ) aparecem no estudo da geodésia, geofísica e projeções cartográficas, mas todos podem ser expressos em termos de um ou dois membros do conjunto a , b , f e e . Ambos f e e são pequenos e freqüentemente aparecem em expansões em série nos cálculos; eles são da ordem1/298e 0,0818 respectivamente. Os valores de vários elipsóides são fornecidos na Figura da Terra . Elipsóides de referência são geralmente definidos pelo semieixo maior e o achatamento inverso ,1/f. Por exemplo, os valores de definição para o elipsóide WGS84 , usado por todos os dispositivos GPS, são
- a (raio equatorial):6 378 137 0,0 m exactamente
- 1/f (achatamento inverso): 298,257 223 563 exatamente
do qual são derivados
- b (raio polar):6 356 752 ,3142 m
- e 2 (excentricidade ao quadrado):0,006 694 379 990 14
A diferença entre o semi-eixo maior e o semi-eixo menor é de cerca de 21 km (13 milhas) e como fração do semi-eixo maior é igual ao achatamento; em um monitor de computador, o elipsóide pode ter o tamanho de 300 por 299 pixels. Isso dificilmente seria distinguível de uma esfera de 300 por 300 pixels, então as ilustrações geralmente exageram o achatamento.
Latitudes geodésicas e geocêntricas
A gratícula no elipsóide é construída exatamente da mesma maneira que na esfera. A normal em um ponto na superfície de um elipsóide não passa pelo centro, exceto para pontos no equador ou nos pólos, mas a definição de latitude permanece inalterada como o ângulo entre a normal e o plano equatorial. A terminologia para latitude deve ser mais precisa, distinguindo:
- Latitude geodésica: o ângulo entre o plano normal e o plano equatorial. A notação padrão nas publicações em inglês é ϕ . Esta é a definição assumida quando a palavra latitude é usada sem qualificação. A definição deve vir acompanhada de uma especificação do elipsóide.
- Latitude geocêntrica: o ângulo entre o raio (do centro ao ponto na superfície) e o plano equatorial. (Figura abaixo ). Não há notação padrão: exemplos de vários textos incluem θ , ψ , q , ϕ ′ , ϕ c , ϕ g . Este artigo usa θ .
- Latitude esférica: o ângulo entre a superfície de referência normal e esférica e o plano equatorial.
- A latitude geográfica deve ser usada com cuidado. Alguns autores a utilizam como sinônimo de latitude geodésica, enquanto outros a utilizam como alternativa à latitude astronômica .
- Latitude (não qualificado) normalmente deve se referir à latitude geodésica.
A importância de especificar o datum de referência pode ser ilustrada por um exemplo simples. No elipsóide de referência para WGS84, o centro da Torre Eiffel tem uma latitude geodésica de 48 ° 51 ′ 29 ″ N, ou 48,8583 ° N e longitude de 2 ° 17 ′ 40 ″ E ou 2,2944 ° E. As mesmas coordenadas do datum ED50 definem um ponto no solo a 140 metros (460 pés) de distância da torre. Uma pesquisa na web pode produzir vários valores diferentes para a latitude da torre; o elipsóide de referência raramente é especificado.
Distância do meridiano
O comprimento de um grau de latitude depende da figura da Terra assumida.
Distância do meridiano na esfera
Na esfera, a normal passa pelo centro e a latitude ( ϕ ) é, portanto, igual ao ângulo subtendido no centro pelo arco do meridiano do equador ao ponto em questão. Se a distância do meridiano é denotada por m ( ϕ ), então
onde R denota o raio médio da Terra. R é igual a 6.371 km ou 3.959 milhas. Nenhuma precisão maior é apropriada para R, uma vez que resultados de alta precisão requerem um modelo elipsóide. Com este valor para R, o comprimento do meridiano de 1 grau de latitude na esfera é 111,2 km (69,1 milhas estatutárias) (60,0 milhas náuticas). O comprimento de 1 minuto de latitude é 1,853 km (1,151 milhas náuticas) (1,00 milhas náuticas), enquanto o comprimento de 1 segundo de latitude é 30,8 m ou 101 pés (ver milhas náuticas ).
Distância meridiana no elipsóide
No arco de meridiano e em textos padrão, é mostrado que a distância ao longo de um meridiano da latitude ϕ ao equador é dada por ( ϕ em radianos)
onde M ( ϕ ) é o raio meridional de curvatura .
A distância de um quarto do meridiano do equador ao pólo é
Para WGS84 esta distância é10 001 0,965 729 km .
A avaliação da integral da distância meridiana é central para muitos estudos em geodésia e projeção de mapas. Ele pode ser avaliado expandindo a integral pela série binomial e integrando termo a termo: consulte o arco meridiano para obter detalhes. O comprimento do arco meridiano entre duas latitudes dadas é dado substituindo os limites da integral pelas latitudes em questão. O comprimento de um pequeno arco meridiano é dado por
| Δ1 lat |
Δ1 longa |
|
|---|---|---|
| 0 ° | 110.574 km | 111.320 km |
| 15 ° | 110,649 km | 107.550 km |
| 30 ° | 110,852 km | 96,486 km |
| 45 ° | 111,132 km | 78.847 km |
| 60 ° | 111,412 km | 55,800 km |
| 75 ° | 111,618 km | 28,902 km |
| 90 ° | 111,694 km | 0,000 km |
Quando a diferença de latitude é de 1 grau, correspondendo a π/180 radianos, a distância do arco é sobre
A distância em metros (correta para 0,01 metro) entre as latitudes - 0,5 graus e + 0,5 graus no esferóide WGS84 é
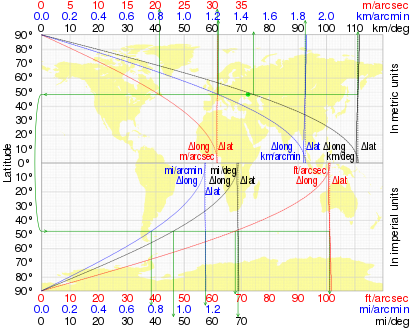
A variação desta distância com a latitude (no WGS84 ) é mostrada na tabela junto com o comprimento de um grau de longitude (distância leste-oeste):
Uma calculadora para qualquer latitude é fornecida pela National Geospatial-Intelligence Agency (NGA) do governo dos EUA .
O gráfico a seguir ilustra a variação de um grau de latitude e um grau de longitude com a latitude.
Latitudes auxiliares
Existem seis latitudes auxiliares que têm aplicações em problemas especiais em geodésia, geofísica e teoria das projeções cartográficas:
- Latitude geocêntrica
- Latitude paramétrica (ou reduzida)
- Latitude retificadora
- Latitude autálica
- Latitude conforme
- Latitude isométrica
Todas as definições fornecidas nesta seção se referem a localizações no elipsóide de referência, mas as duas primeiras latitudes auxiliares, como a latitude geodésica, podem ser estendidas para definir um sistema de coordenadas geográficas tridimensional , conforme discutido abaixo . As latitudes restantes não são usadas dessa maneira; eles são usados apenas como construções intermediárias em projeções de mapa do elipsóide de referência para o plano ou em cálculos de geodésicas no elipsóide. Seus valores numéricos não são de interesse. Por exemplo, ninguém precisaria calcular a latitude autálica da Torre Eiffel.
As expressões abaixo fornecem as latitudes auxiliares em termos da latitude geodésica, o semieixo maior, a , e a excentricidade, e . (Para inversos, veja abaixo .) As formas fornecidas são, além das variantes notacionais, aquelas na referência padrão para projeções de mapas, a saber "Projeções de mapas: um manual de trabalho" por JP Snyder. Derivações dessas expressões podem ser encontradas em Adams e publicações online de Osborne e Rapp.
Latitude geocêntrica
A latitude geocêntrica é o ângulo entre o plano equatorial e o raio do centro a um ponto na superfície. A relação entre a latitude geocêntrica ( θ ) e a latitude geodésica ( ϕ ) é derivada nas referências acima como
As latitudes geodésicas e geocêntricas são iguais no equador e nos pólos, mas em outras latitudes elas diferem por alguns minutos de arco. Tomando o valor da excentricidade quadrada como 0,0067 (depende da escolha do elipsóide), a diferença máxima de pode ser mostrada como sendo cerca de 11,5 minutos de arco em uma latitude geodésica de aproximadamente 45 ° 6 ′.
Latitude paramétrica (ou reduzida)
A latitude paramétrica ou reduzida , β , é definida pelo raio traçado a partir do centro do elipsóide até aquele ponto Q na esfera circundante (de raio a ) que é a projeção paralela ao eixo da Terra de um ponto P no elipsóide em latitude ϕ . Foi introduzido por Legendre e Bessel que resolveram problemas para geodésicas no elipsóide, transformando-os em um problema equivalente para geodésicas esféricas usando esta latitude menor. A notação de Bessel, u ( ϕ ) , também é usada na literatura atual. A latitude paramétrica está relacionada à latitude geodésica por:
O nome alternativo surge da parametrização da equação da elipse que descreve uma seção do meridiano. Em termos de coordenadas cartesianas p , a distância do eixo menor, ez , a distância acima do plano equatorial, a equação da elipse é:
As coordenadas cartesianas do ponto são parametrizadas por
Cayley sugeriu o termo latitude paramétrica devido à forma dessas equações.
A latitude paramétrica não é usada na teoria de projeções de mapas. Sua aplicação mais importante é na teoria da geodésica elipsóide, ( Vincenty , Karney).
Latitude retificadora
A latitude retificadora , μ , é a distância do meridiano escalada de modo que seu valor nos pólos seja igual a 90 graus ouπ/2 radianos:
onde está a distância do meridiano do equador a uma latitude ϕ (ver arco de meridiano )
e o comprimento do quadrante meridiano do equador ao pólo (a distância polar ) é
Usando a latitude de retificação para definir uma latitude em uma esfera de raio
define uma projeção do elipsóide para a esfera de forma que todos os meridianos tenham comprimento verdadeiro e escala uniforme. A esfera pode então ser projetada para o plano com uma projeção equirretangular para dar uma projeção dupla do elipsóide para o plano de modo que todos os meridianos tenham comprimento verdadeiro e escala de meridiano uniforme. Um exemplo do uso da latitude retificadora é a projeção cônica equidistante . (Snyder, Seção 16). A latitude retificadora também é de grande importância na construção da projeção de Mercator Transversal .
Latitude autálica
A latitude autálica (grego para mesma área ), ξ , fornece uma transformação que preserva a área em uma esfera.
Onde
e
e o raio da esfera é considerado como
Um exemplo do uso da latitude autálica é a projeção cônica de área igual de Albers .
Latitude conforme
A latitude conforme , χ , fornece uma transformação que preserva o ângulo ( conforme ) para a esfera.
onde gd ( x ) é a função Gudermanniana . (Veja também a projeção de Mercator .)
A latitude conforme define uma transformação do elipsóide para uma esfera de raio arbitrário, de modo que o ângulo de intersecção entre quaisquer duas linhas no elipsóide seja o mesmo que o ângulo correspondente na esfera (de modo que a forma dos pequenos elementos seja bem preservada) . Uma outra transformação conforme da esfera para o plano dá uma projeção conformada dupla do elipsóide para o plano. Esta não é a única maneira de gerar tal projeção conforme. Por exemplo, a versão 'exata' da projeção Transverse Mercator no elipsóide não é uma projeção dupla. (No entanto, envolve uma generalização da latitude conforme para o plano complexo).
Latitude isométrica
A latitude isométrica , ψ , é usada no desenvolvimento das versões elipsoidais da projeção Mercator normal e da projeção Mercator transversal . O nome "isométrico" surge do fato de que em qualquer ponto do elipsóide incrementos iguais de ψ e longitude λ dão origem a deslocamentos de distância iguais ao longo dos meridianos e paralelos, respectivamente. A gratícula definida pelas linhas de ψ constante e λ constante divide a superfície do elipsóide em uma malha de quadrados (de tamanho variável). A latitude isométrica é zero no equador, mas diverge rapidamente da latitude geodésica, tendendo ao infinito nos pólos. A notação convencional é dada em Snyder (página 15):
Para a projeção de Mercator normal (no elipsóide) esta função define o espaçamento dos paralelos: se o comprimento do equador na projeção é E (unidades de comprimento ou pixels), então a distância, y , de um paralelo de latitude ϕ de o equador é
A latitude isométrica ψ está intimamente relacionada à latitude conforme χ :
Fórmulas e séries inversas
As fórmulas nas seções anteriores fornecem a latitude auxiliar em termos da latitude geodésica. As expressões para as latitudes geocêntricas e paramétricas podem ser invertidas diretamente, mas isso é impossível nos quatro casos restantes: as latitudes retificadora, autálica, conformada e isométrica. Existem dois métodos de procedimento.
- O primeiro é uma inversão numérica da equação definidora para todo e qualquer valor particular da latitude auxiliar. Os métodos disponíveis são iteração de ponto fixo e descoberta de raiz de Newton-Raphson .
- Ao converter de isométrico ou conforme para geodésico, duas iterações de Newton-Raphson fornecem precisão de precisão dupla .
- A outra abordagem, mais útil, é expressar a latitude auxiliar como uma série em termos da latitude geodésica e então inverter a série pelo método de reversão de Lagrange . Essas séries são apresentadas por Adams, que usa as expansões da série de Taylor e fornece coeficientes em termos de excentricidade. Osborne deriva séries em ordem arbitrária usando o pacote de álgebra computacional Maxima e expressa os coeficientes em termos de excentricidade e achatamento. O método da série não é aplicável à latitude isométrica e deve-se encontrar a latitude conforme em uma etapa intermediária.
Comparação numérica de latitudes auxiliares
O gráfico à direita mostra a diferença entre a latitude geodésica e as latitudes auxiliares além da latitude isométrica (que diverge para o infinito nos pólos) para o caso do elipsóide WGS84. As diferenças mostradas no gráfico estão em minutos de arco. No hemisfério norte (latitudes positivas), θ ≤ χ ≤ μ ≤ ξ ≤ β ≤ ϕ ; no hemisfério sul (latitudes negativas), as desigualdades se invertem, com igualdade no equador e nos pólos. Embora o gráfico pareça simétrico em cerca de 45 °, os mínimos das curvas na verdade estão entre 45 ° 2 ′ e 45 ° 6 ′. Alguns pontos de dados representativos são fornecidos na tabela abaixo. As latitudes conformadas e geocêntricas são quase indistinguíveis, fato que foi explorado na época das calculadoras manuais para agilizar a construção de projeções cartográficas.
Para a primeira ordem no achatamento f , as latitudes auxiliares podem ser expressas como ζ = ϕ - Cf sen 2 ϕ onde a constante C assume os valores [ 1 ⁄ 2 , 2 ⁄ 3 , 3 ⁄ 4 , 1, 1] para ζ = [ β , ξ , μ , χ , θ ].
| ϕ | Paramétrico β - ϕ |
Authalic ξ - ϕ |
Retificando μ - ϕ |
Conformal χ - ϕ |
Geocêntrico θ - ϕ |
|---|---|---|---|---|---|
| 0 ° | 0,00 ′ | 0,00 ′ | 0,00 ′ | 0,00 ′ | 0,00 ′ |
| 15 ° | -2,88 ′ | -3,84 ′ | -4,32 ′ | -5,76 ′ | -5,76 ′ |
| 30 ° | -5,00 ′ | -6,66 ′ | -7,49 ′ | -9,98 ′ | -9,98 ′ |
| 45 ° | -5,77 ′ | -7,70 ′ | -8,66 ′ | -11,54 ′ | -11,55 ′ |
| 60 ° | -5,00 ′ | -6,67 ′ | -7,51 ′ | -10,01 ′ | -10,02 ′ |
| 75 ° | -2,89 ′ | -3,86 ′ | -4,34 ′ | -5,78 ′ | -5,79 ′ |
| 90 ° | 0,00 ′ | 0,00 ′ | 0,00 ′ | 0,00 ′ | 0,00 ′ |
Latitude e sistemas de coordenadas
A latitude geodésica, ou qualquer uma das latitudes auxiliares definidas no elipsóide de referência, constitui com a longitude um sistema de coordenadas bidimensional naquele elipsóide. Para definir a posição de um ponto arbitrário, é necessário estender esse sistema de coordenadas em três dimensões. Três latitudes são usadas desta forma: as latitudes geodésicas, geocêntricas e paramétricas são usadas em coordenadas geodésicas, coordenadas polares esféricas e coordenadas elipsoidais, respectivamente.
Coordenadas geodésicas
Em um ponto arbitrário P considere a linha PN que é normal ao elipsóide de referência. As coordenadas geodésicas P ( ɸ , λ , h ) são a latitude e longitude do ponto N no elipsóide e a distância PN . Esta altura difere da altura acima do geóide ou de uma altura de referência, como aquela acima do nível médio do mar em um local especificado. A direção de PN também será diferente da direção de uma linha de prumo vertical. A relação dessas diferentes alturas requer conhecimento da forma do geóide e também do campo gravitacional da Terra.
Coordenadas polares esféricas
A latitude geocêntrica θ é o complemento do ângulo polar θ ′ em coordenadas polares esféricas convencionais em que as coordenadas de um ponto são P ( r , θ ′, λ ) onde r é a distância de P do centro O , θ ′ é o ângulo entre o vetor do raio e o eixo polar e λ é a longitude. Como a normal em um ponto geral do elipsóide não passa pelo centro, é claro que os pontos P ' da normal, que possuem a mesma latitude geodésica, terão latitudes geocêntricas diferentes. Sistemas esféricos de coordenadas polares são usados na análise do campo gravitacional.
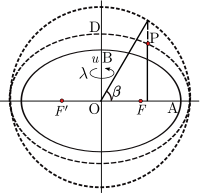
Coordenadas elipsoidais
A latitude paramétrica também pode ser estendida a um sistema de coordenadas tridimensional. Para um ponto P que não está no elipsóide de referência (semieixos OA e OB ), construa um elipsóide auxiliar que seja confocal (mesmos focos F , F ′ ) com o elipsóide de referência: a condição necessária é que o produto ae do semieixo maior e a excentricidade é a mesma para ambos os elipsóides. Seja u o semi-eixo menor ( OD ) do elipsóide auxiliar. Além disso, seja β a latitude paramétrica de P no elipsóide auxiliar. O conjunto ( u , β , λ ) define as coordenadas elipsoidais , também conhecidas como coordenadas elipsoidais-harmônicas . Essas coordenadas são a escolha natural em modelos do campo gravitacional para um corpo elipsoidal em rotação. O acima se aplica a um elipsóide biaxial (um esferóide, como nas coordenadas esferoidais oblatas ); para uma generalização, consulte as coordenadas elipsoidais triaxiais .
Coordenar conversões
As relações entre os sistemas de coordenadas acima e também as coordenadas cartesianas não são apresentadas aqui. A transformação entre as coordenadas geodésicas e cartesianas pode ser encontrada em Conversão de coordenadas geográficas . A relação dos polares cartesianos e esféricos é dada no sistema de coordenadas esféricas . A relação das coordenadas cartesianas e elipsoidais é discutida em Torge.
Latitude astronômica
Latitude astronômica ( Φ ) é o ângulo entre o plano equatorial e a direção vertical verdadeira em um ponto da superfície. A verdadeira vertical, a direção de um fio de prumo , é também a direção da gravidade (a resultante da aceleração gravitacional (baseada na massa) e da aceleração centrífuga ) naquela latitude. A latitude astronômica é calculada a partir dos ângulos medidos entre o zênite e as estrelas cuja declinação é conhecida com precisão.
Em geral, a verdadeira vertical em um ponto da superfície não coincide exatamente com a normal para o elipsóide de referência ou com a normal para o geóide. O ângulo entre os normais astronômicos e geodésicos é chamado de deflexão vertical e geralmente tem alguns segundos de arco, mas é importante na geodésia. A razão pela qual ele difere do normal para o geóide é porque o geóide é uma forma teórica idealizada "ao nível médio do mar". Os pontos na superfície real da terra estão geralmente acima ou abaixo desta superfície geóide idealizada e aqui a verdadeira vertical pode variar ligeiramente. Além disso, a verdadeira vertical em um ponto em um momento específico é influenciada por forças de maré, que o geóide teórico calcula em média.
A latitude astronômica não deve ser confundida com declinação , a coordenada que os astrônomos usam de forma semelhante para especificar a posição angular das estrelas ao norte / sul do equador celestial (ver as coordenadas equatoriais ), nem com a latitude eclíptica , a coordenada que os astrônomos usam para especificar a posição angular das estrelas ao norte / sul da eclíptica (veja as coordenadas da eclíptica ).
Veja também
- Altitude ( nível médio do mar )
- American Practical Navigator do Bowditch
- Direção cardinal
- Círculo de latitude
- Colatitude
- Declinação na esfera celestial
- Projeto de Confluência de Grau
- Geodésia
- Datum geodésico
- Sistema de coordenadas geográficas
- Distância geográfica
- Latitude geomagnética
- Geotagging
- Distância do grande círculo
- História da latitude .
- Latitudes de cavalo
- Serviço Latitude Internacional
- Lista de países por latitude
- Longitude
- Código de área natural
- Navegação
- Ordens de magnitude (comprimento)
- Sistema Geodésico Mundial
Referências
Notas de rodapé
Citações
links externos
- Servidor de nomes GEONets , acesso ao banco de dados da National Geospatial-Intelligence Agency (NGA) de nomes de características geográficas estrangeiras.
- Recursos para determinar sua latitude e longitude
- Converta graus decimais em graus, minutos, segundos - Informações sobre a conversão de decimal em sexagesimal
- Converta graus decimais em graus, minutos, segundos
- Cálculo da distância com base na latitude e longitude - versão JavaScript
- Pesquisa Latitude do século 16
- Determinação da latitude por Francis Drake na costa da Califórnia em 1579



























![{\ displaystyle {\ begin {alinhados} q (\ phi) & = {\ frac {\ left (1-e ^ {2} \ right) \ sin \ phi} {1-e ^ {2} \ sin ^ { 2} \ phi}} - {\ frac {1-e ^ {2}} {2e}} \ ln \ left ({\ frac {1-e \ sin \ phi} {1 + e \ sin \ phi}} \ right) \\ [2pt] & = {\ frac {\ left (1-e ^ {2} \ right) \ sin \ phi} {1-e ^ {2} \ sin ^ {2} \ phi}} + {\ frac {1-e ^ {2}} {e}} \ tanh ^ {- 1} (e \ sin \ phi) \ end {alinhado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b256b2b2f95ca49231dfb329dd724cdbd2de7d1)


![{\ displaystyle {\ begin {alinhado} \ chi (\ phi) & = 2 \ tan ^ {- 1} \ left [\ left ({\ frac {1+ \ sin \ phi} {1- \ sin \ phi} } \ right) \ left ({\ frac {1-e \ sin \ phi} {1 + e \ sin \ phi}} \ right) ^ {e} \ right] ^ {\ frac {1} {2}} - {\ frac {\ pi} {2}} \\ [2pt] & = 2 \ tan ^ {- 1} \ left [\ tan \ left ({\ frac {\ phi} {2}} + {\ frac {\ pi} {4}} \ right) \ left ({\ frac {1-e \ sin \ phi} {1 + e \ sin \ phi}} \ right) ^ {\ frac {e} {2}} \ right] - {\ frac {\ pi} {2}} \\ [2pt] & = \ tan ^ {- 1} \ left [\ sinh \ left (\ sinh ^ {- 1} (\ tan \ phi) -e \ tanh ^ {- 1} (e \ sin \ phi) \ right) \ right] \\ & = \ operatorname {gd} \ left [\ operatorname {gd} ^ {- 1} (\ phi) -e \ tanh ^ {- 1} (e \ sin \ phi) \ right] \ end {alinhado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eea5beec16e6a78772ab9d8ffd9123b9ae6e89e0)
![{\ displaystyle {\ begin {alinhados} \ psi (\ phi) & = \ ln \ left [\ tan \ left ({\ frac {\ pi} {4}} + {\ frac {\ phi} {2}} \ right) \ right] + {\ frac {e} {2}} \ ln \ left [{\ frac {1-e \ sin \ phi} {1 + e \ sin \ phi}} \ right] \\ & = \ sinh ^ {- 1} (\ tan \ phi) -e \ tanh ^ {- 1} (e \ sin \ phi) \\ & = \ operatorname {gd} ^ {- 1} (\ phi) -e \ tanh ^ {- 1} (e \ sin \ phi). \ end {alinhado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2999bd8461a831ee601ecad69062c5b30adec5f)