Diagrama Dynkin - Dynkin diagram

Grupos de mentiras
Grupos clássicos
Grupos de Lie simples Clássico A n B n C n D n Excepcional G 2 F 4 E 6 E 7 E 8
Outros grupos de Lie Círculo Lorentz Poincaré Grupo Conformal Difeomorfismo Laço Euclidiana
Álgebras de Lie
Álgebra de Lie semisimples
Teoria da representação
Grupos de mentiras em física
Cientistas Sophus Lie Henri Poincaré Wilhelm Killing Élie Cartan Hermann Weyl Claude Chevalley Harish-Chandra Armand Borel
Glossário Tabela de grupos de Lie
v t e

No campo matemático da teoria de Lie , um diagrama Dynkin , nomeado para Eugene Dynkin , é um tipo de gráfico com algumas arestas duplicadas ou triplicadas (desenhado como uma linha dupla ou tripla). Os diagramas Dynkin surgem na classificação de álgebras de Lie semisimples sobre campos algebraicamente fechados , na classificação de grupos de Weyl e outros grupos de reflexão finitos e em outros contextos. Várias propriedades do diagrama Dynkin (como se ele contém várias arestas ou suas simetrias) correspondem a características importantes da álgebra de Lie associada.

Diagramas Finite Dynkin

Diagramas Dynkin afins (estendidos)

O termo "diagrama Dynkin" pode ser ambíguo. Em alguns casos, os diagramas Dynkin são assumidos como direcionados , caso em que eles correspondem a sistemas de raízes e álgebras de Lie semi-simples, enquanto em outros casos eles são considerados não direcionados , caso em que correspondem a grupos de Weyl. Neste artigo, "diagrama Dynkin" significa diagrama Dynkin direcionado , e diagramas Dynkin não direcionados serão explicitamente nomeados.

Classificação de álgebras de Lie semisimples

O interesse fundamental nos diagramas Dynkin é que eles classificam álgebras de Lie semisimples sobre campos algebraicamente fechados . Classificam-se tais álgebras de Lie por meio de seu sistema de raiz , que pode ser representado por um diagrama Dynkin. Em seguida, classifica-se os diagramas Dynkin de acordo com as restrições que eles devem satisfazer, conforme descrito a seguir.

Abaixar a direção nas bordas do grafo corresponde a substituir um sistema de raiz pelo grupo de reflexão finito que ele gera, o chamado grupo de Weyl , e assim os diagramas Dynkin não direcionados classificam os grupos de Weyl.

Eles têm a seguinte correspondência para as álgebras de Lie associadas a grupos clássicos sobre os números complexos:

• ${\ displaystyle A_ {n}}$: , a álgebra de Lie linear especial .${\ displaystyle {\ mathfrak {sl}} _ {n + 1}}$
• ${\ displaystyle B_ {n}}$: , a álgebra de Lie ortogonal especial de dimensão ímpar .${\ displaystyle {\ mathfrak {so}} _ {2n + 1}}$
• ${\ displaystyle C_ {n}}$: , a álgebra de Lie simplética .${\ displaystyle {\ mathfrak {sp}} _ {2n}}$
• ${\ displaystyle D_ {n}}$: , a álgebra de Lie ortogonal especial de dimensão par ( ).${\ displaystyle {\ mathfrak {so}} _ {2n}}$${\ displaystyle n> 1}$

Para os grupos excepcionais, os nomes da álgebra de Lie e do diagrama Dynkin associado coincidem.

Classificações relacionadas

Os diagramas Dynkin podem ser interpretados como classificando muitos objetos distintos e relacionados, e a notação "A _n , B _n , ..." é usada para se referir a todas essas interpretações, dependendo do contexto; essa ambigüidade pode ser confusa.

A classificação central é que uma álgebra de Lie simples possui um sistema radicular, ao qual está associado um diagrama Dynkin (orientado); todos os três podem ser referidos como B _n , por exemplo.

O diagrama Dynkin não orientado é uma forma de diagrama de Coxeter e corresponde ao grupo de Weyl, que é o grupo finito de reflexão associado ao sistema radicular. Assim, B _n pode se referir ao diagrama não orientado (um tipo especial de diagrama de Coxeter), ao grupo de Weyl (um grupo de reflexão concreto) ou ao grupo abstrato de Coxeter.

Embora o grupo Weyl seja abstratamente isomórfico ao grupo Coxeter, um isomorfismo específico depende de uma escolha ordenada de raízes simples. Da mesma forma, enquanto a notação do diagrama Dynkin é padronizada, o diagrama de Coxeter e a notação de grupo são variados e às vezes concordam com a notação do diagrama Dynkin e às vezes não.

Por último, às vezes os objetos associados são referidos pela mesma notação, embora isso nem sempre possa ser feito regularmente. Exemplos incluem:

• A raiz da estrutura gerada pelo sistema de raízes, como no E ₈ treliça . Isso é definido naturalmente, mas não um-para-um - por exemplo, A ₂ e G ₂ geram a rede hexagonal .
• Um poliepítopo associadas - por exemplo Gosset 4 ₂₁ poliepítopo pode ser referido como "o E ₈ poliepítopo", como seus vértices são derivados a partir da E ₈ sistema radicular e que tem o E ₈ grupo de Coxeter como grupo de simetria.
• Uma forma quadrática ou variedade associada - por exemplo, a variedade E ₈ tem forma de interseção dada pela rede E ₈ .

Essas últimas notações são usadas principalmente para objetos associados a diagramas excepcionais - objetos associados aos diagramas regulares (A, B, C, D) em vez disso têm nomes tradicionais.

O índice ( n ) é igual ao número de nós no diagrama, o número de raízes simples em uma base, a dimensão da rede de raiz e extensão do sistema de raiz, o número de geradores do grupo de Coxeter e a classificação da álgebra de Lie. No entanto, n não é igual à dimensão do módulo de definição (uma representação fundamental ) da álgebra de Lie - o índice no diagrama Dynkin não deve ser confundido com o índice na álgebra de Lie. Por exemplo, corresponde a que atua naturalmente no espaço de 9 dimensões, mas tem classificação 4 como uma álgebra de Lie. ${\ displaystyle B_ {4}}$${\ displaystyle {\ mathfrak {so}} _ {2 \ cdot 4 + 1} = {\ mathfrak {so}} _ {9},}$

Os diagramas Dynkin simplesmente entrelaçados , aqueles sem arestas múltiplas (A, D, E) classificam muitos outros objetos matemáticos; veja a discussão na classificação ADE .

Exemplo: ${\ displaystyle A_ {2}}$

O sistema raiz.${\ displaystyle A_ {2}}$

Por exemplo, o símbolo pode se referir a: ${\ displaystyle A_ {2}}$

• O diagrama Dynkin com 2 nós conectados,, que também pode ser interpretado como um diagrama de Coxeter .
• O sistema radicular com 2 raízes simples em um ângulo (120 graus).${\ displaystyle 2 \ pi / 3}$
• A álgebra de Lie de classificação 2.${\ displaystyle {\ mathfrak {sl}} _ {2 + 1} = {\ mathfrak {sl}} _ {3}}$
• O grupo Weyl de simetrias das raízes (reflexos no hiperplano ortogonal às raízes), isomorfo ao grupo simétrico (de ordem 6).${\ displaystyle S_ {3}}$
• O resumo do grupo Coxeter , apresentado por geradores e relações,${\ displaystyle \ left \ langle r_ {1}, r_ {2} \ mid (r_ {1}) ^ {2} = (r_ {2}) ^ {2} = (r_ {i} r_ {j}) ^ {3} = 1 \ direita \ rangle.}$

Construção de sistemas de raiz

Considere um sistema radicular , considerado reduzido e integral (ou "cristalográfico"). Em muitas aplicações, este sistema raiz surgirá de uma álgebra de Lie semisimples . Let Ser um conjunto de raízes simples positivas . Em seguida, construímos um diagrama a partir do seguinte. Forme um gráfico com um vértice para cada elemento de . Em seguida, insira arestas entre cada par de vértices de acordo com a seguinte receita. Se as raízes correspondentes aos dois vértices são ortogonais, não há aresta entre os vértices. Se o ângulo entre as duas raízes for 120 graus, colocamos uma aresta entre os vértices. Se o ângulo for 135 graus, colocamos duas arestas, e se o ângulo for 150 graus, colocamos três arestas. (Esses quatro casos exaurem todos os ângulos possíveis entre pares de raízes simples positivas.) Finalmente, se houver alguma aresta entre um determinado par de vértices, nós os decoramos com uma seta apontando do vértice correspondente à raiz mais longa até o vértice correspondente a o mais curto. (A flecha é omitida se as raízes tiverem o mesmo comprimento.) Pensar na flecha como um sinal de "maior que" deixa claro para onde ela deve ir. Os diagramas Dynkin levam a uma classificação dos sistemas radiculares. Os ângulos e as proporções de comprimento entre as raízes estão relacionados . Assim, as bordas para raízes não ortogonais podem alternativamente ser descritas como uma borda para uma razão de comprimento de 1, duas bordas para uma razão de comprimento de e três bordas para uma razão de comprimento de . (Não há arestas quando as raízes são ortogonais, independentemente da proporção do comprimento.) ${\ displaystyle \ Delta}$${\ displaystyle \ Delta}$${\ displaystyle \ Delta}$${\ displaystyle {\ sqrt {2}}}$${\ displaystyle {\ sqrt {3}}}$

No sistema radicular, mostrado à direita, as raízes são marcadas e formam uma base. Como essas duas raízes estão em um ângulo de 120 graus (com uma proporção de comprimento de 1), o diagrama Dynkin consiste em dois vértices conectados por uma única aresta:${\ displaystyle A_ {2}}$${\ displaystyle \ alpha}$${\ displaystyle \ beta}$.

Restrições

Os diagramas Dynkin devem satisfazer certas restrições; estes são essencialmente aqueles satisfeitos por diagramas finitos de Coxeter-Dynkin , junto com uma restrição cristalográfica adicional.

Conexão com diagramas de Coxeter

Os diagramas Dynkin estão intimamente relacionados aos diagramas de Coxeter de grupos de Coxeter finitos , e a terminologia costuma ser confundida.

Os diagramas Dynkin diferem dos diagramas de Coxeter de grupos finitos em dois aspectos importantes:

Parcialmente dirigido

Os diagramas Dynkin são parcialmente direcionados - qualquer aresta múltipla (em termos de Coxeter, rotulada com "4" ou acima) tem uma direção (uma seta apontando de um nó para o outro); portanto, os diagramas Dynkin têm mais dados do que o diagrama de Coxeter subjacente (gráfico não direcionado).

No nível dos sistemas de raízes, a direção corresponde a apontar para o vetor mais curto; as arestas marcadas com "3" não têm direção porque os vetores correspondentes devem ter comprimentos iguais. (Cuidado: alguns autores invertem essa convenção, com a seta apontando para o vetor mais longo.)

Restrição cristalográfica

Os diagramas Dynkin devem satisfazer uma restrição adicional, ou seja, que os únicos rótulos de borda permitidos são 2, 3, 4 e 6, uma restrição não compartilhada pelos diagramas de Coxeter, portanto, nem todo diagrama de Coxeter de um grupo finito vem de um diagrama de Dynkin.

No nível dos sistemas de raízes, isso corresponde ao teorema da restrição cristalográfica , já que as raízes formam uma rede.

Uma outra diferença, que é apenas estilística, é que os diagramas Dynkin são convencionalmente desenhados com bordas duplas ou triplas entre os nós (para p  = 4, 6), ao invés de uma borda marcada com " p ".

O termo "diagrama Dynkin" às vezes se refere ao gráfico direcionado , às vezes ao gráfico não direcionado. Para precisão, neste artigo "diagrama Dynkin" significará direcionado, e o gráfico não direcionado subjacente será chamado de "diagrama Dynkin não direcionado". Então, os diagramas Dynkin e diagramas Coxeter podem ser relacionados da seguinte forma:

Isso significa que os diagramas de Coxeter de grupos finitos correspondem a grupos de pontos gerados por reflexões, enquanto os diagramas de Dynkin devem satisfazer uma restrição adicional correspondente ao teorema de restrição cristalográfica e que os diagramas de Coxeter não são direcionados, enquanto os diagramas de Dynkin são (parcialmente) direcionados.

Os objetos matemáticos correspondentes classificados pelos diagramas são:

O espaço em branco no canto superior direito, correspondendo a gráficos direcionados com gráfico não direcionado subjacente a qualquer diagrama de Coxeter (de um grupo finito), pode ser definido formalmente, mas é pouco discutido e não parece admitir uma interpretação simples em termos de objetos matemáticos de interesse.

Existem mapas naturais - de diagramas Dynkin a diagramas Dynkin não direcionados; respectivamente, dos sistemas de raiz aos grupos Weyl associados - e à direita - dos diagramas Dynkin não direcionados aos diagramas de Coxeter; respectivamente de grupos Weyl para grupos finitos de Coxeter.

O mapa descendente é on (por definição), mas não um-para-um, já que os diagramas B _n e C _{n são} mapeados para o mesmo diagrama não direcionado, com o diagrama de Coxeter e o grupo de Weyl resultantes, portanto, às vezes denotados como BC _n .

O mapa certo é simplesmente uma inclusão - diagramas Dynkin não direcionados são casos especiais de diagramas de Coxeter, e grupos de Weyl são casos especiais de grupos Coxeter finitos - e não são, já que nem todo diagrama de Coxeter é um diagrama Dynkin não direcionado (os diagramas perdidos sendo H ₃ , H ₄ e I ₂ ( p ) para p  = 5  p  ≥ 7), e correspondentemente nem todo grupo finito de Coxeter é um grupo de Weyl.

Isomorfismos

Os isomorfismos excepcionais de diagramas Dynkin conectados.

Os diagramas Dynkin são numerados convencionalmente para que a lista não seja redundante: for for for for e começando em As famílias podem, no entanto, ser definidas para n inferior , produzindo isomorfismos excepcionais de diagramas e isomorfismos excepcionais correspondentes de álgebras de Lie e grupos de Lie associados. ${\ displaystyle n \ geq 1}$${\ displaystyle A_ {n},}$ ${\ displaystyle n \ geq 2}$${\ displaystyle B_ {n},}$ ${\ displaystyle n \ geq 3}$${\ displaystyle C_ {n},}$ ${\ displaystyle n \ geq 4}$${\ displaystyle D_ {n},}$${\ displaystyle E_ {n}}$${\ displaystyle n = 6.}$

Trivialmente, pode-se começar as famílias em ou que são todas isomórficas, pois há um diagrama vazio único e um diagrama único de 1 nó. Os outros isomorfismos de diagramas Dynkin conectados são: ${\ displaystyle n = 0}$${\ displaystyle n = 1,}$

• ${\ displaystyle A_ {1} \ cong B_ {1} \ cong C_ {1}}$
• ${\ displaystyle B_ {2} \ cong C_ {2}}$
• ${\ displaystyle D_ {2} \ cong A_ {1} \ times A_ {1}}$
• ${\ displaystyle D_ {3} \ cong A_ {3}}$
• ${\ displaystyle E_ {3} \ cong A_ {1} \ times A_ {2}}$
• ${\ displaystyle E_ {4} \ cong A_ {4}}$
• ${\ displaystyle E_ {5} \ cong D_ {5}}$

Esses isomorfismos correspondem ao isomorfismo de álgebras de Lie simples e semisimples, que também correspondem a certos isomorfismos de formas de grupo de Lie destas. Eles também adicionam contexto à família E _n .

Automorfismos

O diagrama Dynkin mais simétrico é D ₄ , que dá origem à trialidade .

Além do isomorfismo entre diferentes diagramas, alguns diagramas também possuem autoisomorfismos ou " automorfismos ". Os automorfismos do diagrama correspondem aos automorfismos externos da álgebra de Lie, o que significa que o grupo de automorfismos externos Out = Aut / Inn é igual ao grupo dos automorfismos do diagrama.

Os diagramas que possuem automorfismos não triviais são A _n ( ), D _n ( ) e E ₆ . Em todos esses casos, exceto para D ₄ , há um único automorfismo não trivial (Out = C ₂ , o grupo cíclico de ordem 2), enquanto para D ₄ , o grupo de automorfismo é o grupo simétrico de três letras ( S ₃ , ordem 6) - este fenômeno é conhecido como " trialidade ". Acontece que todos esses automorfismos de diagrama podem ser realizados como simetrias euclidianas de como os diagramas são convencionalmente desenhados no plano, mas isso é apenas um artefato de como eles são desenhados, e não uma estrutura intrínseca. ${\ displaystyle n> 1}$${\ displaystyle n> 1}$

A _n .

Para A _n , o automorfismo do diagrama está invertendo o diagrama, que é uma linha. Os nós do diagrama indexam os pesos fundamentais , que (para A _{n −1} ) são para , e o automorfismo do diagrama corresponde à dualidade. Realizado como a álgebra de Lie, o automorfismo externo pode ser expresso como transposta negativa , que é como a dupla atos de representação. ${\ displaystyle \ bigwedge ^ {i} C ^ {n}}$${\ displaystyle i = 1, \ dots, n}$${\ displaystyle \ bigwedge ^ {i} C ^ {n} \ mapsto \ bigwedge ^ {ni} C ^ {n}.}$${\ displaystyle {\ mathfrak {sl}} _ {n + 1},}$${\ displaystyle T \ mapsto -T ^ {\ mathrm {T}}}$

D _n .

Para D _n , o automorfismo do diagrama está alternando os dois nós no final do Y e corresponde à alternância das duas representações de spin quirais . Realizado como a álgebra de Lie, o automorfismo externo pode ser expresso como conjugação por uma matriz em O (2 n ) com determinante -1. Quando n = 3, tem-se então que seus automorfismos concordam, enquanto está desconectado, e o automorfismo corresponde à comutação dos dois nós. ${\ displaystyle {\ mathfrak {so}} _ {2n},}$${\ displaystyle \ mathrm {D} _ {3} \ cong \ mathrm {A} _ {3},}$${\ displaystyle \ mathrm {D} _ {2} \ cong \ mathrm {A} _ {1} \ times \ mathrm {A} _ {1}}$

Para D ₄ , a representação fundamental é isomórfica às duas representações de spin, e o grupo simétrico resultante em três letras ( S ₃ ou, alternativamente, o grupo diédrico de ordem 6, Dih ₃ ) corresponde a automorfismos da álgebra de Lie e automorfismos de o diagrama.

E ₆ .

O grupo de automorfismo de E ₆ corresponde à reversão do diagrama e pode ser expresso usando álgebras de Jordan .

Os diagramas desconectados, que correspondem a álgebras de Lie semi simples, podem ter automorfismos de troca de componentes do diagrama.

Na característica 2, a seta em F ₄ pode ser ignorada, gerando um automorfismo de diagrama adicional e grupos Suzuki-Ree correspondentes .

Na característica positiva, há "automorfismos de diagrama" adicionais - grosso modo, na característica p, às vezes é permitido ignorar a seta em ligações de multiplicidade p no diagrama Dynkin ao tomar automorfismos de diagrama. Assim, na característica 2 há um automorfismo de ordem 2 de e de F ₄ , enquanto na característica 3 há um automorfismo de ordem 2 de G ₂ . Mas não se aplica a todas as circunstâncias: por exemplo, tais automorfismos não precisam surgir como automorfismos do grupo algébrico correspondente, mas sim no nível de pontos avaliados em um corpo finito. ${\ displaystyle \ mathrm {B} _ {2} \ cong \ mathrm {C} _ {2}}$

Construção de grupos de Lie por meio de automorfismos de diagrama

Os automorfismos do diagrama, por sua vez, geram grupos de Lie adicionais e grupos do tipo de Lie , que são de importância central na classificação de grupos simples finitos.

A construção do grupo de Chevalley de grupos de Lie em termos de seu diagrama Dynkin não produz alguns dos grupos clássicos, a saber, os grupos unitários e os grupos ortogonais não divididos . Os grupos de Steinberg constroem os grupos unitários ² A _n , enquanto os outros grupos ortogonais são construídos como ² D _n , onde em ambos os casos isso se refere à combinação de um automorfismo de diagrama com um automorfismo de campo. Isso também produz grupos de Lie exóticos adicionais ² E ₆ e ³ D ₄ , o último apenas definido sobre campos com um automorfismo de ordem 3.

Os automorfismos de diagrama adicionais em característica positiva geram os grupos Suzuki-Ree , ² B ₂ , ² F ₄ e ² G ₂ .

Dobrando

Dobras do grupo Finite Coxeter.

Dobras de grupo Affine Coxeter, com três convenções de nomenclatura: primeiro, o conjunto estendido original; o segundo usado no contexto de gráficos de quiver ; e o último por Victor Kac para álgebras de Lie afins torcidas .

Um diagrama Dynkin (simplesmente entrelaçado) (finito ou afim ) que tem uma simetria (satisfazendo uma condição, abaixo) pode ser quociente pela simetria, produzindo um novo diagrama, geralmente multiplamente entrelaçado, com o processo chamado de dobramento (devido à maioria das simetrias sendo 2 vezes). No nível das álgebras de Lie, isso corresponde a tomar a subálgebra invariante sob o grupo de automorfismo externo, e o processo pode ser definido puramente com referência aos sistemas de raiz, sem usar diagramas. Além disso, todos os diagramas de múltiplos laços (finitos ou infinitos) podem ser obtidos dobrando um diagrama de laços simples.

A única condição no automorfismo para que o dobramento seja possível é que nós distintos do grafo na mesma órbita (sob o automorfismo) não devem ser conectados por uma aresta; no nível dos sistemas radiculares, as raízes na mesma órbita devem ser ortogonais. No nível dos diagramas, isso é necessário, caso contrário, o diagrama de quociente terá um loop, devido à identificação de dois nós, mas com uma aresta entre eles, e os loops não são permitidos nos diagramas Dynkin.

Os nós e arestas do diagrama quociente ("dobrado") são as órbitas dos nós e arestas do diagrama original; as bordas são únicas, a menos que duas bordas incidentes sejam mapeadas para a mesma borda (principalmente em nós de valência maiores que 2) - um "ponto de ramificação" do mapa, caso em que o peso é o número de bordas incidentes, e a seta aponta para o nó no qual eles são incidentes - "o ponto de ramificação é mapeado para o ponto não homogêneo". Por exemplo, em D ₄ dobramento para G ₂ , a aresta em G ₂ aponta da classe dos 3 nós externos (valência 1), para a classe do nó central (valência 3).

As dobras dos diagramas finitos são:

• ${\ displaystyle A_ {2n-1} \ a C_ {n}}$

(A automorphism de A _{2 n} não produzir uma dobragem porque as médias de dois nós estão ligados por uma aresta, mas na mesma órbita.)

• ${\ displaystyle D_ {n + 1} \ para B_ {n}}$
• ${\ displaystyle D_ {4} \ a G_ {2}}$(se estiver em quociente por todo o grupo ou em 3 ciclos, além de 3 formas diferentes, se estiver em quociente por uma involução)${\ displaystyle D_ {4} \ a B_ {3}}$
• ${\ displaystyle E_ {6} \ a F_ {4}}$

Existem dobras semelhantes para diagramas afins, incluindo:

• ${\ displaystyle {\ tilde {A}} _ {2n-1} \ a {\ tilde {C}} _ ​​{n}}$
• ${\ displaystyle {\ tilde {D}} _ {n + 1} \ para {\ tilde {B}} _ {n}}$
• ${\ displaystyle {\ tilde {D}} _ {4} \ to {\ tilde {G}} _ {2}}$
• ${\ displaystyle {\ tilde {E}} _ {6} \ to {\ tilde {F}} _ {4}}$

A noção de dobramentos também pode ser aplicada de forma mais geral aos diagramas de Coxeter - notavelmente, pode-se generalizar quocientes permitidos de diagramas de Dynkin para H _n e I ₂ ( p ). Geometricamente, isso corresponde a projeções de politopos uniformes . Notavelmente, qualquer diagrama Dynkin simplesmente atado pode ser dobrado para I ₂ ( h ), onde h é o número de Coxeter , que corresponde geometricamente à projeção para o plano de Coxeter .

O dobramento pode ser aplicado para reduzir as questões sobre álgebras de Lie (semisimples) a questões sobre álgebras simplesmente entrelaçadas, junto com um automorfismo, que pode ser mais simples do que tratar álgebras multiplamente entrelaçadas diretamente; isso pode ser feito na construção das álgebras de Lie semisimples, por exemplo. Veja Math Overflow: Folding by Automorphisms para uma discussão mais aprofundada.

Outros mapas de diagramas

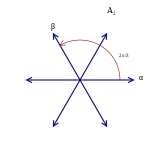Um sistema de 2 raízes

Sistema de raiz G 2

Alguns mapas adicionais de diagramas têm interpretações significativas, conforme detalhado a seguir. No entanto, nem todos os mapas de sistemas raiz surgem como mapas de diagramas.

Por exemplo, existem duas inclusões de sistemas radiculares de A ₂ em G ₂ , ou como as seis raízes longas ou as seis raízes curtas. No entanto, os nós no diagrama G ₂ correspondem a uma raiz longa e uma raiz curta, enquanto os nós no diagrama A ₂ correspondem a raízes de igual comprimento e, portanto, este mapa de sistemas de raiz não pode ser expresso como um mapa dos diagramas .

Algumas inclusões de sistemas de raízes podem ser expressas como um diagrama sendo um subgráfico induzido de outro, significando "um subconjunto de nós, com todas as arestas entre eles". Isso ocorre porque a eliminação de um nó de um diagrama Dynkin corresponde à remoção de uma raiz simples de um sistema raiz, o que resulta em um sistema raiz de classificação inferior. Em contraste, remover uma aresta (ou alterar a multiplicidade de uma aresta) enquanto deixa os nós inalterados corresponde a alterar os ângulos entre as raízes, o que não pode ser feito sem alterar todo o sistema radicular. Assim, pode-se remover nós de forma significativa, mas não arestas. Remover um nó de um diagrama conectado pode produzir um diagrama conectado (álgebra de Lie simples), se o nó for uma folha, ou um diagrama desconectado (álgebra de Lie semisimples, mas não simples), com dois ou três componentes (o último para D _n e E _n ). No nível das álgebras de Lie, essas inclusões correspondem às álgebras de sub-Lie.

Os subgráficos máximos são os seguintes; os subgráficos relacionados por um automorfismo de diagrama são rotulados como "conjugado":

• A _{n +1} : A _n , de 2 formas conjugadas.
• B _{n +1} : A _n , B _n .
• C _{n 1} : Um _n , C _n .
• D _{n +1} : A _n (2 formas conjugadas), D _n .
• E _{n +1} : A _n , D _n , E _n .
  • Para E ₆ , dois deles coincidem: e são conjugados.${\ displaystyle \ mathrm {D} _ {5} \ cong \ mathrm {E} _ {5}}$
• F ₄ : B ₃ , C ₃ .
• G ₂ : A ₁ , de 2 formas não conjugadas (como raiz longa ou raiz curta).

Finalmente, a dualidade dos diagramas corresponde a inverter a direção das setas, se houver: B _n e C _n são duais, enquanto F ₄ e G ₂ são autoduais, assim como os diagramas ADE simplesmente atados.

Simplesmente atado

Os diagramas Dynkin simplesmente entrelaçados classificam diversos objetos matemáticos; isso é chamado de classificação ADE .

Um diagrama Dynkin sem arestas múltiplas é chamado simplesmente atado , assim como a álgebra de Lie e o grupo de Lie correspondentes. Esses são os diagramas e os fenômenos que esses diagramas classificam são chamados de classificação ADE . Nesse caso, os diagramas Dynkin coincidem exatamente com os diagramas de Coxeter, pois não há arestas múltiplas. ${\ displaystyle A_ {n}, D_ {n}, E_ {n}}$

Diagramas Satake

Os diagramas Dynkin classificam álgebras de Lie semissimples complexas . Álgebras de Lie semissimples reais podem ser classificadas como formas reais de álgebras de Lie semissimples complexas, e são classificadas por diagramas de Satake , que são obtidos a partir do diagrama Dynkin rotulando alguns vértices de preto (preenchido) e conectando alguns outros vértices em pares por setas, de acordo com certas regras.

História

Eugene Dynkin .

Os diagramas de Dynkin são nomeados em homenagem a Eugene Dynkin , que os usou em dois artigos (1946, 1947), simplificando a classificação de álgebras de Lie semisimples; veja ( Dynkin 2000 ) . Quando Dynkin deixou a União Soviética em 1976, o que na época era considerado equivalente a traição, os matemáticos soviéticos foram orientados a se referir a "diagramas de raízes simples" em vez de usar seu nome. erro harv: sem alvo: CITEREFDynkin2000 ( ajuda )

Grafos não direcionados foram usados ​​anteriormente por Coxeter (1934) para classificar grupos de reflexão , onde os nós correspondiam a reflexões simples; os gráficos foram então usados ​​(com informações de comprimento) por Witt (1941) em referência a sistemas de raízes, com os nós correspondendo a raízes simples, como são usados ​​hoje. Dynkin então os usou em 1946 e 1947, reconhecendo Coxeter e Witt em seu artigo de 1947.

Convenções

Os diagramas Dynkin foram desenhados de várias maneiras; a convenção seguida aqui é comum, com ângulos de 180 ° nos nós de valência 2, ângulos de 120 ° nos nós de valência 3 de D _n e ângulos de 90 ° / 90 ° / 180 ° nos nós de valência 3 de E _n , com multiplicidade indicado por 1, 2 ou 3 arestas paralelas e o comprimento da raiz indicado pelo desenho de uma seta na aresta para orientação. Além da simplicidade, um benefício adicional dessa convenção é que os automorfismos do diagrama são realizados por isometrias euclidianas dos diagramas.

A convenção alternativa inclui escrever um número pela aresta para indicar multiplicidade (comumente usado em diagramas de Coxeter), escurecimento dos nós para indicar o comprimento da raiz ou usar ângulos de 120 ° em 2 nós de valência para tornar os nós mais distintos.

Também existem convenções sobre a numeração dos nós. A convenção moderna mais comum foi desenvolvida na década de 1960 e é ilustrada em ( Bourbaki 1968 ).

Diagramas Dynkin Rank 2

Os diagramas Dynkin são equivalentes às matrizes Cartan generalizadas , conforme mostrado nesta tabela de diagramas Dynkin de classificação 2 com suas matrizes Cartan 2 x 2 correspondentes .

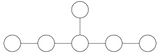
Para a classificação 2, a forma da matriz de Cartan é:

${\ displaystyle A = \ left [{\ begin {matrix} 2 & a_ {12} \\ a_ {21} & 2 \ end {matrix}} \ right]}$

Um diagrama com várias arestas corresponde aos elementos da matriz Cartan não-diagonal -a ₂₁ , -a ₁₂ , com o número de arestas desenhadas igual a max (-a ₂₁ , -a ₁₂ ) e uma seta apontando para os elementos não-unidade.

Uma matriz Cartan generalizada é uma matriz quadrada tal que: ${\ displaystyle A = (a_ {ij})}$

1. Para entradas diagonais ,.${\ displaystyle a_ {ii} = 2}$
2. Para entradas não diagonais ,.${\ displaystyle a_ {ij} \ leq 0}$
3. ${\ displaystyle a_ {ij} = 0}$ se e apenas se ${\ displaystyle a_ {ji} = 0}$

A matriz de Cartan determina se o grupo é do tipo finito (se for uma matriz Definida Positiva , ou seja, todos os valores próprios são positivos), do tipo afim (se não for definido positivo, mas semidefinido positivo, ou seja, todos os valores próprios são não negativo), ou de tipo indefinido . O tipo indefinido frequentemente é subdividido, por exemplo, um grupo Coxeter é Lorentziano se tiver um autovalor negativo e todos os outros autovalores forem positivos. Além disso, fontes múltiplas referem-se a grupos Coxeter hiperbólicos , mas existem várias definições não equivalentes para este termo. Na discussão abaixo, os grupos Coxeter hiperbólicos são um caso especial de Lorentzian, satisfazendo uma condição extra. Para a classificação 2, todas as matrizes de Cartan determinantes negativos correspondem ao grupo Coxeter hiperbólico. Mas, em geral, a maioria das matrizes determinantes negativas não são hiperbólicas nem Lorentzianas.

Os ramos finitos têm (-a ₂₁ , -a ₁₂ ) = (1,1), (2,1), (3,1), e os ramos afins (com um determinante zero) têm (-a ₂₁ , -a ₁₂ ) = (2,2) ou (4,1).

Diagramas Dynkin Rank 2

Nome do grupo	Diagrama Dynkin			Matriz cartan		Ordem de simetria	Grupo 3 relacionado com simplesmente atado
	(Padrão) gráfico multi-gumes	Gráfico valorizado 1	Gráfico de Coxeter 2	${\ displaystyle \ left [{\ begin {matrix} 2 & a_ {12} \\ a_ {21} & 2 \ end {matrix}} \ right]}$	Determinante (4-a 21 * a 12 )
Finito (Determinante> 0)
A 1 xA 1				${\ displaystyle \ left [{\ begin {smallmatrix} 2 & 0 \\ 0 & 2 \ end {smallmatrix}} \ right]}$	4	2
A 2 (não direcionado)				${\ displaystyle \ left [{\ begin {smallmatrix} 2 e -1 \\ - 1 e 2 \ end {smallmatrix}} \ right]}$	3	3
B 2				${\ displaystyle \ left [{\ begin {smallmatrix} 2 e -2 \\ - 1 e 2 \ end {smallmatrix}} \ right]}$	2	4	${\ displaystyle {A} _ {3}}$
C 2				${\ displaystyle \ left [{\ begin {smallmatrix} 2 e -1 \\ - 2 e 2 \ end {smallmatrix}} \ right]}$	2	4	${\ displaystyle {A} _ {3}}$
BC 2 (não direcionado)				${\ displaystyle \ left [{\ begin {smallmatrix} 2 & - {\ sqrt {2}} \\ - {\ sqrt {2}} & 2 \ end {smallmatrix}} \ right]}$	2	4
G 2				${\ displaystyle \ left [{\ begin {smallmatrix} 2 e -1 \\ - 3 e 2 \ end {smallmatrix}} \ right]}$	1	6	${\ displaystyle {D} _ {4}}$
G 2 (não direcionado)				${\ displaystyle \ left [{\ begin {smallmatrix} 2 & - {\ sqrt {3}} \\ - {\ sqrt {3}} & 2 \ end {smallmatrix}} \ right]}$	1	6
Afim (Determinante = 0)
A 1 (1)				${\ displaystyle \ left [{\ begin {smallmatrix} 2 e -2 \\ - 2 e 2 \ end {smallmatrix}} \ right]}$	0	∞	${\ displaystyle {\ tilde {A}} _ {3}}$
A 2 (2)				${\ displaystyle \ left [{\ begin {smallmatrix} 2 e -1 \\ - 4 e 2 \ end {smallmatrix}} \ right]}$	0	∞	${\ displaystyle {\ tilde {D}} _ {4}}$
Hiperbólico (Determinante <0)
				${\ displaystyle \ left [{\ begin {smallmatrix} 2 e -1 \\ - 5 e 2 \ end {smallmatrix}} \ right]}$	-1	-
				${\ displaystyle \ left [{\ begin {smallmatrix} 2 e -2 \\ - 3 e 2 \ end {smallmatrix}} \ right]}$	-2	-
				${\ displaystyle \ left [{\ begin {smallmatrix} 2 e -1 \\ - 6 e 2 \ end {smallmatrix}} \ right]}$	-2	-
				${\ displaystyle \ left [{\ begin {smallmatrix} 2 e -1 \\ - 7 & 2 \ end {smallmatrix}} \ right]}$	-3	-
				${\ displaystyle \ left [{\ begin {smallmatrix} 2 e -2 \\ - 4 e 2 \ end {smallmatrix}} \ right]}$	-4	-
				${\ displaystyle \ left [{\ begin {smallmatrix} 2 e -1 \\ - 8 e 2 \ end {smallmatrix}} \ right]}$	-4	-
				${\ displaystyle \ left [{\ begin {smallmatrix} 2 e -3 \\ - 3 e 2 \ end {smallmatrix}} \ right]}$	-5	-
				${\ displaystyle \ left [{\ begin {smallmatrix} 2 & -b \\ - a & 2 \ end {smallmatrix}} \ right]}$	4-ab <0	-
Nota 1 : Para grupos hiperbólicos, (a 12 * a 21 > 4), o estilo de múltiplas camadas é abandonado em favor de uma rotulação explícita (a 21 , a 12 ) na borda. Eles geralmente não são aplicados a gráficos finitos e afins. Nota 2 : Para grupos não direcionados, os diagramas de Coxeter são intercambiáveis. Eles geralmente são rotulados por sua ordem de simetria, com ordem 3 implícita sem rótulo. Nota 3 : Muitos grupos com várias arestas podem ser obtidos de um grupo simplesmente atado de classificação superior aplicando uma operação de dobra adequada .

Diagramas Finite Dynkin

Gráficos Finite Dynkin com 1 a 9 nós

Classificação	Grupos de Lie clássica				Grupos de Lie excepcionais
	${\ displaystyle {A} _ {1+}}$	${\ displaystyle {B} _ {2+}}$	${\ displaystyle {C} _ {2+}}$	${\ displaystyle {D} _ {2+}}$	${\ displaystyle {E} _ {3-8}}$	${\ displaystyle {G} _ {2}}$ / ${\ displaystyle {F} _ {4}}$
1	A 1
2	A 2	B 2	C 2 = B 2	D 2 = A 1 A 1		G 2
3	A 3	B 3	C 3	D 3 = A 3	E 3 = A 2 A 1
4	A 4	B 4	C 4	D 4	E 4 = A 4	F 4
5	A 5	B 5	C 5	D 5	E 5 = D 5
6	A 6	B 6	C 6	D 6	E 6
7	A 7	B 7	C 7	D 7	E 7
8	A 8	B 8	C 8	D 8	E 8
9	A 9	B 9	C 9	D 9
10+	..	..	..	..

Diagramas Affine Dynkin

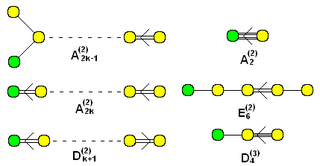
Existem extensões dos diagramas Dynkin, nomeadamente os diagramas Dynkin afins ; estes classificam as matrizes Cartan de álgebras de Lie afins . Estes são classificados em ( Kac 1994 , Capítulo 4, pp. 47– ) , especificamente listados em ( Kac 1994 , pp. 53–55 ) . Os diagramas afins são denotados como ou onde X é a letra do diagrama finito correspondente, e o expoente depende da série de diagramas afins em que estão. O primeiro deles, são mais comuns, e são chamados de diagramas Dynkin estendidos e denotados com um til , e também às vezes marcado com um + sobrescrito. como em . As séries (2) e (3) são chamadas de diagramas afins torcidos . erro harv: sem alvo: CITEREFKac1994 ( ajuda )erro harv: sem alvo: CITEREFKac1994 ( ajuda )${\ displaystyle X_ {l} ^ {(1)}, X_ {l} ^ {(2)},}$${\ displaystyle X_ {l} ^ {(3)},}$${\ displaystyle X_ {l} ^ {(1)},}$${\ displaystyle {\ tilde {A}} _ {5} = A_ {5} ^ {(1)} = A_ {5} ^ {+}}$

Consulte o gerador de diagramas Dynkin para diagramas.

O conjunto de diagramas Dynkin afins estendidos, com nós adicionados em verde ( para e para ) ${\ displaystyle n \ geq 3}$${\ displaystyle B_ {n}}$${\ displaystyle n \ geq 4}$${\ displaystyle D_ {n}}$

Formas afins "torcidas" são nomeadas com (2) ou (3) sobrescritos. (O subscrito k sempre conta o número de nós amarelos no gráfico, ou seja, o número total de nós menos 1.)

Aqui estão todos os gráficos Dynkin para grupos afins de até 10 nós. Os gráficos Dynkin estendidos são fornecidos como famílias ~ , o mesmo que os gráficos finitos acima, com um nó adicionado. Outras variações de gráfico direcionado são fornecidas com um valor sobrescrito (2) ou (3), representando dobras de grupos de ordem superior. Eles são categorizados como diagramas afins torcidos .

Gráficos Dynkin afins conectados de até (2 a 10 nós)
(agrupados como gráficos não direcionados)

Classificação	${\ displaystyle {\ tilde {A}} _ {1+}}$	${\ displaystyle {\ tilde {B}} _ {3+}}$	${\ displaystyle {\ tilde {C}} _ ​​{2+}}$	${\ displaystyle {\ tilde {D}} _ {4+}}$	E / F / G
2	${\ displaystyle {\ tilde {A}} _ {1}}$ ou ${\ displaystyle {A} _ {1} ^ {(1)}}$		${\ displaystyle {A} _ {2} ^ {(2)}}$:
3	${\ displaystyle {\ tilde {A}} _ {2}}$ ou ${\ displaystyle {A} _ {2} ^ {(1)}}$		${\ displaystyle {\ tilde {C}} _ ​​{2}}$ ou ${\ displaystyle {C} _ {2} ^ {(1)}}$ ${\ displaystyle {D} _ {5} ^ {(2)}}$: ${\ displaystyle {A} _ {4} ^ {(2)}}$:		${\ displaystyle {\ tilde {G}} _ {2}}$ ou ${\ displaystyle {G} _ {2} ^ {(1)}}$ ${\ displaystyle {D} _ {4} ^ {(3)}}$
4	${\ displaystyle {\ tilde {A}} _ {3}}$ ou ${\ displaystyle {A} _ {3} ^ {(1)}}$	${\ displaystyle {\ tilde {B}} _ {3}}$ ou ${\ displaystyle {B} _ {3} ^ {(1)}}$ ${\ displaystyle {A} _ {5} ^ {(2)}}$:	${\ displaystyle {\ tilde {C}} _ ​​{3}}$ ou ${\ displaystyle {C} _ {3} ^ {(1)}}$ ${\ displaystyle {D} _ {6} ^ {(2)}}$: ${\ displaystyle {A} _ {6} ^ {(2)}}$:
5	${\ displaystyle {\ tilde {A}} _ {4}}$ ou ${\ displaystyle {A} _ {4} ^ {(1)}}$	${\ displaystyle {\ tilde {B}} _ {4}}$ ou ${\ displaystyle {B} _ {4} ^ {(1)}}$ ${\ displaystyle {A} _ {7} ^ {(2)}}$:	${\ displaystyle {\ tilde {C}} _ ​​{4}}$ ou ${\ displaystyle {C} _ {4} ^ {(1)}}$ ${\ displaystyle {D} _ {7} ^ {(2)}}$: ${\ displaystyle {A} _ {8} ^ {(2)}}$:	${\ displaystyle {\ tilde {D}} _ {4}}$ ou ${\ displaystyle {D} _ {4} ^ {(1)}}$	${\ displaystyle {\ tilde {F}} _ {4}}$ ou ${\ displaystyle {F} _ {4} ^ {(1)}}$ ${\ displaystyle {E} _ {6} ^ {(2)}}$
6	${\ displaystyle {\ tilde {A}} _ {5}}$ ou ${\ displaystyle {A} _ {5} ^ {(1)}}$	${\ displaystyle {\ tilde {B}} _ {5}}$ ou ${\ displaystyle {B} _ {5} ^ {(1)}}$ ${\ displaystyle {A} _ {9} ^ {(2)}}$:	${\ displaystyle {\ tilde {C}} _ ​​{5}}$ ou ${\ displaystyle {C} _ {5} ^ {(1)}}$ ${\ displaystyle {D} _ {8} ^ {(2)}}$: ${\ displaystyle {A} _ {10} ^ {(2)}}$:	${\ displaystyle {\ tilde {D}} _ {5}}$ ou ${\ displaystyle {D} _ {5} ^ {(1)}}$
7	${\ displaystyle {\ tilde {A}} _ {6}}$ ou ${\ displaystyle {A} _ {6} ^ {(1)}}$	${\ displaystyle {\ tilde {B}} _ {6}}$ ou ${\ displaystyle {B} _ {6} ^ {(1)}}$ ${\ displaystyle {A} _ {11} ^ {(2)}}$:	${\ displaystyle {\ tilde {C}} _ ​​{6}}$ ou ${\ displaystyle {C} _ {6} ^ {(1)}}$ ${\ displaystyle {D} _ {9} ^ {(2)}}$: ${\ displaystyle {A} _ {12} ^ {(2)}}$:	${\ displaystyle {\ tilde {D}} _ {6}}$ ou ${\ displaystyle {D} _ {6} ^ {(1)}}$	${\ displaystyle {\ tilde {E}} _ {6}}$ ou ${\ displaystyle {E} _ {6} ^ {(1)}}$
8	${\ displaystyle {\ tilde {A}} _ {7}}$ ou ${\ displaystyle {A} _ {7} ^ {(1)}}$	${\ displaystyle {\ tilde {B}} _ {7}}$ ou ${\ displaystyle {B} _ {7} ^ {(1)}}$ ${\ displaystyle {A} _ {13} ^ {(2)}}$:	${\ displaystyle {\ tilde {C}} _ ​​{7}}$ ou ${\ displaystyle {C} _ {7} ^ {(1)}}$ ${\ displaystyle {D} _ {10} ^ {(2)}}$: ${\ displaystyle {A} _ {14} ^ {(2)}}$:	${\ displaystyle {\ tilde {D}} _ {7}}$ ou ${\ displaystyle {D} _ {7} ^ {(1)}}$	${\ displaystyle {\ tilde {E}} _ {7}}$ ou ${\ displaystyle {E} _ {7} ^ {(1)}}$
9	${\ displaystyle {\ tilde {A}} _ {8}}$ ou ${\ displaystyle {A} _ {8} ^ {(1)}}$	${\ displaystyle {\ tilde {B}} _ {8}}$ ou ${\ displaystyle {B} _ {8} ^ {(1)}}$ ${\ displaystyle {A} _ {15} ^ {(2)}}$:	${\ displaystyle {\ tilde {C}} _ ​​{8}}$ ou ${\ displaystyle {C} _ {8} ^ {(1)}}$ ${\ displaystyle {D} _ {11} ^ {(2)}}$: ${\ displaystyle {A} _ {16} ^ {(2)}}$:	${\ displaystyle {\ tilde {D}} _ {8}}$ ou ${\ displaystyle {D} _ {8} ^ {(1)}}$	${\ displaystyle {\ tilde {E}} _ {8}}$ ou ${\ displaystyle {E} _ {8} ^ {(1)}}$
10	${\ displaystyle {\ tilde {A}} _ {9}}$ ou ${\ displaystyle {A} _ {9} ^ {(1)}}$	${\ displaystyle {\ tilde {B}} _ {9}}$ ou ${\ displaystyle {B} _ {9} ^ {(1)}}$ ${\ displaystyle {A} _ {17} ^ {(2)}}$:	${\ displaystyle {\ tilde {C}} _ ​​{9}}$ ou ${\ displaystyle {C} _ {9} ^ {(1)}}$ ${\ displaystyle {D} _ {12} ^ {(2)}}$: ${\ displaystyle {A} _ {18} ^ {(2)}}$:	${\ displaystyle {\ tilde {D}} _ {9}}$ ou ${\ displaystyle {D} _ {9} ^ {(1)}}$
11	...	...	...	...

Diagramas de Dynkin hiperbólico e superior

O conjunto de gráficos Dynkin hiperbólicos compactos e não compactos foi enumerado. Todos os gráficos hiperbólicos de classificação 3 são compactos. Os diagramas Dynkin hiperbólicos compactos existem até a classificação 5 e os gráficos hiperbólicos não compactos existem até a classificação 10.

Diagramas Dynkin hiperbólicos compactos

Não compacto (formulários estendidos demais)

Algumas notações usadas na física teórica , como a teoria M , usam um "+" sobrescrito para grupos estendidos em vez de um "~" e isso permite que grupos de extensões maiores sejam definidos.

1. Os diagramas Dynkin estendidos (afins) recebem "+" e representam um nó adicionado. (O mesmo que "~")
2. Os diagramas Dynkin superestendidos (hiperbólicos) são fornecidos "^" ou "++" e representam dois nós adicionados.
3. Os diagramas Dynkin muito estendidos com 3 nós adicionados recebem "+++".

Alguns exemplos de diagramas Dynkin superestendidos (hiperbólicos)

Classificação	${\ displaystyle {AE} _ {n}}$= A n-2 (1) ^	${\ displaystyle {BE} _ {n}}$= B n-2 (1) ^ ${\ displaystyle {CE} _ {n}}$	C n-2 (1) ^	${\ displaystyle {DE} _ {n}}$= D n-2 (1) ^	E / F / G
3	${\ displaystyle {AE} _ {3}}$:
4	${\ displaystyle {AE} _ {4}}$:		C 2 (1) ^ A 4 (2) '^ A 4 (2) ^ D 3 (2) ^		G 2 (1) ^ D 4 (3) ^
5	${\ displaystyle {AE} _ {5}}$:	${\ displaystyle {BE} _ {5}}$ ${\ displaystyle {CE} _ {5}}$	C 3 (1) ^ A 6 (2) ^ A 6 (2) '^ D 5 (2) ^
6	${\ displaystyle {AE} _ {6}}$	${\ displaystyle {BE} _ {6}}$ ${\ displaystyle {CE} _ {6}}$	C 4 (1) ^ A 8 (2) ^ A 8 (2) '^ D 7 (2) ^	${\ displaystyle {DE} _ {6}}$	F 4 (1) ^ E 6 (2) ^
7	${\ displaystyle {AE} _ {7}}$	${\ displaystyle {BE} _ {7}}$ ${\ displaystyle {CE} _ {7}}$		${\ displaystyle {DE} _ {7}}$
8	${\ displaystyle {AE} _ {8}}$	${\ displaystyle {BE} _ {8}}$ ${\ displaystyle {CE} _ {8}}$		${\ displaystyle {DE} _ {8}}$	E 6 (1) ^
9	${\ displaystyle {AE} _ {9}}$	${\ displaystyle {BE} _ {9}}$ ${\ displaystyle {CE} _ {9}}$		${\ displaystyle {DE} _ {9}}$	E 7 (1) ^
10		${\ displaystyle {BE} _ {10}}$ ${\ displaystyle {CE} _ {10}}$		${\ displaystyle {DE} _ {10}}$	${\ displaystyle {E} _ {10}}$= E 8 (1) ^

238 grupos hiperbólicos (compactos e não compactos)

Os 238 grupos hiperbólicos (compactos e não compactos) de classificação são nomeados e listados para cada classificação. ${\ displaystyle n \ geq 3}$${\ displaystyle H_ {i} ^ {(n)}}$${\ displaystyle i = 1,2,3 ...}$

Muito extenso

Grupos muito estendidos são grupos de Lorentz , definidos pela adição de três nós aos grupos finitos. O E ₈ , E ₇ , E ₆ , F ₄ e G ₂ oferecem seis séries terminando como grupos muito estendidos. Outras séries estendidas não mostradas podem ser definidas a partir de A _n , B _n , C _n e D _n , como séries diferentes para cada n . O determinante da matriz de Cartan associada determina onde a série muda de finita (positiva) para afim (zero) para um grupo hiperbólico não compacto (negativo) e terminando como um grupo de Lorentz que pode ser definido com o uso de uma dimensão semelhante ao tempo , e é usado em teoria M .

Série estendida de classificação 2

Finito	${\ displaystyle A_ {2}}$	${\ displaystyle C_ {2}}$	${\ displaystyle G_ {2}}$
2	A 2	C 2	G 2
3	A 2 + =${\ displaystyle {\ tilde {A}} _ {2}}$	C 2 + =${\ displaystyle {\ tilde {C}} _ ​​{2}}$	G 2 + =${\ displaystyle {\ tilde {G}} _ {2}}$
4	A 2 ++	C 2 ++	G 2 ++
5	A 2 +++	C 2 +++	G 2 +++
Det (M n )	3 (3- n )	2 (3- n )	3- n