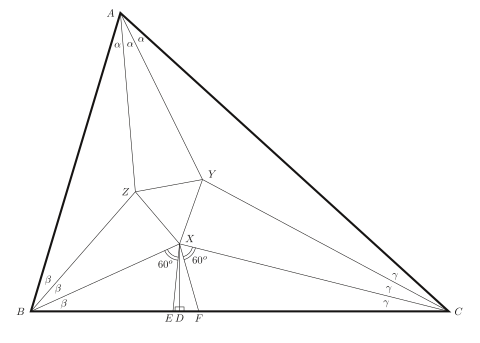
Teorema do trissetor de Morley - Morley's trisector theorem

Se cada ângulo do vértice do triângulo externo for trissecionado, o teorema do trissetor de Morley afirma que o triângulo roxo será equilátero.

Na geometria plana , o teorema do trissetor de Morley afirma que, em qualquer triângulo , os três pontos de intersecção dos trisetores de ângulo adjacentes formam um triângulo equilátero , denominado primeiro triângulo de Morley ou simplesmente triângulo de Morley . O teorema foi descoberto em 1899 pelo matemático anglo-americano Frank Morley . Possui várias generalizações; em particular, se todos os trissetores são interceptados, obtém-se quatro outros triângulos equiláteros.

Provas

Existem muitas provas do teorema de Morley, algumas das quais são muito técnicas. Várias provas iniciais foram baseadas em cálculos trigonométricos delicados . Provas recentes incluem uma prova algébrica de Alain Connes  ( 1998 , 2004 ) estendendo o teorema a campos gerais além da característica três, e a prova de geometria elementar de John Conway . O último começa com um triângulo equilátero e mostra que um triângulo pode ser construído em torno dele, que será semelhante a qualquer triângulo selecionado. O teorema de Morley não se aplica à geometria esférica e hiperbólica .

Fig 1. Prova elementar do teorema do trissetor de Morley

Uma prova usa a identidade trigonométrica

${\ displaystyle \ sin (3 \ theta) = 4 \ sin \ theta \ sin (60 ^ {\ circ} + \ theta) \ sin (120 ^ {\ circ} + \ theta)}$

( 1 )

que, usando a soma da identidade de dois ângulos, pode ser mostrado como sendo igual a

${\ displaystyle \ sin (3 \ theta) = - 4 \ sin ^ {3} \ theta +3 \ sin \ theta.}$

A última equação pode ser verificada aplicando a soma da identidade de dois ângulos ao lado esquerdo duas vezes e eliminando o cosseno.

Os pontos são construídos conforme mostrado. Temos , a soma dos ângulos de qualquer triângulo, portanto , os ângulos do triângulo são e ${\ displaystyle D, E, F}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle 3 \ alpha +3 \ beta +3 \ gamma = 180 ^ {\ circ}}$${\ displaystyle \ alpha + \ beta + \ gamma = 60 ^ {\ circ}.}$${\ displaystyle XEF}$${\ displaystyle \ alpha, (60 ^ {\ circ} + \ beta),}$${\ displaystyle (60 ^ {\ circ} + \ gamma).}$

Da figura

${\ displaystyle \ sin (60 ^ {\ circ} + \ beta) = {\ frac {\ overline {DX}} {\ overline {XE}}}}$

( 2 )

e

${\ displaystyle \ sin (60 ^ {\ circ} + \ gamma) = {\ frac {\ overline {DX}} {\ overline {XF}}}.}$

( 3 )

Também da figura

${\ displaystyle \ angle {AYC} = 180 ^ {\ circ} - \ alpha - \ gamma = 120 ^ {\ circ} + \ beta}$

e

${\ displaystyle \ angle {AZB} = 120 ^ {\ circ} + \ gamma.}$

( 4 )

A lei dos senos aplicada a triângulos e rendimentos ${\ displaystyle AYC}$${\ displaystyle AZB}$

${\ displaystyle \ sin (120 ^ {\ circ} + \ beta) = {\ frac {\ overline {AC}} {\ overline {AY}}} \ sin \ gamma}$

( 5 )

e

${\ displaystyle \ sin (120 ^ {\ circ} + \ gamma) = {\ frac {\ overline {AB}} {\ overline {AZ}}} \ sin \ beta.}$

( 6 )

Expresse a altura do triângulo de duas maneiras ${\ displaystyle ABC}$

${\ displaystyle h = {\ overline {AB}} \ sin (3 \ beta) = {\ overline {AB}} \ cdot 4 \ sin \ beta \ sin (60 ^ {\ circ} + \ beta) \ sin ( 120 ^ {\ circ} + \ beta)}$

e

${\ displaystyle h = {\ overline {AC}} \ sin (3 \ gamma) = {\ overline {AC}} \ cdot 4 \ sin \ gamma \ sin (60 ^ {\ circ} + \ gamma) \ sin ( 120 ^ {\ circ} + \ gamma).}$

onde a equação (1) foi usada para substituir e nessas duas equações. Substituir as equações (2) e (5) na equação e as equações (3) e (6) na equação dá ${\ displaystyle \ sin (3 \ beta)}$${\ displaystyle \ sin (3 \ gamma)}$${\ displaystyle \ beta}$${\ displaystyle \ gamma}$

${\ displaystyle h = 4 {\ overline {AB}} \ sin \ beta \ cdot {\ frac {\ overline {DX}} {\ overline {XE}}} \ cdot {\ frac {\ overline {AC}} { \ overline {AY}}} \ sin \ gamma}$

e

${\ displaystyle h = 4 {\ overline {AC}} \ sin \ gamma \ cdot {\ frac {\ overline {DX}} {\ overline {XF}}} \ cdot {\ frac {\ overline {AB}} { \ overline {AZ}}} \ sin \ beta}$

Uma vez que os numeradores são iguais

${\ displaystyle {\ overline {XE}} \ cdot {\ overline {AY}} = {\ overline {XF}} \ cdot {\ overline {AZ}}}$

ou

${\ displaystyle {\ frac {\ overline {XE}} {\ overline {XF}}} = {\ frac {\ overline {AZ}} {\ overline {AY}}}.}$

Como o ângulo e o ângulo são iguais e os lados que formam esses ângulos têm a mesma proporção, os triângulos e são semelhantes. ${\ displaystyle EXF}$${\ displaystyle ZAY}$${\ displaystyle XEF}$${\ displaystyle AZY}$

Ângulos semelhantes e iguais , e ângulos semelhantes e iguais Argumentos semelhantes produzem os ângulos de base de triângulos e ${\ displaystyle AYZ}$${\ displaystyle XFE}$${\ displaystyle (60 ^ {\ circ} + \ gamma)}$${\ displaystyle AZY}$${\ displaystyle XEF}$${\ displaystyle (60 ^ {\ circ} + \ beta).}$${\ displaystyle BXZ}$${\ displaystyle CYX.}$

Em particular, o ângulo é encontrado e, pela figura, vemos que ${\ displaystyle BZX}$${\ displaystyle (60 ^ {\ circ} + \ alpha)}$

${\ displaystyle \ angle {AZY} + \ angle {AZB} + \ angle {BZX} + \ angle {XZY} = 360 ^ {\ circ}.}$

Substituindo rendimentos

${\ displaystyle (60 ^ {\ circ} + \ beta) + (120 ^ {\ circ} + \ gamma) + (60 ^ {\ circ} + \ alpha) + \ angle {XZY} = 360 ^ {\ circ }}$

onde a equação (4) foi usada para ângulo e, portanto, ${\ displaystyle AZB}$

${\ displaystyle \ angle {XZY} = 60 ^ {\ circ}.}$

Da mesma forma, os outros ângulos do triângulo são encontrados para ser ${\ displaystyle XYZ}$${\ displaystyle 60 ^ {\ circ}.}$

Lado e área

O primeiro triângulo Morley tem comprimentos laterais

${\ displaystyle a ^ {\ prime} = b ^ {\ prime} = c ^ {\ prime} = 8R \ sin (A / 3) \ sin (B / 3) \ sin (C / 3), \,}$

onde R é o circumradius do triângulo original e A, B e C são os ângulos do triângulo original. Uma vez que a área de um triângulo equilátero é a área do triângulo de Morley pode ser expressa como ${\ displaystyle {\ tfrac {\ sqrt {3}} {4}} a '^ {2},}$

${\ displaystyle {\ text {Area}} = 16 {\ sqrt {3}} R ^ {2} \ sin ^ {2} (A / 3) \ sin ^ {2} (B / 3) \ sin ^ { 2} (C / 3).}$

Triângulos de Morley

O teorema de Morley envolve 18 triângulos equiláteros. O triângulo descrito no teorema do trissetor acima, chamado de primeiro triângulo de Morley , tem vértices dados em coordenadas trilineares em relação a um triângulo ABC da seguinte maneira:

A - vértice = 1: 2 cos ( C / 3): 2 cos ( B / 3)

B -vertex = 2 cos ( C / 3): 1: 2 cos ( A / 3)

C- vértice = 2 cos ( B / 3): 2 cos ( A / 3): 1

Outro dos triângulos equiláteros de Morley que também é um triângulo central é chamado de segundo triângulo de Morley e é dado por estes vértices:

A- vértice = 1: 2 cos ( C / 3 - 2π / 3): 2 cos ( B / 3 - 2π / 3)

B- vértice = 2 cos ( C / 3 - 2π / 3): 1: 2 cos ( A / 3 - 2π / 3)

C- vértice = 2 cos ( B / 3 - 2π / 3): 2 cos ( A / 3 - 2π / 3): 1

O terceiro dos 18 triângulos equiláteros de Morley que também é um triângulo central é chamado de terceiro triângulo de Morley e é dado por estes vértices:

A- vértex = 1: 2 cos ( C / 3 - 4π / 3): 2 cos ( B / 3 - 4π / 3)

B -vertex = 2 cos ( C / 3 - 4π / 3): 1: 2 cos ( A / 3 - 4π / 3)

C- vértice = 2 cos ( B / 3 - 4π / 3): 2 cos ( A / 3 - 4π / 3): 1

O primeiro, o segundo e o terceiro triângulos de Morley são homotéticos aos pares . Outra triângulo homotética é formado pelos três pontos X sobre a circunferência circunscrita do triângulo ABC em que a linha XX  ^-1 é tangente ao círculo circunscrito, onde X  ^-1 indica o conjugado isogonal de X . Este triângulo equilátero, denominado triângulo circuntangencial , tem estes vértices:

A- vértice = csc ( C / 3 - B / 3): csc ( B / 3 + 2 C / 3): −csc ( C / 3 + 2 B / 3)

B- vértice = −csc ( A / 3 + 2 C / 3): csc ( A / 3 - C / 3): csc ( C / 3 + 2 A / 3)

C- vértice = csc ( A / 3 + 2 B / 3): −csc ( B / 3 + 2 A / 3): csc ( B / 3 - A / 3)

Um quinto triângulo equilátero, também homotético aos demais, é obtido girando-se o triângulo circuntangencial π / 6 em torno de seu centro. Chamado de triângulo circunormal , seus vértices são os seguintes:

A- vértice = sec ( C / 3 - B / 3): −sec ( B / 3 + 2 C / 3): −sec ( C / 3 + 2 B / 3)

B- vértice = −sec ( A / 3 + 2 C / 3): seg ( A / 3 - C / 3): −sec ( C / 3 + 2 A / 3)

C- vértice = −seg ( A / 3 + 2 B / 3): −seg ( B / 3 + 2 A / 3): sec ( B / 3 - A / 3)

Uma operação chamada "extroversão" pode ser usada para obter um dos 18 triângulos de Morley de outro. Cada triângulo pode ser extrovertido de três maneiras diferentes; os 18 triângulos de Morley e 27 pares extrovertidos de triângulos formam os 18 vértices e 27 arestas do gráfico de Pappus .

Centros de triângulo relacionados

O centróide do primeiro triângulo de Morley é dado em coordenadas trilineares por

Centro de Morley = X (356) = cos ( A / 3) + 2 cos ( B / 3) cos ( C / 3): cos ( B / 3) + 2 cos ( C / 3) cos ( A / 3): cos ( C / 3) + 2 cos ( A / 3) cos ( B / 3).

O primeiro triângulo de Morley é a perspectiva do triângulo ABC : as linhas, cada uma conectando um vértice do triângulo original com o vértice oposto do triângulo de Morley, coincidem no ponto

1º centro Morley – Taylor – Marr = X (357) = seg ( A / 3): seg ( B / 3): seg ( C / 3).

Veja também

• Trissecção angular
• Pontos Hofstadter
• Morley centers

Notas

Referências

• Connes, Alain (1998), "Uma nova prova do teorema de Morley" , Publicações Mathématiques de l'IHÉS , S88 : 43-46 .
• Connes, Alain (dezembro de 2004), "Symmetries" (PDF) , European Mathematical Society Newsletter , 54 .
• Coxeter, HSM ; Greitzer, SL (1967), Geometry Revisited , The Mathematical Association of America , LCCN   67-20607
• Francis, Richard L. (2002), "Modern Mathematical Milestones: Morley's Mystery" (PDF) , Missouri Journal of Mathematical Sciences , 14 (1), doi : 10.35834 / 2002/1401016 .
• Guy, Richard K. (2007), "The lighthouse teorema, Morley & Malfatti — a budget of paradoxes" (PDF) , American Mathematical Monthly , 114 (2): 97–141, doi : 10.1080 / 00029890.2007.11920398 , JSTOR   27642143 , MR   2290364 , arquivado do original (PDF) em 01-04-2010 .
• Oakley, CO; Baker, JC (1978), "The Morley trisector teorema", American Mathematical Monthly , 85 (9): 737-745, doi : 10.2307 / 2321680 , JSTOR   2321680 .
• Taylor, F. Glanville; Marr, WL (1913–14), "Os seis trisectores de cada um dos ângulos de um triângulo", Proceedings of the Edinburgh Mathematical Society , 33 : 119–131, doi : 10.1017 / S0013091500035100 .

links externos

• Teorema de Morleys em MathWorld
• Teorema da trissecção de Morley em MathPages
• Teorema de Morley de Oleksandr Pavlyk, The Wolfram Demonstrations Project .