Característica de Euler - Euler characteristic
Em matemática , e mais especificamente na topologia algébrica e combinatória poliédrica , a característica de Euler (ou número de Euler , ou característica de Euler-Poincaré ) é um invariante topológico , um número que descreve a forma ou estrutura de um espaço topológico , independentemente de como ele seja dobrado. É comumente denotado por ( chi da letra grega minúscula ).
A característica de Euler foi originalmente definida para poliedros e usada para provar vários teoremas sobre eles, incluindo a classificação dos sólidos platônicos . Foi declarado para sólidos platônicos em 1537 em um manuscrito não publicado por Francesco Maurolico . Leonhard Euler , que deu o nome ao conceito, apresentou-o para poliedros convexos de maneira mais geral, mas não conseguiu provar rigorosamente que é um invariante. Na matemática moderna, a característica de Euler surge da homologia e, de forma mais abstrata, da álgebra homológica .
Poliedro
A característica de Euler foi definida classicamente para as superfícies dos poliedros, de acordo com a fórmula
onde V , E e F são respectivamente os números de vértices (cantos), arestas e faces no poliedro fornecido. Qualquer superfície de poliedro convexo tem a característica de Euler
Essa equação, declarada por Leonhard Euler em 1758, é conhecida como fórmula do poliedro de Euler . Corresponde à característica de Euler da esfera (ou seja, χ = 2) e se aplica de forma idêntica aos poliedros esféricos . Uma ilustração da fórmula em todos os poliedros platônicos é fornecida abaixo.
| Nome | Imagem | Vértices V |
Edges E |
Faces F |
Característica de Euler: V - E + F |
|---|---|---|---|---|---|
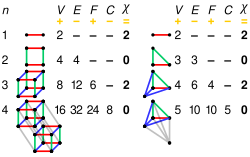
| Tetraedro |

|
4 | 6 | 4 | 2 |
| Hexaedro ou cubo |

|
8 | 12 | 6 | 2 |
| Octaedro |

|
6 | 12 | 8 | 2 |
| Dodecaedro |
|
20 | 30 | 12 | 2 |
| Icosaedro |

|
12 | 30 | 20 | 2 |
As superfícies de poliedros não convexos podem ter várias características de Euler:
| Nome | Imagem | Vértices V |
Edges E |
Faces F |
Característica de Euler: V - E + F |
|---|---|---|---|---|---|
| Tetrahemihexahedron |

|
6 | 12 | 7 | 1 |
| Octaemioctaedro |

|
12 | 24 | 12 | 0 |
| Cubohemioctaedro |

|
12 | 24 | 10 | -2 |
| Dodecaedro estrelado pequeno |

|
12 | 30 | 12 | -6 |
| Grande dodecaedro estrelado |

|
20 | 30 | 12 | 2 |
Para poliedros regulares, Arthur Cayley derivou uma forma modificada da fórmula de Euler usando a densidade D , densidade de figura de vértice d v e densidade de face :
Esta versão vale tanto para poliedros convexos (onde as densidades são todas 1) quanto para poliedros não convexos de Kepler-Poinsot .
Todos os poliedros projetivos têm a característica de Euler 1, como o plano projetivo real , enquanto as superfícies dos poliedros toroidais têm a característica de Euler 0, como o toro .
Gráficos planos
A característica de Euler pode ser definida para gráficos planos conectados pela mesma fórmula que para superfícies poliédricas, onde F é o número de faces no gráfico, incluindo a face externa.
A característica de Euler de qualquer grafo plano conectado G é 2. Isso é facilmente provado por indução no número de faces determinado por G, começando com uma árvore como o caso base. Para árvores e . Se G tem componentes C (gráficos desconectados), o mesmo argumento por indução em F mostra isso . Um dos poucos artigos de teoria dos grafos de Cauchy também prova esse resultado.
Via projeção estereográfica, o plano mapeia para a 2-esfera, de modo que um gráfico conectado mapeia para uma decomposição poligonal da esfera, que tem a característica de Euler 2. Este ponto de vista está implícito na prova de Cauchy da fórmula de Euler dada abaixo.
Prova da fórmula de Euler
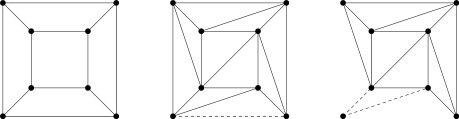
Existem muitas provas da fórmula de Euler. Um foi dado por Cauchy em 1811, como segue. Ele se aplica a qualquer poliedro convexo e, mais geralmente, a qualquer poliedro cujo limite seja topologicamente equivalente a uma esfera e cujas faces sejam topologicamente equivalentes a discos.
Remova uma face da superfície poliédrica. Ao afastar as arestas da face faltante uma da outra, deformar todo o resto em um gráfico plano de pontos e curvas, de forma que o perímetro da face faltante seja colocado externamente, circundando o gráfico obtido, conforme ilustrado pelo primeiro dos três gráficos para o caso especial do cubo. (A suposição de que a superfície poliédrica é homeomórfica à esfera no início é o que torna isso possível.) Após essa deformação, as faces regulares geralmente não são mais regulares. O número de vértices e arestas permaneceu o mesmo, mas o número de faces foi reduzido em 1. Portanto, provar a fórmula de Euler para o poliedro se reduz a provar V - E + F = 1 para este objeto plano deformado.
Se houver uma face com mais de três lados, desenhe uma diagonal - ou seja, uma curva através da face conectando dois vértices que ainda não estão conectados. Isto adiciona uma aresta e uma face e não altera o número de vértices, de modo que não altera a quantidade V - E + F . (A suposição de que todas as faces são discos é necessária aqui, para mostrar, por meio do teorema da curva de Jordan, que essa operação aumenta o número de faces em um.) Continue adicionando arestas dessa maneira até que todas as faces sejam triangulares.
Aplique repetidamente uma das duas transformações a seguir, mantendo a invariante de que o limite externo é sempre um ciclo simples :
- Remova um triângulo com apenas uma aresta adjacente ao exterior, conforme ilustrado pelo segundo gráfico. Isto diminui o número de arestas e faces por um cada e não altera o número de vértices, de modo que preserva V - E + F .
- Remova um triângulo com duas arestas compartilhadas pelo exterior da rede, conforme ilustrado pelo terceiro gráfico. Cada triângulo remoção remove um vértice, dois bordos e uma face, de modo que preserva V - E + F .
Essas transformações eventualmente reduzem o gráfico planar a um único triângulo. (Sem o invariante de ciclo simples, a remoção de um triângulo pode desconectar os triângulos restantes, invalidando o resto do argumento. Uma ordem de remoção válida é um exemplo elementar de um casco .)
Neste ponto, o triângulo solitário tem V = 3, E = 3 e F = 1, de modo que V - E + F = 1. Como cada uma das duas etapas de transformação acima preservou essa quantidade, mostramos V - E + F = 1 para o objeto plano deformado, demonstrando assim V - E + F = 2 para o poliedro. Isso prova o teorema.
Para provas adicionais, veja Vinte Provas da Fórmula de Euler, de David Eppstein . Múltiplas provas, incluindo suas falhas e limitações, são usadas como exemplos em Provas e Refutações de Imre Lakatos .
Definição topológica
As superfícies poliédricas discutidas acima são, na linguagem moderna, complexos CW finitos bidimensionais . (Quando apenas faces triangulares são usadas, elas são complexos simpliciais finitos bidimensionais .) Em geral, para qualquer complexo CW finito, a característica de Euler pode ser definida como a soma alternada
onde k n denota o número de células de dimensão n no complexo.
Da mesma forma, para um complexo simplicial , a característica de Euler é igual à soma alternada
onde k n denota o número de n -simplexes no complexo.
Alternativa de número Betti
Mais ainda, geralmente, para qualquer espaço topológico , podemos definir o n th número Betti b n como o posto de o n -simo homologia singular grupo. A característica de Euler pode então ser definida como a soma alternada
Essa quantidade é bem definida se os números de Betti forem todos finitos e se eles forem zero além de um determinado índice n 0 . Para complexos simpliciais, esta não é a mesma definição do parágrafo anterior, mas um cálculo de homologia mostra que as duas definições fornecerão o mesmo valor para .
Propriedades
A característica de Euler se comporta bem com respeito a muitas operações básicas em espaços topológicos, como segue.
Invariância de homotopia
A homologia é um invariante topológico e, além disso, um invariante de homotopia : dois espaços topológicos que são equivalentes de homotopia têm grupos de homologia isomórficos . Conclui-se que a característica de Euler também é uma invariante homotópica.
Por exemplo, qualquer espaço contrátil (ou seja, uma homotopia equivalente a um ponto) tem homologia trivial, o que significa que o 0º número de Betti é 1 e os outros 0. Portanto, sua característica de Euler é 1. Este caso inclui o espaço euclidiano de qualquer dimensão , bem como a bola de unidade sólida em qualquer espaço euclidiano - o intervalo unidimensional, o disco bidimensional, a bola tridimensional, etc.
Para outro exemplo, qualquer poliedro convexo é homeomórfico à bola tridimensional , portanto, sua superfície é homeomórfica (portanto, homotopia equivalente) à esfera bidimensional , que tem a característica de Euler 2. Isso explica por que os poliedros convexos têm a característica de Euler 2.
Princípio de inclusão-exclusão
Se M e N são quaisquer dois espaços topológicos, então a característica de Euler de sua união disjunta é a soma de suas características de Euler, uma vez que a homologia é aditiva sob união disjunta:
De maneira mais geral, se M e N são subespaços de um espaço X maior , então também são sua união e interseção. Em alguns casos, a característica de Euler obedece a uma versão do princípio de inclusão-exclusão :
Isso é verdade nos seguintes casos:
- se M e N são um casal excisivo . Em particular, se os interiores de M e N dentro da união ainda cobrem a união.
- se X é um espaço localmente compacto e se usa características de Euler com suportes compactos , nenhuma suposição sobre M ou N é necessária.
- se X for um espaço estratificado cujos estratos são pares dimensionais, o princípio de inclusão-exclusão é válido se M e N forem uniões de estratos. Isso se aplica em particular se M e N são subvariedades de uma variedade algébrica complexa .
Em geral, o princípio de inclusão-exclusão é falso. Um contra-exemplo é dado pela tendo X para ser a verdadeira linha , M um subconjunto constituído por um ponto e N o complemento de M .
Soma conectada
Para dois manifolds n fechados conectados, pode-se obter um novo manifold conectado por meio da operação de soma conectada . A característica de Euler está relacionada pela fórmula
Propriedade do produto
Além disso, a característica de Euler de qualquer espaço de produto M × N é
Essas propriedades de adição e multiplicação também são apreciadas pela cardinalidade de conjuntos . Dessa forma, a característica de Euler pode ser vista como uma generalização da cardinalidade; veja [1] .
Espaços de cobertura
Da mesma forma, para um espaço de cobertura de folha k , um tem
De modo mais geral, para um espaço de cobertura ramificado , a característica de Euler da cobertura pode ser calculada a partir do acima, com um fator de correção para os pontos de ramificação, o que produz a fórmula de Riemann-Hurwitz .
Propriedade de fibração
A propriedade do produto é muito mais geral, para fibrações com certas condições.
Se for uma fibração com fibra F, com a base B conectada ao caminho , e a fibração for orientável sobre um campo K, então a característica de Euler com coeficientes no campo K satisfaz a propriedade do produto:
Isso inclui espaços de produto e espaços de cobertura como casos especiais e pode ser comprovado pela sequência espectral de Serre na homologia de uma fibração.
Para feixes de fibras, isso também pode ser entendido em termos de um mapa de transferência - note que isso é um levantamento e vai "para o lado errado" - cuja composição com o mapa de projeção é a multiplicação pela classe de Euler da fibra:
Exemplos
Superfícies
A característica de Euler pode ser calculada facilmente para superfícies gerais, encontrando uma poligonização da superfície (ou seja, uma descrição como um complexo CW ) e usando as definições acima.
| Nome | Imagem | χ |
|---|---|---|
| Intervalo |

|
1 |
| Círculo |

|
0 |
| Disco |

|
1 |
| Esfera |

|
2 |
|
Toro (produto de dois círculos) |

|
0 |
| Toro duplo |

|
-2 |
| Toro triplo |

|
-4 |
|
Plano projetivo real |

|
1 |
| Tira de Möbius |
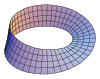
|
0 |
| Garrafa de Klein |
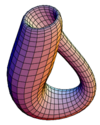
|
0 |
| Duas esferas (não conectadas) (união disjunta de duas esferas) |

|
2 + 2 = 4 |
| Três esferas (não conectadas) (união disjunta de três esferas) |
  
|
2 + 2 + 2 = 6 |
|
esferas (não conectadas) (união disjunta de n esferas) |
 . . . . . .
|
2 + ... + 2 = 2n |
Bola de futebol
É comum construir bolas de futebol costurando peças pentagonais e hexagonais, com três peças encontrando-se em cada vértice (ver por exemplo o Adidas Telstar ). Se pentágonos P e hexágonos H são usados, então existem faces F = P + H , V = (5 P + 6 H ) / 3 vértices e E = (5 P + 6 H ) / 2 arestas. A característica de Euler é, portanto,
Como a esfera tem a característica de Euler 2, segue-se que P = 12. Ou seja, uma bola de futebol construída dessa forma sempre tem 12 pentágonos. Em princípio, o número de hexágonos é ilimitado. Este resultado é aplicável a fulerenos e poliedros Goldberg .
Dimensões arbitrárias
4 politopo regular |
V ( k 0 ) |
E ( k 1 ) |
F ( k 2 ) |
C ( k 3 ) |
= V - E + F - C |
|---|---|---|---|---|---|
| 5 células | 5 | 10 | 10 | 5 | 0 |
| 8 células | 16 | 32 | 24 | 8 | 0 |
| 16 células | 8 | 24 | 32 | 16 | 0 |
| 24 células | 24 | 96 | 96 | 24 | 0 |
| 120 células | 600 | 1200 | 720 | 120 | 0 |
| 600 células | 120 | 720 | 1200 | 600 | 0 |
A esfera n- dimensional tem grupos de homologia singulares iguais a
portanto, tem o número de Betti 1 nas dimensões 0 e n , e todos os outros números de Betti são 0. Sua característica de Euler é então 1 + (−1) n - ou seja, 0 ou 2.
O espaço projetivo real n- dimensional é o quociente da esfera n pelo mapa antípoda . Conclui-se que sua característica de Euler é exatamente a metade da esfera correspondente - 0 ou 1.
O toro n- dimensional é o espaço do produto de n círculos. Sua característica de Euler é 0, pela propriedade do produto. Mais geralmente, qualquer variedade compacta paralelizável , incluindo qualquer grupo de Lie compacto , tem a característica de Euler 0.
A característica de Euler de qualquer variedade fechada de dimensão ímpar também é 0. O caso dos exemplos orientáveis é um corolário da dualidade de Poincaré . Esta propriedade se aplica mais geralmente a qualquer espaço estratificado compacto cujos estratos tenham dimensão ímpar. Também se aplica a coletores não orientáveis de dimensão ímpar fechados, por meio da tampa dupla orientável bi-para-um .
Relações com outros invariantes
A característica de Euler de uma superfície orientável fechada pode ser calculada a partir de seu gênero g (o número de toros em uma decomposição de soma conectada da superfície; intuitivamente, o número de "alças") como
A característica de Euler de uma superfície fechada não orientável pode ser calculada a partir de seu gênero k não orientável (o número de planos projetivos reais em uma decomposição de soma conectada da superfície) como
Para variedades lisas fechadas, a característica de Euler coincide com o número de Euler , ou seja, a classe de Euler de seu feixe tangente avaliado na classe fundamental de uma variedade. A classe de Euler, por sua vez, se relaciona a todas as outras classes características de feixes de vetores .
Para variedades Riemannianas fechadas , a característica de Euler também pode ser encontrada integrando a curvatura; veja o teorema de Gauss-Bonnet para o caso bidimensional e o teorema de Gauss-Bonnet generalizado para o caso geral.
Um análogo discreto do teorema de Gauss-Bonnet é o teorema de Descartes de que o "defeito total" de um poliedro , medido em círculos completos, é a característica de Euler do poliedro; veja defeito (geometria) .
O teorema de Hadwiger caracteriza a característica de Euler como a função de conjunto única ( até a multiplicação escalar ) invariante à translação, finitamente aditiva, não necessariamente não negativa definida em uniões finitas de conjuntos convexos compactos em R n que é "homogênea de grau 0".
Generalizações
Para cada complexo de células combinatórias , define-se a característica de Euler como o número de células 0, menos o número de células 1, mais o número de células 2, etc., se essa soma alternada for finita. Em particular, a característica de Euler de um conjunto finito é simplesmente sua cardinalidade, e a característica de Euler de um gráfico é o número de vértices menos o número de arestas.
De forma mais geral, pode-se definir a característica de Euler de qualquer complexo de cadeia como a soma alternada das classificações dos grupos de homologia do complexo de cadeia, assumindo que todas essas classificações são finitas.
Uma versão da característica de Euler usada na geometria algébrica é a seguinte. Para qualquer feixe coerente em um esquema X adequado , define-se sua característica de Euler como
onde está a dimensão do i- ésimo grupo de cohomologia de feixes de . Nesse caso, as dimensões são todas finitas pelo teorema da finitude de Grothendieck . Este é um exemplo da característica de Euler de um complexo de cadeia, onde o complexo de cadeia é uma resolução finita de feixes acíclicos.
Outra generalização do conceito de característica de Euler em variedades vem de orbifolds (veja a característica de Euler de um orbifold ). Embora cada variedade tenha uma característica de Euler inteira, um orbifold pode ter uma característica de Euler fracionária. Por exemplo, o orbifold em forma de lágrima tem a característica de Euler 1 + 1 / p , onde p é um número primo correspondente ao ângulo do cone 2 π / p .
O conceito de Euler característico da homologia reduzida de um poset finito limitado é outra generalização, importante em combinatória . Um poset é "limitado" se tiver elementos menores e maiores; chame-os de 0 e 1. A característica de Euler de tal poset é definida como o inteiro μ (0,1), onde μ é a função de Möbius na álgebra de incidência daquele poset .
Isso pode ser generalizado definindo uma característica de Euler avaliada em Q para certas categorias finitas , uma noção compatível com as características de Euler de gráficos, orbifolds e posets mencionados acima. Nesse cenário, a característica de Euler de um grupo finito ou monóide G é 1 / | G |, e a característica de Euler de um grupóide finito é a soma de 1 / | G i |, onde escolhemos um grupo representativo G i para cada componente conectado do grupóide.
Veja também
- Cálculo de Euler
- Aula de Euler
- Lista de tópicos com o nome de Leonhard Euler
- Lista de poliedros uniformes
Referências
Notas
Bibliografia
- Richeson, David S .; Gema de Euler: a fórmula do poliedro e o nascimento da topologia . Princeton University Press 2008.
Leitura adicional
- Flegg, H. Graham; From Geometry to Topology , Dover 2001, p. 40