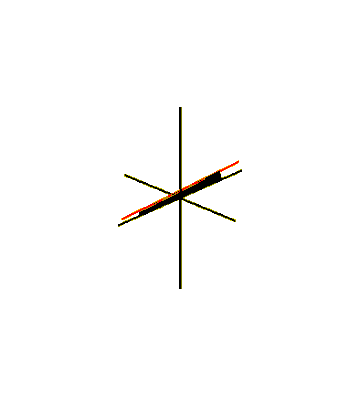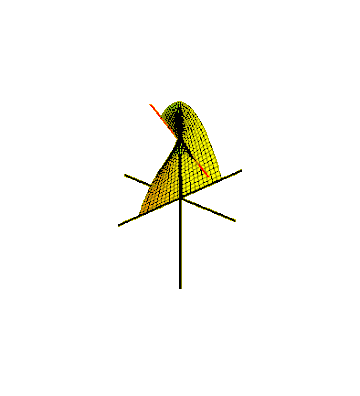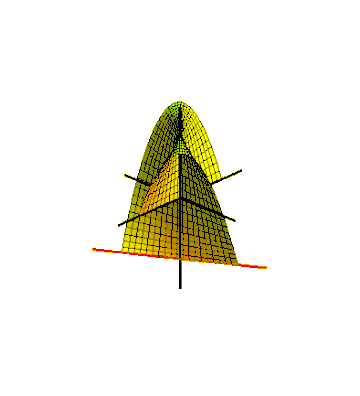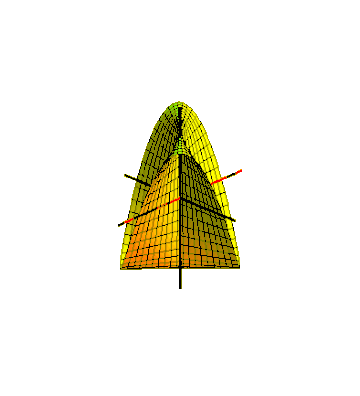tira de Möbius -Möbius strip

Uma tira de Möbius feita com papel e fita adesiva

Em matemática , uma tira de Möbius, banda de Möbius ou laço de Möbius é uma superfície que pode ser formada unindo as extremidades de uma tira de papel com uma meia torção. Como objeto matemático, foi descoberto por Johann Benedict Listing e August Ferdinand Möbius em 1858, mas já havia aparecido em mosaicos romanos do século III dC. A faixa de Möbius é uma superfície não orientável , o que significa que dentro dela não se pode distinguir consistentemente as voltas no sentido horário das no sentido anti-horário. Toda superfície não orientável contém uma faixa de Möbius.

Como um espaço topológico abstrato , a faixa de Möbius pode ser incorporada no espaço euclidiano tridimensional de muitas maneiras diferentes: uma meia torção no sentido horário é diferente de uma meia torção no sentido anti-horário e também pode ser incorporada com números ímpares de torções maiores que um, ou com uma linha central com nós . Quaisquer dois encaixes com o mesmo nó para a linha central e o mesmo número e direção de torções são topologicamente equivalentes . Todos esses encaixes têm apenas um lado, mas quando encaixados em outros espaços, a faixa de Möbius pode ter dois lados. Tem apenas uma única curva limite .

Várias construções geométricas da faixa de Möbius fornecem estrutura adicional. Ele pode ser varrido como uma superfície pautada por um segmento de linha girando em um plano rotativo, com ou sem auto-cruzamentos. Uma tira de papel fina com suas extremidades unidas para formar uma tira de Möbius pode dobrar suavemente como uma superfície desenvolvível ou ser dobrada plana ; as tiras de Möbius achatadas incluem o trihexaflexagon . A faixa de Möbius sudanesa é uma superfície mínima em uma hiperesfera , e a faixa de Meeks Möbius é uma superfície mínima de auto-interseção no espaço euclidiano comum. Tanto a faixa de Möbius sudanesa quanto outra faixa de Mobius que se autointersecciona, a cross-cap, têm um limite circular. Uma faixa de Möbius sem seu limite, chamada de faixa de Möbius aberta, pode formar superfícies de curvatura constante . Certos espaços altamente simétricos cujos pontos representam linhas no plano têm a forma de uma faixa de Möbius.

As muitas aplicações das tiras Möbius incluem cintos mecânicos que se desgastam uniformemente em ambos os lados, montanhas-russas de duas pistas cujos carros alternam entre as duas pistas e mapas do mundo impressos para que os antípodas apareçam um em frente ao outro. As tiras de Möbius aparecem em moléculas e dispositivos com novas propriedades elétricas e eletromecânicas, e têm sido usadas para provar resultados de impossibilidade na teoria da escolha social . Na cultura popular, as tiras de Möbius aparecem em obras de MC Escher , Max Bill e outros, e no desenho do símbolo de reciclagem . Muitos conceitos arquitetônicos foram inspirados pela faixa de Möbius, incluindo o projeto de construção do Hall da Fama da NASCAR . Artistas como Harry Blackstone Sr. e Thomas Nelson Downs basearam truques de mágica de palco nas propriedades da tira de Möbius. Os cânones de JS Bach foram analisados ​​usando tiras de Möbius. Muitas obras de ficção especulativa apresentam tiras de Möbius; mais geralmente, uma estrutura de enredo baseada na tira de Möbius, de eventos que se repetem com uma reviravolta, é comum na ficção.

História

Mosaico do antigo Sentinum representando Aion segurando uma tira de Möbius

Bomba de corrente com uma corrente de transmissão Möbius, por Ismail al-Jazari (1206)

A descoberta da tira de Möbius como objeto matemático é atribuída independentemente aos matemáticos alemães Johann Benedict Listing e August Ferdinand Möbius em 1858. No entanto, já era conhecida muito antes, tanto como objeto físico quanto em representações artísticas; em particular, pode ser visto em vários mosaicos romanos do século III dC. Em muitos casos, estes meramente descrevem fitas enroladas como limites. Quando o número de bobinas é ímpar, essas fitas são tiras de Möbius, mas para um número par de bobinas são topologicamente equivalentes a anéis não torcidos . Portanto, se a fita é uma tira de Möbius pode ser uma coincidência, e não uma escolha deliberada. Em pelo menos um caso, uma fita com cores diferentes em lados diferentes foi desenhada com um número ímpar de bobinas, forçando seu artista a fazer um reparo desajeitado no ponto em que as cores não combinavam. Outro mosaico da cidade de Sentinum (representado) mostra o zodíaco , mantido pelo deus Aion , como uma banda com apenas uma torção. Não há evidência clara de que a unilateralidade dessa representação visual do tempo celestial tenha sido intencional; poderia ter sido escolhido apenas como forma de fazer com que todos os signos do zodíaco apareçam no lado visível da tira. Algumas outras representações antigas dos ourobouros ou de decorações em forma de oito também são alegadas para retratar tiras de Möbius, mas se eles pretendiam retratar tiras planas de qualquer tipo não está claro.

Independentemente da tradição matemática, os maquinistas sabem há muito tempo que as correias mecânicas se desgastam com metade da rapidez quando formam tiras de Möbius, porque usam toda a superfície da correia em vez de apenas a superfície interna de uma correia sem torção. Além disso, tal cinto pode ser menos propenso a enrolar de um lado para o outro. Uma descrição escrita inicial desta técnica data de 1871, após as primeiras publicações matemáticas sobre a tira de Möbius. Muito antes, uma imagem de uma bomba de corrente em uma obra de Ismail al-Jazari de 1206 mostra uma configuração de tira de Möbius para sua corrente de transmissão. Outro uso desta superfície foi feito por costureiras em Paris (em data não especificada): eles iniciaram noviços exigindo que eles costurassem uma tira de Möbius como gola em uma peça de roupa.

Propriedades

Um objeto 2D percorrendo uma vez ao redor da faixa de Möbius retorna em forma espelhada

A faixa de Möbius tem várias propriedades curiosas. É uma superfície não orientável : se um objeto bidimensional assimétrico desliza uma vez ao redor da faixa, ele retorna à sua posição inicial como sua imagem espelhada. Em particular, uma seta curva apontando no sentido horário (↻) retornaria como uma seta apontando no sentido anti-horário (↺), implicando que, dentro da faixa de Möbius, é impossível definir consistentemente o que significa estar no sentido horário ou anti-horário. É a superfície não orientável mais simples: qualquer outra superfície é não orientável se e somente se tiver uma faixa de Möbius como subconjunto. Da mesma forma, quando embutida no espaço euclidiano , a faixa de Möbius tem apenas um lado. Um objeto tridimensional que desliza uma vez ao redor da superfície da tira não é espelhado, mas retorna ao mesmo ponto da tira no que parece localmente ser seu outro lado, mostrando que ambas as posições são realmente parte de um único lado . Esse comportamento é diferente de superfícies orientáveis ​​familiares em três dimensões, como aquelas modeladas por folhas planas de papel, canudos cilíndricos ou bolas ocas, para as quais um lado da superfície não está conectado ao outro. No entanto, esta é uma propriedade de sua inserção no espaço e não uma propriedade intrínseca da própria faixa de Möbius: existem outros espaços topológicos nos quais a faixa de Möbius pode ser embutida de modo que tenha dois lados. Por exemplo, se as faces frontal e traseira de um cubo são coladas uma à outra com uma reflexão especular esquerda-direita, o resultado é um espaço topológico tridimensional (o produto cartesiano de uma faixa de Möbius com um intervalo) no qual o topo e as metades inferiores do cubo podem ser separadas uma da outra por uma tira de Möbius de dois lados. Em contraste com discos, esferas e cilindros, para os quais é possível incorporar simultaneamente um conjunto incontável de cópias disjuntas no espaço tridimensional, apenas um número contável de tiras de Möbius pode ser incorporado simultaneamente.

Um caminho ao longo da borda de uma faixa de Möbius, traçado até retornar ao seu ponto inicial na borda, inclui todos os pontos de fronteira da faixa de Möbius em uma única curva contínua. Para uma tira de Möbius formada pela colagem e torção de um retângulo, ela tem o dobro do comprimento da linha central da tira. Nesse sentido, a faixa de Möbius é diferente de um anel sem torção e como um disco circular por ter apenas uma fronteira. Uma faixa de Möbius no espaço euclidiano não pode ser movida ou esticada em sua imagem especular; é um objeto quiral com destro ou canhoto. As tiras de Möbius com números ímpares de meias-torções maiores que um, ou que são atadas antes da colagem, são distintas como subconjuntos embutidos do espaço tridimensional, embora sejam todas equivalentes como superfícies topológicas bidimensionais . Mais precisamente, duas tiras de Möbius são incorporadas de forma equivalente no espaço tridimensional quando suas linhas centrais determinam o mesmo nó e elas têm o mesmo número de torções uma da outra. Com um número par de torções, porém, obtém-se uma superfície topológica diferente, chamada de anel .

A faixa de Möbius pode ser continuamente transformada em sua linha central, tornando-a mais estreita e fixando os pontos na linha central. Essa transformação é um exemplo de retração de deformação , e sua existência significa que a faixa de Möbius tem muitas das mesmas propriedades que sua linha central, que é topologicamente um círculo. Em particular, seu grupo fundamental é o mesmo que o grupo fundamental de um círculo, um grupo cíclico infinito . Portanto, caminhos na faixa de Möbius que começam e terminam no mesmo ponto podem ser distinguidos topologicamente (até homotopia ) apenas pelo número de vezes que eles dão voltas ao redor da faixa.

Cortar a linha central produz uma tira de dois lados (não Möbius)

Um único corte descentralizado separa uma tira de Möbius (roxa) de uma tira de dois lados

Cortar uma tira de Möbius ao longo da linha central com uma tesoura produz uma tira longa com duas meias voltas, em vez de duas tiras separadas. O resultado não é uma tira de Möbius, mas sim topologicamente equivalente a um cilindro. Cortar esta tira duplamente torcida novamente ao longo de sua linha central produz duas tiras duplamente torcidas ligadas. Se, em vez disso, uma tira de Möbius for cortada longitudinalmente, um terço da sua largura, ela produz duas tiras ligadas. Uma das duas é uma tira de Möbius central, mais fina, enquanto a outra tem duas meias torções. Essas formas interligadas, formadas por fatias longitudinais de tiras de Möbius com larguras variadas, às vezes são chamadas de anéis paradrômicos .

Subdivisão em seis regiões mutuamente adjacentes, delimitadas pelo gráfico de Tietze

Solução para o problema das três utilidades em uma faixa de Möbius

A faixa de Möbius pode ser cortada em seis regiões mutuamente adjacentes, mostrando que os mapas na superfície da faixa de Möbius podem às vezes exigir seis cores, em contraste com o teorema de quatro cores para o plano. Seis cores são sempre suficientes. Este resultado faz parte do teorema de Ringel-Youngs , que afirma quantas cores cada superfície topológica precisa. As arestas e vértices dessas seis regiões formam o grafo de Tietze , que é um grafo duplo nesta superfície para o grafo completo de seis vértices, mas não pode ser desenhado sem cruzamentos em um plano . Outra família de grafos que podem ser embutidos na faixa de Möbius, mas não no plano, são as escadas de Möbius , os limites das subdivisões da faixa de Möbius em retângulos que se encontram de ponta a ponta. Estes incluem o gráfico de utilidade, um grafo bipartido completo de seis vértices cuja incorporação na faixa de Möbius mostra que, ao contrário do plano, o problema das três utilidades pode ser resolvido em uma faixa de Möbius transparente. A característica de Euler da faixa de Möbius é zero , o que significa que para qualquer subdivisão da faixa por vértices e arestas em regiões, os números , , e de vértices, arestas e regiões satisfazem . Por exemplo, o grafo de Tietze tem vértices, arestas e regiões; .${\estilo de exibição V}$${\displaystyle E}$${\estilo de exibição F}$${\estilo de exibição V-E+F=0}$${\estilo de exibição 12}$${\estilo de exibição 18}$${\estilo de exibição 6}$${\estilo de exibição 12-18+6=0}$

Construções

Existem muitas maneiras diferentes de definir superfícies geométricas com a topologia da faixa de Möbius, produzindo realizações com propriedades geométricas adicionais.

Varrendo um segmento de linha

Uma faixa de Möbius varrida por um segmento de linha rotativo em um plano rotativo

Conóide de Plücker varrido por um movimento diferente de um segmento de linha

Uma maneira de incorporar a faixa de Möbius no espaço euclidiano tridimensional é varrê-la por um segmento de linha girando em um plano, que por sua vez gira em torno de uma de suas linhas. Para que a superfície varrida se encontre após uma meia torção, o segmento de linha deve girar em torno de seu centro na metade da velocidade angular da rotação do plano. Isso pode ser descrito como uma superfície paramétrica definida por equações para as coordenadas cartesianas de seus pontos,

$${\displaystyle {\begin{aligned}x(u,v)&=\left(1+{\frac {v}{2}}\cos {\frac {u}{2}}\right)\cos u \\y(u,v)&=\left(1+{\frac {v}{2}}\cos {\frac {u}{2}}\right)\sin u\\z(u,v )&={\frac {v}{2}}\sin {\frac {u}{2}}\\\end{alinhado}}}$$

${\displaystyle 0\leq u<2\pi }$

${\displaystyle -1\leq v\leq 1}$

${\displaystyle u}$

${\estilo de exibição v}$

${\ estilo de exibição xy}$

${\estilo de exibição (0,0,0)}$

Uma linha ou segmento de linha varrido em um movimento diferente, girando em um plano horizontal em torno da origem à medida que se move para cima e para baixo, forma o conóide ou cilindroide de Plücker , uma superfície regrada algébrica na forma de uma faixa de Möbius que se cruza. Tem aplicações no projeto de engrenagens .

Superfícies poliédricas e dobras planas

Trihexaflexagon sendo flexionado

Uma tira de papel pode formar uma tira de Möbius achatada no plano dobrando-a em ângulos de modo que sua linha central fique ao longo de um triângulo equilátero e prendendo as extremidades. A faixa mais curta para a qual isso é possível consiste em três triângulos equiláteros, dobrados nas bordas onde dois triângulos se encontram. Sua proporção  – a proporção entre o comprimento da tira e sua largura – é , e o mesmo método de dobra funciona para qualquer proporção maior. Para uma faixa de nove triângulos equiláteros, o resultado é um trihexaflexágono , que pode ser flexionado para revelar diferentes partes de sua superfície. Para tiras muito curtas para aplicar este método diretamente, pode-se primeiro "dobrar em sanfona" a tira em sua direção larga para frente e para trás usando um número par de dobras. Com duas dobras, por exemplo, uma tira se tornaria uma tira dobrada cuja seção transversal tem a forma de um 'N' e permaneceria um 'N' após uma meia torção. A tira dobrada em acordeão mais estreita pode então ser dobrada e unida da mesma forma que uma tira mais longa .${\displaystyle 60^{\circ }}$${\displaystyle {\sqrt {3}}\approx 1,73}$${\estilo de exibição 1\vezes 1}$${\displaystyle 1\times {\tfrac {1}{3}}}$

Tiras de Möbius poliédricas de cinco vértices e dobradas planas

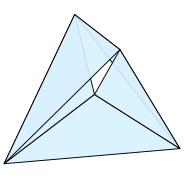
A faixa de Möbius também pode ser embutida como uma superfície poliédrica no espaço ou dobrada no plano, com apenas cinco faces triangulares compartilhando cinco vértices. Nesse sentido, é mais simples que o cilindro , que requer seis triângulos e seis vértices, mesmo quando representado de forma mais abstrata como um complexo simplicial . Uma faixa de Möbius de cinco triângulos pode ser representada mais simetricamente por cinco dos dez triângulos equiláteros de um simplex regular quadridimensional . Essa faixa de Möbius poliédrica de quatro dimensões é a única faixa de Möbius compacta, totalmente quadridimensional e para a qual todos os cortes por hiperplanos a separam em duas partes topologicamente equivalentes a discos ou círculos.

Outros encaixes poliédricos de tiras de Möbius incluem um com quatro quadriláteros convexos como faces, outro com três faces quadrilaterais não convexas e um usando os vértices e o ponto central de um octaedro regular, com um limite triangular . Cada triangulação abstrata do plano projetivo pode ser incorporada em 3D como uma faixa de Möbius poliédrica com um limite triangular após a remoção de uma de suas faces; um exemplo é o plano projetivo de seis vértices obtido pela adição de um vértice à faixa de Möbius de cinco vértices, conectada por triângulos a cada uma de suas arestas limítrofes. No entanto, nem toda triangulação abstrata da faixa de Möbius pode ser representada geometricamente, como uma superfície poliédrica. Para ser realizável, é necessário e suficiente que não haja dois 3 ciclos disjuntos não contráteis na triangulação.

Retângulos suavemente incorporados

Uma tira de Möbius retangular, feita anexando as extremidades de um retângulo de papel, pode ser encaixada suavemente no espaço tridimensional sempre que sua proporção for maior que , a mesma proporção que para a versão de triângulo equilátero dobrado da tira de Möbius. Este encaixe triangular plano pode elevar-se a um encaixe suave em três dimensões, no qual a tira fica plana em três planos paralelos entre três rolos cilíndricos, cada um tangente a dois dos planos. Matematicamente, uma folha de papel suavemente encaixada pode ser modelada como uma superfície desenvolvível , que pode dobrar, mas não pode esticar. À medida que sua proporção diminui em direção a , todas as incorporações suaves parecem se aproximar da mesma forma triangular.${\displaystyle {\sqrt {3}}\approx 1,73}$${\displaystyle {\sqrt {3}}}$

As dobras longitudinais de uma tira Möbius plana dobrada em sanfona impedem que ela forme um encaixe tridimensional em que as camadas são separadas umas das outras e dobram suavemente sem amassar ou se afastar das dobras. Em vez disso, ao contrário do caso dobrado plano, há um limite inferior para a proporção de tiras Möbius retangulares lisas. Sua proporção de aspecto não pode ser menor que , mesmo se auto-interseções forem permitidas. Faixas de Möbius lisas de auto-interseção existem para qualquer proporção acima desse limite. Sem auto-interseções, a proporção deve ser pelo menos${\estilo de exibição \pi /2\aprox 1,57}$

$${\displaystyle {\frac {2{\sqrt {4-2{\sqrt {3}}}}+4}{{\sqrt {2{\sqrt {3}}}}+2{\sqrt {2{ \sqrt {3}}-3}}}}\approx 1.695.}$$

Para proporções entre este limite e , não se sabe se ${\displaystyle {\sqrt {3}}}$existem incorporações suaves, sem auto-interseção . Se o requisito de suavidade for relaxado para permitir superfícies continuamente diferenciáveis , o teorema de Nash-Kuiper implica que quaisquer duas arestas opostas de qualquer retângulo podem ser coladas para formar uma faixa de Möbius embutida, não importa quão pequena a razão de aspecto se torne. O caso limite, uma superfície obtida a partir de uma faixa infinita do plano entre duas linhas paralelas, coladas com orientação oposta uma à outra, é chamada de faixa de Möbius ilimitada ou feixe de linhas tautológicas reais . Embora não tenha um encaixe suave no espaço tridimensional, ele pode ser incorporado suavemente no espaço euclidiano quadridimensional .

A forma de energia mínima de uma tira de Möbius lisa colada a partir de um retângulo não tem uma descrição analítica conhecida, mas pode ser calculada numericamente, e tem sido objeto de muitos estudos na teoria das placas desde o trabalho inicial sobre este assunto em 1930 por Michael Sadowsky . Também é possível encontrar superfícies algébricas que contêm tiras de Möbius retangulares desenvolvíveis .

Fazendo a fronteira circular

Colando duas tiras de Möbius para formar uma garrafa de Klein

Uma projeção da faixa de Möbius sudanesa

A borda, ou limite , de uma faixa de Möbius é topologicamente equivalente a um círculo . Nas formas comuns da faixa de Möbius, ela tem uma forma diferente de um círculo, mas é sem nós e, portanto, toda a faixa pode ser esticada sem se cruzar para tornar a borda perfeitamente circular. Um desses exemplos é baseado na topologia da garrafa de Klein , uma superfície unilateral sem limite que não pode ser embutida no espaço tridimensional, mas pode ser imersa (permitindo que a superfície se cruze de certas maneiras restritas). Uma garrafa de Klein é a superfície que resulta quando duas tiras de Möbius são coladas de ponta a ponta e – invertendo esse processo – uma garrafa de Klein pode ser cortada ao longo de um corte cuidadosamente escolhido para produzir duas tiras de Möbius. Para uma forma da garrafa de Klein conhecida como garrafa de Klein de Lawson, a curva ao longo da qual ela é cortada pode ser circular, resultando em tiras de Möbius com bordas circulares.

A garrafa de Klein de Lawson é uma superfície mínima auto-cruzada na hiperesfera unitária do espaço 4-dimensional, o conjunto de pontos da forma

$${\displaystyle (\cos \theta \cos \phi ,\sin \theta \cos \phi ,\cos 2\theta \sin \phi ,\sin 2\theta \sin \phi )}$$

${\displaystyle 0\leq \theta <\pi ,0\leq \phi <2\pi }$

${\displaystyle 0\leq \phi <\pi }$

${\ displaystyle \ mathrm {O} (2)}$

Representação esquemática de uma tampa cruzada com um fundo aberto, mostrando seus conjuntos de nível . Esta superfície se cruza ao longo do segmento de linha vertical.

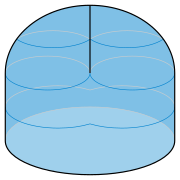
A faixa sudanesa de Möbius estende-se por todos os lados do seu círculo limítrofe, inevitavelmente para evitar que a superfície se cruze. Outra forma da tira de Möbius, chamada de cross-cap ou crosscap , também possui um limite circular, mas permanece apenas em um lado do plano desse círculo, tornando-o mais conveniente para fixação em orifícios circulares em outras superfícies. Para tanto, ele se cruza. Ele pode ser formado removendo um quadrilátero do topo de um hemisfério, orientando as bordas do quadrilátero em direções alternadas e, em seguida, colando pares opostos dessas bordas consistentemente com essa orientação. As duas partes da superfície formadas pelos dois pares de arestas coladas se cruzam com um ponto de pinçamento semelhante ao de um guarda- chuva de Whitney em cada extremidade do segmento de cruzamento, a mesma estrutura topológica vista no conóide de Plücker .

Superfícies de curvatura constante

A faixa de Möbius aberta é o interior relativo de uma faixa de Möbius padrão, formada pela omissão dos pontos em sua borda limítrofe. Pode ser dada uma geometria Riemanniana de curvatura Gaussiana positiva, negativa ou zero constante . Os casos de curvatura negativa e zero formam superfícies geodésicas completas, o que significa que todas as geodésicas ("linhas retas" na superfície) podem ser estendidas indefinidamente em qualquer direção.

Curvatura zero

Uma tira aberta com curvatura zero pode ser construída colando os lados opostos de uma tira plana entre duas linhas paralelas, descritas acima como o feixe de linhas tautológicas . A métrica resultante torna a faixa de Möbius aberta em uma superfície plana (geodesicamente) completa (ou seja, com curvatura gaussiana zero em todos os lugares). Esta é a métrica única na faixa de Möbius, até escala uniforme, que é plana e completa. É o espaço quociente de um plano por uma reflexão de deslizamento , e (junto com o plano, cilindro , toro e garrafa de Klein ) é uma das cinco variedades planas completas bidimensionais .

Curvatura negativa

A tira de Möbius aberta também admite métrica completa de curvatura negativa constante. Uma maneira de ver isso é começar com o modelo de meio plano superior (Poincaré) do plano hiperbólico , uma geometria de curvatura constante cujas linhas são representadas no modelo por semicírculos que encontram o eixo - em ângulos retos. Pegue o subconjunto do semiplano superior entre quaisquer dois semicírculos aninhados e identifique o semicírculo externo com a inversão esquerda-direita do semicírculo interno. O resultado é topologicamente uma tira de Möbius completa e não compacta com curvatura negativa constante. É uma superfície hiperbólica completa "não padronizada" no sentido de que contém um semiplano hiperbólico completo (na verdade dois, em lados opostos do eixo de reflexão de deslizamento), e é uma das apenas 13 superfícies não padronizadas. Novamente, isso pode ser entendido como o quociente do plano hiperbólico por uma reflexão de deslizamento.${\estilo de exibição x}$

Curvatura positiva

Uma faixa de Möbius de curvatura positiva constante não pode ser completa, pois sabe-se que as únicas superfícies completas de curvatura positiva constante são a esfera e o plano projetivo . No entanto, em certo sentido, está a apenas um ponto de ser uma superfície completa, pois a faixa de Möbius aberta é homeomorfa ao plano projetivo uma vez perfurado, a superfície obtida pela remoção de qualquer ponto do plano projetivo.

As superfícies mínimas são descritas como tendo curvatura média zero constante em vez de curvatura gaussiana constante. A faixa de Möbius sudanesa foi construída como uma superfície mínima limitada por um grande círculo em uma esfera de 3, mas também há uma superfície mínima completa (sem limites) imersa no espaço euclidiano que tem a topologia de uma faixa de Möbius aberta. É chamado de tira Meeks Möbius, após sua descrição de 1982 por William Hamilton Meeks, III . Embora globalmente instável como uma superfície mínima, pequenos trechos dela, delimitados por curvas não contráteis dentro da superfície, podem formar faixas de Möbius embutidas estáveis ​​como superfícies mínimas. Tanto a faixa de Meeks Möbius, quanto todas as superfícies mínimas de dimensão superior com a topologia da faixa de Möbius, podem ser construídas usando soluções para o problema de Björling , que define uma superfície mínima exclusivamente a partir de sua curva limite e planos tangentes ao longo dessa curva.

Espaços de linhas

A família de linhas no plano pode receber a estrutura de um espaço suave, com cada linha representada como um ponto neste espaço. O espaço de linhas resultante é topologicamente equivalente à faixa de Möbius aberta . Uma maneira de ver isso é estender o plano euclidiano para o plano projetivo real adicionando mais uma linha, a linha no infinito . Por dualidade projetiva o espaço de linhas no plano projetivo é equivalente ao seu espaço de pontos, o próprio plano projetivo. Retirar a linha no infinito, para produzir o espaço das linhas euclidianas, perfura esse espaço das linhas projetivas. Portanto, o espaço das linhas euclidianas é um plano projetivo perfurado, que é uma das formas da faixa de Möbius aberta. O espaço de linhas no plano hiperbólico pode ser parametrizado por pares não ordenados de pontos distintos em um círculo, os pares de pontos no infinito de cada linha. Este espaço, novamente, tem a topologia de uma faixa de Möbius aberta.

Esses espaços de linhas são altamente simétricos. As simetrias das linhas euclidianas incluem as transformações afins , e as simetrias das linhas hiperbólicas incluem as transformações de Möbius . As transformações afins e as transformações de Möbius formam grupos de Lie 6-dimensionais , espaços topológicos com uma estrutura algébrica compatível que descreve a composição das simetrias. Como todas as linhas do plano são simétricas a todas as outras linhas, a faixa de Möbius aberta é um espaço homogêneo , um espaço com simetrias que levam todos os pontos a todos os outros pontos. Espaços homogêneos de grupos de Lie são chamados de variedades solv , e a faixa de Möbius pode ser usada como contra -exemplo , mostrando que nem toda variedade solv é uma variedade nil , e que nem toda variedade solv pode ser fatorada em um produto direto de uma variedade solv compacta com . Essas simetrias também fornecem outra maneira de construir a própria faixa de Möbius, como um modelo de grupo desses grupos de Lie. Um modelo de grupo consiste em um grupo Lie e um subgrupo estabilizador de sua ação; contrair os cosets do subgrupo para pontos produz um espaço com a mesma topologia que o espaço homogêneo subjacente. No caso das simetrias de linhas euclidianas, o estabilizador do -eixo consiste em todas as simetrias que levam o eixo para si. Cada linha corresponde a um coset, o conjunto de simetrias que mapeiam para o -eixo. Portanto, o espaço quociente , um espaço que tem um ponto por coset e herda sua topologia do espaço de simetrias, é o mesmo que o espaço de linhas, e é novamente uma faixa de Möbius aberta.${\displaystyle \mathbb {R} ^{n}}$${\estilo de exibição x}$${\estilo de exibição \ell}$${\estilo de exibição \ell}$${\estilo de exibição x}$

Formulários

Fluxo elétrico em um resistor de Möbius

Além das já discutidas aplicações das tiras Möbius para o desenho de correias mecânicas que se desgastam uniformemente em toda a sua superfície, e do conóide Plücker para o projeto de engrenagens, outras aplicações das tiras Möbius incluem:

• Fitas de grafeno torcidas para formar tiras de Möbius com novas características eletrônicas, incluindo magnetismo helicoidal
• A aromaticidade de Möbius , uma propriedade de produtos químicos orgânicos cuja estrutura molecular forma um ciclo, com orbitais moleculares alinhados ao longo do ciclo no padrão de uma faixa de Möbius
• O resistor de Möbius , uma tira de material condutor que cobre o lado único de uma tira de Möbius dielétrica , de uma forma que cancela sua própria auto-indutância
• Ressonadores com um design compacto e uma frequência de ressonância que é metade das bobinas lineares construídas de forma idêntica
• Padrões de polarização na luz emergindo de uma placa q
• Uma prova da impossibilidade de regras de agregação bipartidária contínuas, anônimas e unânimes na teoria da escolha social
• Montanha-russa Möbius loop , uma forma de montanha-russa de pista dupla em que as duas pistas giram em torno uma da outra um número ímpar de vezes, de modo que os vagões retornam para a outra pista do que aquela em que começaram
• Mapas-múndi projetados em uma faixa de Möbius com as propriedades convenientes de que não há limites leste-oeste e que o antípoda de qualquer ponto do mapa pode ser encontrado no outro lado impresso da superfície no mesmo ponto da faixa de Möbius

Os cientistas também estudaram a energética de filmes de sabão em forma de tiras de Möbius, a síntese química de moléculas com forma de tira de Möbius e a formação de tiras de Möbius em nanoescala maiores usando origami de DNA .

Na cultura popular

Endless Twist , Max Bill , 1956, do Museu de Esculturas ao Ar Livre de Middelheim

As obras de arte bidimensionais com a tira de Möbius incluem uma pintura sem título de 1947 de Corrado Cagli (memorializada em um poema de Charles Olson ) e duas gravuras de MC Escher : Möbius Band I (1961), representando três peixes chatos dobrados mordendo as caudas uns dos outros; e Möbius Band II (1963), retratando formigas rastejando em torno de uma faixa de Möbius em forma de lemniscata . É também um tema popular da escultura matemática , incluindo obras de Max Bill ( Fita sem fim , 1953), José de Rivera ( Infinito , 1967) e Sebastián . Uma tira de Möbius com nó de trevo foi usada em Imortalidade de John Robinson ( 1982). Charles O. Perry 's Continuum (1976) é uma das várias peças de Perry explorando variações da tira de Möbius.

Símbolo de reciclagem

Logotipo do Google Drive (2012–2014)

Logo do IMPA no selo

Devido à sua forma facilmente reconhecível, as tiras de Möbius são um elemento comum do design gráfico . O familiar logotipo de três setas para reciclagem , projetado em 1970, é baseado na forma triangular suave da faixa de Möbius, assim como o logotipo da Expo '74 com tema ambiental . Algumas variações do símbolo de reciclagem usam uma incorporação diferente com três meias torções em vez de uma, e a versão original do logotipo do Google Drive usava uma tira Möbius de três torções dobrada, assim como outros designs semelhantes. O Instituto Nacional de Matemática Pura e Aplicada (IMPA) usa uma tira de Möbius estilizada e lisa como seu logotipo e tem uma grande escultura correspondente de uma tira de Möbius em exibição em seu prédio. A tira de Möbius também apareceu na arte de selos postais de países como Brasil, Bélgica, Holanda e Suíça.

Entrada do Hall da Fama da NASCAR

As tiras de Möbius têm sido uma inspiração frequente para o projeto arquitetônico de edifícios e pontes. No entanto, muitos deles são projetos ou projetos conceituais em vez de objetos construídos, ou estendem sua interpretação da faixa de Möbius além de sua reconhecibilidade como uma forma matemática ou uma parte funcional da arquitetura. Um exemplo é a Biblioteca Nacional do Cazaquistão , para a qual um edifício foi planejado na forma de uma faixa de Möbius espessa, mas refeito com um design diferente depois que os arquitetos originais desistiram do projeto. Um edifício notável que incorpora uma faixa de Möbius é o Hall da Fama da NASCAR , que é cercado por uma grande fita torcida de aço inoxidável atuando como fachada e cobertura, evocando as formas curvas das pistas de corrida. Em menor escala, a Cadeira Moebius (2006) de Pedro Reyes é um banco de cortejo cuja base e laterais têm a forma de uma faixa de Möbius. Como forma de matemática e artes de fibra , os lenços foram tricotados em tiras de Möbius desde o trabalho de Elizabeth Zimmermann no início dos anos 80. No estilo de alimentos , as tiras de Möbius têm sido usadas para fatiar bagels , fazer laços de bacon e criar novas formas para massas .

Embora matematicamente a faixa de Möbius e a quarta dimensão sejam conceitos puramente espaciais, eles têm sido frequentemente invocados na ficção especulativa como base para um loop temporal no qual vítimas incautas podem ficar presas. Exemplos desse tropo incluem "No-Sided Professor" de Martin Gardner (1946), " A Subway Named Mobius " de Armin Joseph Deutsch (1950) e o filme Moebius (1996) baseado nele. Um mundo inteiro em forma de tira de Möbius é o cenário de "The Wall of Darkness" (1946) de Arthur C. Clarke , enquanto as tiras convencionais de Möbius são usadas como invenções inteligentes em várias histórias de William Hazlett Upson da década de 1940. Outras obras de ficção foram analisadas como tendo uma estrutura tipo tira de Möbius, na qual elementos da trama se repetem com uma reviravolta; Entre eles estão In Search of Lost Time (1913-1927), de Marcel Proust , Six Characters in Search of an Author (1921) , de Luigi Pirandello , It 's a Wonderful Life (1946) , de Frank Capra , Lost in the Funhouse (1968), Samuel R. Delany 's Dhalgren (1975 ) e o filme Donnie Darko (2001).

Um dos cânones musicais de JS Bach , o quinto dos 14 cânones ( BWV 1087 ) descoberto em 1974 na cópia de Bach das Variações Goldberg , apresenta uma simetria glide-reflect na qual cada voz do cânone repete, com notas invertidas , o mesmo motivo de duas medidas anteriores. Por causa dessa simetria, esse cânone pode ser pensado como tendo sua partitura escrita em uma tira de Möbius. Na teoria musical , tons que diferem por uma oitava são geralmente considerados notas equivalentes, e o espaço de notas possíveis forma um círculo, o círculo cromático . Como a faixa de Möbius é o espaço de configuração de dois pontos não ordenados em um círculo, o espaço de todos os acordes de duas notas toma a forma de uma faixa de Möbius. Esta concepção, e generalizações para mais pontos, é uma aplicação significativa de orbifolds à teoria musical . Grupos musicais modernos que levam seu nome da tira de Möbius incluem o trio de rock eletrônico americano Mobius Band e a banda de rock progressivo norueguesa Ring Van Möbius .

As tiras de Möbius e suas propriedades foram usadas no design da magia do palco . Um desses truques, conhecido como bandas afegãs, usa o fato de que a tira de Möbius permanece uma única tira quando cortada longitudinalmente. Originou-se na década de 1880 e foi muito popular na primeira metade do século XX. Muitas versões deste truque existem e foram realizadas por ilusionistas famosos como Harry Blackstone Sr. e Thomas Nelson Downs .

Veja também

• Contador de Möbius , um registrador de deslocamento cujo bit de saída é complementado antes de ser realimentado no bit de entrada
• Triângulo de Penrose , uma figura impossível cuja fronteira parece envolvê-lo em uma faixa de Möbius
• Teoria da fita , a teoria matemática de tiras infinitesimalmente finas que seguem curvas de espaço com nós
• Atrator de Smale-Williams , um fractal formado pelo espessamento repetido de uma curva espacial para uma faixa de Möbius e, em seguida, substituindo-a pela borda do limite
• Toro umbílico , uma forma tridimensional com seu limite formado por uma faixa de Möbius, colado a si mesmo ao longo de sua única borda

Notas

Referências

links externos

• Weisstein, Eric W. "Möbius Strip" . MathWorld .