Ladrilhos triangulares - Triangular tiling

Ladrilhos triangulares
Modelo	Ladrilhos regulares
Configuração do vértice	3.3.3.3.3.3 (ou 3 6 )
Configuração de rosto	V6.6.6 (ou V6 3 )
Símbolo (s) Schläfli	{3,6} {3 [3] }
Símbolo (s) Wythoff	6 3 2 3 | 3 3 | 3 3 3
Diagrama (s) de Coxeter	=
Simetria	p6m , [6,3], (* 632)
Simetria de rotação	p6 , [6,3] + , (632) p3 , [3 [3] ] + , (333)
Dual	Ladrilhos hexagonais
Propriedades	Vertex-transitivo , edge-transitivo , face-transitivo

Na geometria , o mosaico triangular ou tessellation triangular é um dos três regulares pavimentações do plano euclidiano , e é a única tal ladrilhos onde as formas constitutivas não são parallelogons . Como o ângulo interno do triângulo equilátero é de 60 graus, seis triângulos em um ponto ocupam 360 graus completos. A telha triangular tem o símbolo Schläfli de {3,6}.

Conway o chama de deltille , nomeado a partir da forma triangular da letra grega delta (Δ). O ladrilho triangular também pode ser chamado de kishextille por uma operação kis que adiciona um ponto central e triângulos para substituir as faces de um hextille .

É uma das três curvas regulares do avião . Os outros dois são os ladrilhos quadrados e os hexagonais .

Colorações uniformes

Uma telha triangular de 2 uniformes, 4 triângulos coloridos, relacionados ao poliedro geodésico como {3,6+} _2,0 .

Existem 9 colorações uniformes distintas de uma telha triangular. (Nomeando as cores por índices nos 6 triângulos em torno de um vértice: 111111, 111112, 111212, 111213, 111222, 112122, 121212, 121213, 121314) Três deles podem ser derivados de outros repetindo cores: 111212 e 111112 de 121213 por combinando 1 e 3, enquanto 111213 é reduzido de 121314.

Há uma classe de colorações arquimedianas , 111112, (marcada com um *) que não é uniforme, contendo fileiras alternadas de triângulos onde cada terço é colorido. O exemplo mostrado é 2-uniforme, mas há infinitas cores arquimedianas que podem ser criadas por deslocamentos horizontais arbitrários das linhas.

111111	121212	111222	112122	111112 (*)
p6m (* 632)	p3m1 (* 333)	cmm (2 * 22)	p2 (2222)	p2 (2222)

121213	111212	111112	121314	111213
p31m (3 * 3)			p3 (333)

Malha A2 e embalagens de círculo

O A^*
₂ treliça como três telhas triangulares: + +

O arranjo do vértice da telha triangular é chamado _de rede A ₂ . É o caso bidimensional de um favo de mel simples .

O A^*
₂ treliça (também chamada de A³
₂) pode ser construída pela união de todas as três redes A ₂ e equivalente à rede A ₂ .

+ + = dual de =

Os vértices do ladrilho triangular são os centros do empacotamento circular mais denso possível . Cada círculo está em contato com 6 outros círculos na embalagem ( número de beijo ). A densidade de empacotamento é π ⁄ √ 12 ou 90,69%. A célula voronoi de uma telha triangular é um hexágono e, portanto, a tesselação de voronoi , a telha hexagonal, tem uma correspondência direta com as embalagens circulares.

Variações geométricas

Ladrilhos triangulares podem ser feitos com a topologia {3,6} equivalente ao ladrilho regular (6 triângulos ao redor de cada vértice). Com faces idênticas ( transitividade de face ) e transitividade de vértice , existem 5 variações. A simetria fornecida assume que todas as faces são da mesma cor.

• 

  
  Simetria p2 do triângulo escaleno

• 

  
  Simetria pmg do triângulo escaleno

• 

  
  Simetria cmm do triângulo isósceles

• 

  
  Simetria cmm do triângulo retângulo

• 

  
  Simetria p6m do triângulo equilateral

Poliedros e telhas relacionados

As telhas planas estão relacionadas aos poliedros . Colocar menos triângulos em um vértice deixa uma lacuna e permite que ele seja dobrado em uma pirâmide . Eles podem ser expandidos para sólidos platônicos : cinco, quatro e três triângulos em um vértice definem um icosaedro , octaedro e tetraedro, respectivamente.

Esta telha é topologicamente relacionada como uma parte da sequência de poliedros regulares com símbolos Schläfli {3, n}, continuando no plano hiperbólico .

* n mutação de simetria 32 de tilings regulares: {3, n } v t e
Esférico				Euclides.	Hiper compacto.		Paraco.	Hiperbólica não compacta
3,3	3 3	3 4	3 5	3 6	3 7	3 8	3 ∞	3 12i	3 9i	3 6i	3 3i

Também está topologicamente relacionado como uma parte da sequência de sólidos catalães com configuração de face Vn.6.6, e também continua no plano hiperbólico.

V3.6.6

V4.6.6

V5.6.6

V6.6.6

V7.6.6

Construções Wythoff de ladrilhos hexagonais e triangulares

Como os poliedros uniformes, há oito ladrilhos uniformes que podem ser baseados nos ladrilhos hexagonais regulares (ou nos ladrilhos triangulares duplos).

Desenhando os ladrilhos coloridos de vermelho nas faces originais, amarelo nos vértices originais e azul ao longo das bordas originais, existem 8 formas, 7 que são topologicamente distintas. (O ladrilho triangular truncado é topologicamente idêntico ao ladrilho hexagonal.)

Ladrilhos hexagonais / triangulares uniformes
Domínios Fundamentais	Simetria : [6,3], (* 632)							[6,3] + , (632)
	{6,3}	t {6,3}	r {6,3}	t {3,6}	{3,6}	rr {6,3}	tr {6,3}	sr {6,3}
Config.	6 3	3.12.12	(6,3) 2	6.6.6	3 6	3.4.6.4	4.6.12	3.3.3.3.6

Telhas de simetria triangular v t e
Wythoff	3 | 3 3	3 3 | 3	3 | 3 3	3 3 | 3	3 | 3 3	3 3 | 3	3 3 3 |	| 3 3 3
Coxeter
Imagem Vertex figura	(3,3) 3	3.6.3.6	(3,3) 3	3.6.3.6	(3,3) 3	3.6.3.6	6.6.6	3.3.3.3.3.3

Apeirogons complexos regulares relacionados

Existem 4 apeirogons complexos regulares , compartilhando os vértices da telha triangular. Apeirogons complexos regulares têm vértices e arestas, onde as arestas podem conter 2 ou mais vértices. Apeirogons regulares p { q } r são restringidos por: 1 / p + 2 / q + 1 / r = 1. As arestas têm vértices p e as figuras dos vértices são r -gonal.

O primeiro é feito de 2 arestas, e as próximas duas são arestas triangulares, e a última tem arestas hexagonais sobrepostas.

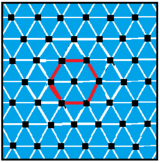
2 {6} 6 ou	3 {4} 6 ou	3 {6} 3 ou	6 {3} 6 ou

Outras telhas triangulares

Existem também três ladrilhos Laves feitos de um único tipo de triângulos:

Kisrhombille 30 ° -60 ° -90 ° triângulos retângulos

Kisquadrille 45 ° -45 ° -90 ° triângulos retângulos

Triângulos isósceles de 30 ° -30 ° -120 ° Kisdeltile

Veja também

• Favo de mel de ladrilhos triangulares
• Favo de mel simplético
• Tilings de polígonos regulares
• Lista de peças uniformes
• Isogrid (projeto estrutural usando azulejos triangulares)

Referências

• Coxeter, HSM Regular Polytopes , (3ª edição, 1973), edição Dover, ISBN  0-486-61480-8 p. 296, Tabela II: Favos de mel regulares
• Grünbaum, Branko & Shephard, GC (1987). Tilings e padrões . Nova York: WH Freeman. ISBN 0-7167-1193-1.(Capítulo 2.1: Ladrilhos regulares e uniformes , págs. 58-65, Capítulo 2.9 Colorações arquimedianas e uniformes, págs. 102-107)
• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design . Dover Publications, Inc. ISBN 0-486-23729-X. p35
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN  978-1-56881-220-5 [1]

links externos

• Weisstein, Eric W. "Triangular Grid" . MathWorld .
  • Weisstein, Eric W. "Tessellation regular" . MathWorld .
  • Weisstein, Eric W. "Uniform tessellation" . MathWorld .
• Klitzing, Richard. "Telhas euclidianas 2D x3o6o - trat - O2" .

v t e Favos de mel fundamentais convexos regulares e uniformes nas dimensões 2-9
Espaço	Família	${\ displaystyle {\ tilde {A}} _ {n-1}}$	${\ displaystyle {\ tilde {C}} _ ​​{n-1}}$	${\ displaystyle {\ tilde {B}} _ {n-1}}$	${\ displaystyle {\ tilde {D}} _ {n-1}}$	${\ displaystyle {\ tilde {G}} _ {2}}$/ /${\ displaystyle {\ tilde {F}} _ {4}}$${\ displaystyle {\ tilde {E}} _ {n-1}}$
E 2	Ladrilhos uniformes	{3 [3] }	δ 3	hδ 3	qδ 3	Hexagonal
E 3	Favo de mel convexo uniforme	{3 [4] }	δ 4	hδ 4	qδ 4
E 4	4-favo de mel uniforme	{3 [5] }	δ 5	hδ 5	qδ 5	Favo de mel de 24 células
E 5	Uniforme 5-favo de mel	{3 [6] }	δ 6	hδ 6	qδ 6
E 6	Uniforme 6-favo de mel	{3 [7] }	δ 7	hδ 7	qδ 7	2 22
E 7	Uniforme 7-favo de mel	{3 [8] }	δ 8	hδ 8	qδ 8	1 33 • 3 31
E 8	Favo de mel 8 uniforme	{3 [9] }	δ 9	hδ 9	qδ 9	1 52 • 2 51 • 5 21
E 9	Uniforme 9-favo de mel	{3 [10] }	δ 10	hδ 10	qδ 10
E 10	Uniforme 10-favo de mel	{3 [11] }	δ 11	hδ 11	qδ 11
E n -1	Uniforme ( n -1) - favo de mel	{3 [n] }	δ n	hδ n	qδ n	1 k2 • 2 k1 • k 21