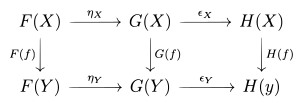Transformação natural - Natural transformation

Na teoria das categorias , um ramo da matemática , uma transformação natural fornece uma maneira de transformar um functor em outro, respeitando a estrutura interna (isto é, a composição dos morfismos ) das categorias envolvidas. Portanto, uma transformação natural pode ser considerada um "morfismo de functores". Na verdade, essa intuição pode ser formalizada para definir as chamadas categorias de functor . As transformações naturais são, depois de categorias e functores, uma das noções mais fundamentais da teoria das categorias e, conseqüentemente, aparecem na maioria de suas aplicações.

Definição

Se e são functores entre as categorias e , então uma transformação natural de para é uma família de morfismos que satisfaz dois requisitos. ${\ displaystyle F}$${\ displaystyle G}$${\ displaystyle C}$${\ displaystyle D}$ ${\ displaystyle \ eta}$${\ displaystyle F}$${\ displaystyle G}$

1. A transformação natural deve associar, a todo objeto em , um morfismo entre objetos de . O morfismo é chamado de componente de at .${\ displaystyle X}$${\ displaystyle C}$ ${\ displaystyle \ eta _ {X}: F (X) \ a G (X)}$${\ displaystyle D}$${\ displaystyle \ eta _ {X}}$${\ displaystyle \ eta}$${\ displaystyle X}$
2. Componentes deve ser tal que, para cada morfismo em que temos:${\ displaystyle f: X \ a Y}$${\ displaystyle C}$

${\ displaystyle \ eta _ {Y} \ circ F (f) = G (f) \ circ \ eta _ {X}}$

A última equação pode ser convenientemente expressa pelo diagrama comutativo

Se e forem contravariantes , as setas verticais neste diagrama são invertidas. Se é uma transformação natural de para , também escrevemos ou . Isso também é expresso dizendo que a família de morfismos é natural em . ${\ displaystyle F}$${\ displaystyle G}$${\ displaystyle \ eta}$${\ displaystyle F}$${\ displaystyle G}$${\ displaystyle \ eta: F \ to G}$${\ displaystyle \ eta: F \ implica G}$${\ displaystyle \ eta _ {X}: F (X) \ a G (X)}$${\ displaystyle X}$

Se, para cada objeto em , o morfismo é um isomorfismo em , então é dito que é um${\ displaystyle X}$${\ displaystyle C}$${\ displaystyle \ eta _ {X}}$${\ displaystyle D}$${\ displaystyle \ eta}$ isomorfismo natural (ou às vezesequivalência naturalouisomorfismo de functores). Dois functoresesão chamadosnaturalmente isomórficosou simplesmenteisomórficosse existir um isomorfismo natural dea. ${\ displaystyle F}$${\ displaystyle G}$${\ displaystyle F}$${\ displaystyle G}$

Uma transformação infranatural de para é simplesmente uma família de morfismos , para todos em . Assim, uma transformação natural é uma transformação infranatural para a qual para cada morfismo . O naturalizador de , nat , é a maior subcategoria de conter todos os objetos de sobre os quais se restringe a uma transformação natural. ${\ displaystyle \ eta}$${\ displaystyle F}$${\ displaystyle G}$${\ displaystyle \ eta _ {X}: F (X) \ a G (X)}$${\ displaystyle X}$${\ displaystyle C}$${\ displaystyle \ eta _ {Y} \ circ F (f) = G (f) \ circ \ eta _ {X}}$${\ displaystyle f: X \ a Y}$${\ displaystyle \ eta}$${\ displaystyle (\ eta)}$${\ displaystyle C}$${\ displaystyle C}$${\ displaystyle \ eta}$

Exemplos

Grupo oposto

Declarações como

"Cada grupo é naturalmente isomórfico ao seu grupo oposto "

abundam em matemática moderna. Daremos agora o significado preciso dessa afirmação, bem como sua prova. Considere a categoria de todos os grupos com homomorfismos de grupo como morfismos. Se for um grupo, definimos seu grupo oposto da seguinte forma: é o mesmo conjunto que , e a operação é definida por . Todas as multiplicações em são, portanto, "invertidas". Formar o grupo oposto torna-se um functor (covariante) de a se definirmos para qualquer homomorfismo de grupo . Observe que é de fato um homomorfismo de grupo de a : ${\ displaystyle {\ textbf {Grp}}}$${\ displaystyle (G, *)}$${\ displaystyle (G ^ {\ text {op}}, {*} ^ {\ text {op}})}$${\ displaystyle G ^ {\ text {op}}}$${\ displaystyle G}$${\ displaystyle * ^ {\ text {op}}}$${\ displaystyle a * ^ {\ text {op}} b = b * a}$${\ displaystyle G ^ {\ text {op}}}$${\ displaystyle {\ textbf {Grp}}}$${\ displaystyle {\ textbf {Grp}}}$${\ displaystyle f ^ {\ text {op}} = f}$${\ displaystyle f: G \ a H}$${\ displaystyle f ^ {\ text {op}}}$${\ displaystyle G ^ {\ text {op}}}$${\ displaystyle H ^ {\ text {op}}}$

${\ displaystyle f ^ {\ text {op}} (a * ^ {\ text {op}} b) = f (b * a) = f (b) * f (a) = f ^ {\ text {op }} (a) * ^ {\ text {op}} f ^ {\ text {op}} (b).}$

O conteúdo da declaração acima é:

"O functor de identidade é naturalmente isomórfico ao functor oposto "${\ displaystyle {\ text {Id}} _ {\ textbf {Grp}}: {\ textbf {Grp}} \ to {\ textbf {Grp}}}$${\ displaystyle {\ text {op}}: {\ textbf {Grp}} \ to {\ textbf {Grp}}}$

Para provar isso, precisamos fornecer isomorfismos para cada grupo , de forma que o diagrama acima comute. Definir . As fórmulas e mostram que é um homomorfismo de grupo com inverso . Para comprovar a naturalidade, partimos de um homomorfismo de grupo e mostramos , ou seja, para todos dentro . Isso é verdade porque e todo homomorfismo de grupo tem a propriedade . ${\ displaystyle \ eta _ {G}: G \ para G ^ {\ text {op}}}$${\ displaystyle G}$${\ displaystyle \ eta _ {G} (a) = a ^ {- 1}}$${\ displaystyle (a * b) ^ {- 1} = b ^ {- 1} * a ^ {- 1} = a ^ {- 1} * ^ {\ text {op}} b ^ {- 1}}$${\ displaystyle (a ^ {- 1}) ^ {- 1} = a}$${\ displaystyle \ eta _ {G}}$${\ displaystyle \ eta _ {G ^ {\ text {op}}}}$${\ displaystyle f: G \ a H}$${\ displaystyle \ eta _ {H} \ circ f = f ^ {\ text {op}} \ circ \ eta _ {G}}$${\ displaystyle (f (a)) ^ {- 1} = f ^ {\ text {op}} (a ^ {- 1})}$${\ displaystyle a}$${\ displaystyle G}$${\ displaystyle f ^ {\ text {op}} = f}$${\ displaystyle (f (a)) ^ {- 1} = f (a ^ {- 1})}$

Abelianização

Dado um grupo , podemos definir sua abelianização . Vamos denotar o mapa de projeção nos cosets de . Este homomorfismo é "natural em ", ou seja, define uma transformação natural, que agora verificamos. Deixe ser um grupo. Para qualquer homomorfismo , temos que está contido no kernel de , porque qualquer homomorfismo em um grupo abeliano mata o subgrupo do comutador. Em seguida, fatore como para o homomorfismo único . Isso cria um functor e uma transformação natural, mas não um isomorfismo natural, do functor de identidade para . ${\ displaystyle G}$ ${\ displaystyle G ^ {\ text {ab}} = G /}$ ${\ displaystyle [G, G]}$${\ displaystyle \ pi _ {G}: G \ para G ^ {\ text {ab}}}$${\ displaystyle [G, G]}$${\ displaystyle G}$${\ displaystyle H}$${\ displaystyle f: G \ a H}$${\ displaystyle [G, G]}$${\ displaystyle \ pi _ {H} \ circ f}$${\ displaystyle \ pi _ {H} \ circ f}$${\ displaystyle G ^ {\ text {ab}}}$${\ displaystyle f ^ {\ text {ab}} \ circ \ pi _ {G} = \ pi _ {H} \ circ f}$${\ displaystyle f ^ {\ text {ab}}: G ^ {\ text {ab}} \ to H ^ {\ text {ab}}}$${\ displaystyle {\ text {ab}}: {\ textbf {Grp}} \ to {\ textbf {Grp}}}$${\ displaystyle \ pi}$${\ displaystyle {\ text {ab}}}$

Homomorfismo de Hurewicz

Funcionalidades e transformações naturais abundam na topologia algébrica , com os homomorfismos de Hurewicz servindo como exemplos. Para qualquer espaço topológico pontiagudo e inteiro positivo existe um homomorfismo de grupo${\ displaystyle (X, x)}$${\ displaystyle n}$

${\ displaystyle h _ {*} \ dois pontos \ pi _ {n} (X, x) \ a H_ {n} (X)}$

do -ésimo grupo de homotopia de ao -ésimo grupo de homologia de . Ambos e são functores da categoria Top ^* de espaços topológicos pontiagudos para a categoria Grp de grupos, e é uma transformação natural de para . ${\ displaystyle n}$${\ displaystyle (X, x)}$${\ displaystyle n}$${\ displaystyle X}$${\ displaystyle \ pi _ {n}}$${\ displaystyle H_ {n}}$${\ displaystyle h _ {*}}$${\ displaystyle \ pi _ {n}}$${\ displaystyle H_ {n}}$

Determinante

Dado anéis conmutativos e com um homomorphism anel , os respectivos grupos de inversíveis matrizes e herdar um homomorphism que denotam por , obtido pela aplicação de cada entrada de matriz. Da mesma forma, restringe-se a um homomorfismo de grupo , onde denota o grupo de unidades de . Na verdade, e são functores da categoria de anéis comutativos a . O determinante no grupo , denotado por , é um homomorfismo de grupo ${\ displaystyle R}$${\ displaystyle S}$ ${\ displaystyle f: R \ to S}$ ${\ displaystyle n \ times n}$${\ displaystyle {\ text {GL}} _ {n} (R)}$${\ displaystyle {\ text {GL}} _ {n} (S)}$${\ displaystyle {\ text {GL}} _ {n} (f)}$${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle f ^ {*}: R ^ {*} \ a S ^ {*}}$${\ displaystyle R ^ {*}}$${\ displaystyle R}$${\ displaystyle {\ text {GL}} _ {n}}$${\ displaystyle *}$${\ displaystyle {\ textbf {CRing}}}$${\ displaystyle {\ textbf {Grp}}}$${\ displaystyle {\ text {GL}} _ {n} (R)}$${\ displaystyle {\ text {det}} _ {R}}$

${\ displaystyle {\ mbox {det}} _ {R} \ colon {\ mbox {GL}} _ {n} (R) \ para R ^ {*}}$

que é natural em : porque o determinante é definido pela mesma fórmula para todos os anéis, é válido. Isso torna o determinante uma transformação natural de para . ${\ displaystyle R}$${\ displaystyle f \ circ {\ text {det}} _ {R} = {\ text {det}} _ {S} \ circ {\ text {GL}} _ {n} (f)}$${\ displaystyle {\ text {GL}} _ {n}}$${\ displaystyle *}$

Duplo duplo de um espaço vetorial

Se for um campo , então para cada espaço vetorial sobre nós temos um mapa linear injetivo "natural" do espaço vetorial em seu dual duplo . Esses mapas são "naturais" no seguinte sentido: a operação dual dual é um functor, e os mapas são os componentes de uma transformação natural do functor de identidade para o functor dual dual. ${\ displaystyle K}$ ${\ displaystyle V}$${\ displaystyle K}$ ${\ displaystyle V \ a V ^ {**}}$

Cálculo finito

Para cada grupo abeliano , o conjunto de funções dos inteiros para o conjunto subjacente de formas um grupo abeliano sob adição pontual. (Aqui está o functor esquecido padrão .) Dado um morfismo , o mapa dado pela composição da esquerda com os elementos do primeiro é em si um homomorfismo de grupos abelianos; desta forma, obtemos um functor . O operador de diferença finita que leva cada função para é um mapa de si mesmo, e a coleção de tais mapas fornece uma transformação natural . ${\ displaystyle G}$${\ displaystyle {\ text {Hom}} _ {\ textbf {Set}} (\ mathbb {Z}, U (G))}$${\ displaystyle G}$${\ displaystyle V _ {\ mathbb {Z}} (G)}$${\ displaystyle U}$ ${\ displaystyle U: {\ textbf {Ab}} \ to {\ textbf {Set}}}$${\ displaystyle {\ textbf {Ab}}}$${\ displaystyle \ varphi: G \ to G '}$${\ displaystyle V _ {\ mathbb {Z}} (\ varphi): V _ {\ mathbb {Z}} (G) \ a V _ {\ mathbb {Z}} (G ')}$${\ displaystyle \ varphi}$${\ displaystyle V _ {\ mathbb {Z}}: {\ textbf {Ab}} \ to {\ textbf {Ab}}}$${\ displaystyle \ Delta _ {G}}$${\ displaystyle f: \ mathbb {Z} \ to U (G)}$${\ displaystyle \ Delta (f): n \ mapsto f (n + 1) -f (n)}$${\ displaystyle V _ {\ mathbb {Z}} (G)}$${\ displaystyle \ Delta}$${\ displaystyle \ Delta: V _ {\ mathbb {Z}} \ a V _ {\ mathbb {Z}}}$

Adjunção Tensor-hom

Considere a categoria${\ displaystyle {\ textbf {Ab}}}$ de grupos abelianos e homomorfismos de grupo. Para todos os grupos abelianos , e temos um isomorfismo de grupo ${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle Z}$

${\ displaystyle {\ text {Hom}} (X \ otimes Y, Z) \ to {\ text {Hom}} (X, {\ text {Hom}} (Y, Z))}$.

Esses isomorfismos são "naturais" no sentido de que definem uma transformação natural entre os dois functores envolvidos . (Aqui, "op" é a categoria oposta de , não deve ser confundida com o functor de grupo oposto trivial em  !) ${\ displaystyle {\ textbf {Ab}} ^ {\ text {op}} \ times {\ textbf {Ab}} ^ {\ text {op}} \ times {\ textbf {Ab}} \ to {\ textbf { Ab}}}$${\ displaystyle {\ textbf {Ab}}}$${\ displaystyle {\ textbf {Ab}}}$

Este é formalmente o adjunção tensor-hom , e é um exemplo arquetípico de um par de functores adjuntos . Transformações naturais surgem freqüentemente em conjunto com functores adjuntos e, de fato, functores adjunto são definidos por um certo isomorfismo natural. Além disso, cada par de functores adjuntos vem equipado com duas transformações naturais (geralmente não isomorfismos) chamadas de unidade e contagem .

Isomorfismo não natural

A noção de uma transformação natural é categórica e afirma (informalmente) que um mapa específico entre functores pode ser feito de forma consistente em uma categoria inteira. Informalmente, um mapa particular (especialmente um isomorfismo) entre objetos individuais (não categorias inteiras) é referido como um "isomorfismo natural", significando implicitamente que é realmente definido em toda a categoria e define uma transformação natural de functores; formalizar essa intuição foi um fator motivador no desenvolvimento da teoria das categorias. Por outro lado, um mapa particular entre objetos particulares pode ser chamado de isomorfismo não natural (ou "este isomorfismo não é natural") se o mapa não pode ser estendido para uma transformação natural em toda a categoria. Dado um objeto, um functor (tomando por simplicidade o primeiro functor como a identidade) e uma prova de isomorfismo de não naturalidade é mais facilmente mostrada fornecendo um automorfismo que não comuta com esse isomorfismo (então ). Mais fortemente, se alguém deseja provar que e não são naturalmente isomórficos, sem referência a um isomorfismo particular, isso requer mostrar que para qualquer isomorfismo , há algum com o qual ele não comuta; em alguns casos, um único automorfismo funciona para todos os isomorfismos candidatos, enquanto em outros casos deve-se mostrar como construir um diferente para cada isomorfismo. Os mapas da categoria desempenham um papel crucial - qualquer transformação infranatural é natural se os únicos mapas forem o mapa de identidade, por exemplo. ${\ displaystyle X,}$${\ displaystyle G}$${\ displaystyle \ eta \ dois pontos X \ a G (X),}$${\ displaystyle A \ dois pontos X \ a X}$${\ displaystyle \ eta \ circ A \ neq G (A) \ circ \ eta}$${\ displaystyle X}$${\ displaystyle G (X)}$${\ displaystyle \ eta}$${\ displaystyle A}$${\ displaystyle A}$${\ displaystyle \ eta}$${\ displaystyle A _ {\ eta}}$

Isso é semelhante (mas mais categórico) aos conceitos da teoria dos grupos ou teoria dos módulos, onde uma dada decomposição de um objeto em uma soma direta "não é natural", ou melhor, "não é única", visto que existem automorfismos que não preservam o direto decomposição da soma - veja o teorema da estrutura para módulos gerados finitamente sobre um domínio ideal principal § Unicidade, por exemplo.

Alguns autores distinguem notacionalmente, usando para um isomorfismo natural e para um isomorfismo não natural, reservando para igualdade (geralmente igualdade de mapas). ${\ displaystyle \ cong}$${\ displaystyle \ aprox}$${\ displaystyle =}$

Exemplo: grupo fundamental de toro

Como um exemplo da distinção entre o enunciado funcional e objetos individuais, considere os grupos de homotopia de um espaço de produto, especificamente o grupo fundamental do toro.

Os grupos de homotopia de um espaço de produto são naturalmente o produto dos grupos de homotopia dos componentes, com o isomorfismo dado pela projeção sobre os dois fatores, fundamentalmente porque mapas em um espaço de produto são exatamente produtos de mapas em componentes - este é um funcional demonstração. ${\ displaystyle \ pi _ {n} ((X, x_ {0}) \ times (Y, y_ {0})) \ cong \ pi _ {n} ((X, x_ {0})) \ times \ pi _ {n} ((Y, y_ {0})),}$

No entanto, o toro (que é abstratamente um produto de dois círculos) tem um grupo fundamental isomorfo para , mas a divisão não é natural. Observe o uso de , e : ${\ displaystyle Z ^ {2}}$${\ displaystyle \ pi _ {1} (T, t_ {0}) \ approx \ mathbf {Z} \ times \ mathbf {Z}}$${\ displaystyle \ aprox}$${\ displaystyle \ cong}$${\ displaystyle =}$

${\ displaystyle \ pi _ {1} (T, t_ {0}) \ approx \ pi _ {1} (S ^ {1}, x_ {0}) \ times \ pi _ {1} (S ^ {1 }, y_ {0}) \ cong \ mathbf {Z} \ times \ mathbf {Z} = \ mathbf {Z} ^ {2}.}$

Este isomorfismo abstrato com um produto não é natural, pois alguns isomorfismos de não preservam o produto: o auto-homeomorfismo de (considerado como o espaço quociente ) dado por (geometricamente uma torção de Dehn sobre uma das curvas geradoras) atua como este matriz ligada (está no grupo linear geral de matrizes inteiras invertíveis), o que não preserva a decomposição como um produto porque não é diagonal. No entanto, se for dado o toro como um produto - equivalentemente, dada uma decomposição do espaço - então a divisão do grupo segue a afirmação geral anterior. Em termos categóricos, a categoria relevante (preservando a estrutura de um espaço de produto) é "mapas de espaços de produto, nomeadamente um par de mapas entre as respectivas componentes". ${\ displaystyle T}$${\ displaystyle T}$ ${\ displaystyle R ^ {2} / \ mathbb {Z} ^ {2}}$${\ displaystyle \ left ({\ begin {smallmatrix} 1 e 1 \\ 0 & 1 \ end {smallmatrix}} \ right)}$${\ displaystyle \ mathbb {Z} ^ {2}}$ ${\ displaystyle {\ text {GL}} (\ mathbb {Z}, 2)}$${\ displaystyle (T, t_ {0}) = (S ^ {1}, x_ {0}) \ times (S ^ {1}, y_ {0})}$

Naturalidade é uma noção categórica e requer ser muito preciso sobre exatamente quais dados são dados - o toro como um espaço que passa a ser um produto (na categoria de espaços e mapas contínuos) é diferente do toro apresentado como um produto (em a categoria de produtos de dois espaços e mapas contínuos entre as respectivas componentes).

Exemplo: dual de um espaço vetorial de dimensão finita

Cada espaço vetorial de dimensão finita é isomórfico ao seu espaço dual, mas pode haver muitos isomorfismos diferentes entre os dois espaços. Em geral, não há isomorfismo natural entre um espaço vetorial de dimensão finita e seu espaço dual. No entanto, categorias relacionadas (com estrutura adicional e restrições nos mapas) têm um isomorfismo natural, conforme descrito abaixo.

O espaço dual de um espaço vetorial de dimensão finita é novamente um espaço vetorial de dimensão finita da mesma dimensão, e estes são, portanto, isomórficos, uma vez que a dimensão é a única invariante dos espaços vetoriais de dimensão finita sobre um determinado campo. No entanto, na ausência de restrições adicionais (como a exigência de que os mapas preservem a base escolhida), o mapa de um espaço para seu dual não é único e, portanto, tal isomorfismo requer uma escolha e "não é natural". Na categoria de espaços vetoriais de dimensão finita e mapas lineares, pode-se definir um isomorfismo infranatural de espaços vetoriais para seus duais, escolhendo um isomorfismo para cada espaço (digamos, escolhendo uma base para cada espaço vetorial e tomando o isomorfismo correspondente), mas isso não definirá uma transformação natural. Intuitivamente, isso ocorre porque exigiu uma escolha, rigorosamente porque qualquer escolha de isomorfismos não comutará com, digamos, o mapa zero; veja ( Mac Lane & Birkhoff 1999 , § VI.4) para uma discussão detalhada.

Começando com espaços vetoriais de dimensão finita (como objetos) e a identidade e os functores duais, pode-se definir um isomorfismo natural, mas isso requer primeiro a adição de estrutura adicional, em seguida, restringindo os mapas de "todos os mapas lineares" a "mapas lineares que respeitem isso estrutura". Explicitamente, para cada espaço vetorial, exija que ele venha com os dados de um isomorfismo ao seu dual ,. Em outras palavras, tome como objetos espaços vetoriais com uma forma bilinear não degenerada . Isso define um isomorfismo infranatural (isomorfismo para cada objeto). Um em seguida, restringe os mapas para apenas os mapas que comutam com os isomorfismos: ou em outras palavras, preservam a forma bilinear: . (Esses mapas definem o naturalizador dos isomorfismos.) A categoria resultante, com objetos espaços vetoriais de dimensão finita com uma forma bilinear não degenerada, e mapas com transformações lineares que respeitam a forma bilinear, por construção tem um isomorfismo natural da identidade para o dual (cada espaço tem um isomorfismo para seu dual, e os mapas da categoria são obrigados a comutar). Visto sob esta luz, esta construção (adicionar transformações para cada objeto, restringir mapas para comutar com eles) é completamente geral e não depende de nenhuma propriedade particular dos espaços vetoriais. ${\ displaystyle \ eta _ {V} \ dois pontos V \ a V ^ {*}}$ ${\ displaystyle b_ {V} \ dois pontos V \ times V \ a K}$${\ displaystyle T \ dois pontos V \ a U}$${\ displaystyle T ^ {*} (\ eta _ {U} (T (v))) = \ eta _ {V} (v)}$${\ displaystyle b_ {U} (T (v), T (w)) = b_ {V} (v, w)}$

Nesta categoria (espaços vetoriais de dimensão finita com forma bilinear não degenerada, transformadas lineares dos mapas que respeitam a forma bilinear), o dual de um mapa entre espaços vetoriais pode ser identificado como uma transposta . Muitas vezes, por razões de interesse geométrico, isso é especializado em uma subcategoria, exigindo que as formas bilineares não degeneradas tenham propriedades adicionais, como ser simétricas ( matrizes ortogonais ), simétricas e definidas positivas ( espaço do produto interno ), sesquilineares simétricas ( espaços de Hermit ), skew-simétrico e totalmente isotrópico ( espaço vetorial simplético ), etc. - em todas essas categorias um espaço vetorial é naturalmente identificado com seu dual, pela forma bilinear não degenerada.

Operações com transformações naturais

Composição horizontal e vertical de transformações naturais

Se e são transformações naturais entre functores , podemos compô-los para obter uma transformação natural . Isso é feito componente a componente: . ${\ displaystyle \ eta: F \ to G}$${\ displaystyle \ epsilon: G \ a H}$${\ displaystyle F, G, H: C \ a D}$${\ displaystyle \ epsilon \ eta: F \ a H}$${\ displaystyle (\ epsilon \ eta) _ {X} = \ epsilon _ {X} \ eta _ {X}}$

Esta "composição vertical" de transformação natural é associativa e tem uma identidade, e permite que se considere a coleção de todos os próprios functores como uma categoria (veja abaixo em Categorias de Functor ). ${\ displaystyle C \ a D}$

As transformações naturais também têm uma "composição horizontal". Se é uma transformação natural entre functores e é uma transformação natural entre functores , então a composição de functores permite uma composição de transformações naturais onde . ${\ displaystyle \ eta: F \ to G}$${\ displaystyle F, G: C \ a D}$${\ displaystyle \ epsilon: J \ a K}$${\ displaystyle J, K: D \ to E}$${\ displaystyle \ epsilon * \ eta: JF \ to KG}$${\ displaystyle (\ epsilon \ ast \ eta) _ {X} = \ epsilon _ {G (X)} J (\ eta _ {X})}$

Esta operação também é associativa com a identidade, e a identidade coincide com a da composição vertical. As duas operações estão relacionadas por uma identidade que troca composição vertical com composição horizontal: se temos quatro transformações naturais como mostrado na imagem à direita, então a seguinte identidade se mantém ${\ displaystyle \ alpha, \ alpha ', \ beta, \ beta'}$

${\ displaystyle (\ beta '\ alpha') * (\ beta \ alpha) = (\ beta '* \ beta) (\ alpha' * \ alpha).}$

Se é uma transformação natural entre functores , e é outro functor, então podemos formar a transformação natural definindo ${\ displaystyle \ eta: F \ to G}$${\ displaystyle F, G: C \ a D}$${\ displaystyle H: D \ a E}$${\ displaystyle H \ eta: HF \ a HG}$

${\ displaystyle (H \ eta) _ {X} = H (\ eta _ {X}).}$

Se por outro lado é um functor, a transformação natural é definida por ${\ displaystyle K: B \ a C}$${\ displaystyle \ eta K: FK \ to GK}$

${\ displaystyle (\ eta K) _ {X} = \ eta _ {K (X)}.}$

Categorias de funções

Se for qualquer categoria e for uma categoria pequena , podemos formar a categoria de functor tendo como objetos todos os functores de para e como morfismos as transformações naturais entre esses functores. Isso forma uma categoria, pois para qualquer functor há uma transformação natural de identidade (que atribui a cada objeto o morfismo de identidade ) e a composição de duas transformações naturais (a "composição vertical" acima) é novamente uma transformação natural. ${\ displaystyle C}$${\ displaystyle I}$ ${\ displaystyle C ^ {I}}$${\ displaystyle I}$${\ displaystyle C}$${\ displaystyle F}$${\ displaystyle 1_ {F}: F \ a F}$${\ displaystyle X}$${\ displaystyle F (X)}$

Os isomorfismos em são precisamente os isomorfismos naturais. Ou seja, uma transformação natural é um isomorfismo natural se e somente se houver uma transformação natural tal que e . ${\ displaystyle C ^ {I}}$${\ displaystyle \ eta: F \ to G}$${\ displaystyle \ epsilon: G \ a F}$${\ displaystyle \ eta \ epsilon = 1_ {G}}$${\ displaystyle \ epsilon \ eta = 1_ {F}}$

A categoria de functor é especialmente útil se surgir de um gráfico direcionado . Por exemplo, se é a categoria do grafo dirigido • → • , então tem como objetos os morfismos de , e um morfismo entre e em é um par de morfismos e em tal que o "quadrado comuta", ie . ${\ displaystyle C ^ {I}}$${\ displaystyle I}$${\ displaystyle I}$${\ displaystyle C ^ {I}}$${\ displaystyle C}$${\ displaystyle \ phi: U \ to V}$${\ displaystyle \ psi: X \ a Y}$${\ displaystyle C ^ {I}}$${\ displaystyle f: U \ to X}$${\ displaystyle g: V \ to Y}$${\ displaystyle C}$${\ displaystyle \ psi \ circ f = g \ circ \ phi}$

De forma mais geral, pode-se construir a categoria 2, cujo ${\ displaystyle {\ textbf {Cat}}}$

• 0 células (objetos) são as pequenas categorias,
• 1-células (setas) entre dois objetos e são os functores de a ,${\ displaystyle C}$${\ displaystyle D}$${\ displaystyle C}$${\ displaystyle D}$
• 2 células entre duas células 1 (functores) e são as transformações naturais de para .${\ displaystyle F: C \ a D}$${\ displaystyle G: C \ a D}$${\ displaystyle F}$${\ displaystyle G}$

As composições horizontal e vertical são as composições entre as transformações naturais descritas anteriormente. Uma categoria de functor é então simplesmente uma categoria hom nesta categoria (questões de pequenez à parte). ${\ displaystyle C ^ {I}}$

Mais exemplos

Cada limite e colimit fornece um exemplo para uma transformação natural simples, pois um cone equivale a uma transformação natural com o functor diagonal como domínio. De fato, se limites e colimites são definidos diretamente em termos de sua propriedade universal , eles são morfismos universais em uma categoria de functor.

Lema de Yoneda

Se for um objeto de uma pequena categoria localmente , a atribuição define um functor covariante . Este functor é chamado representável (mais geralmente, um functor representável é qualquer functor naturalmente isomorfo a este functor para uma escolha apropriada de ). As transformações naturais de um functor representável para um functor arbitrário são completamente conhecidas e fáceis de descrever; este é o conteúdo do lema de Yoneda . ${\ displaystyle X}$ ${\ displaystyle C}$${\ displaystyle Y \ mapsto {\ text {Hom}} _ {C} (X, Y)}$${\ displaystyle F_ {X}: C \ to {\ textbf {Set}}}$${\ displaystyle X}$${\ displaystyle F: C \ to {\ textbf {Set}}}$

Notas históricas

Diz-se que Saunders Mac Lane , um dos fundadores da teoria das categorias, observou: "Não inventei categorias para estudar functores; eu as inventei para estudar transformações naturais". Assim como o estudo de grupos não está completo sem um estudo de homomorfismos , o estudo de categorias não está completo sem o estudo de functores . A razão para o comentário de Mac Lane é que o estudo dos functores não está completo sem o estudo das transformações naturais.

O contexto da observação de Mac Lane foi a teoria axiomática da homologia . Diferentes maneiras de construir homologia poderiam ser mostradas para coincidir: por exemplo, no caso de um complexo simplicial, os grupos definidos diretamente seriam isomórficos aos da teoria singular. O que não pode ser facilmente expresso sem a linguagem das transformações naturais é como os grupos de homologia são compatíveis com morfismos entre objetos e como duas teorias de homologia equivalentes não apenas têm os mesmos grupos de homologia, mas também os mesmos morfismos entre esses grupos.

Veja também

• Transformação extranatural
• Propriedade universal
• Teoria das categorias superiores

Notas

Referências

links externos

• nLab , um projeto wiki sobre matemática, física e filosofia com ênfase no ponto de vista n- categórico
• André Joyal , CatLab , um projeto wiki dedicado à exposição da matemática categórica
• Hillman, Chris. "A Categorical Primer". CiteSeerX  10.1.1.24.3264 : |url=Introdução formal ausente ou vazia ( ajuda ) à teoria das categorias.
• J. Adamek, H. Herrlich, G. Stecker, Abstract and Concrete Categories-The Joy of Cats
• Stanford Encyclopedia of Philosophy : " Category Theory " - de Jean-Pierre Marquis. Bibliografia extensa.
• Lista de conferências acadêmicas sobre teoria das categorias
• Baez, John, 1996, “ The Tale of n -categories. ” Uma introdução informal às categorias superiores.
• WildCats é um pacote de teoria de categorias para o Mathematica . Manipulação e visualização de objetos, morfismos , categorias, functores , transformações naturais, propriedades universais .
• The catsters , um canal do YouTube sobre teoria das categorias.
• Arquivo de vídeo de palestras gravadas relevantes para categorias, lógica e os fundamentos da física.
• Página da Web interativa que gera exemplos de construções categóricas na categoria de conjuntos finitos.