Espaço vetorial - Vector space
Em matemática , física e engenharia , um espaço vetorial (também chamado de espaço linear ) é um conjunto de objetos chamados vetores , que podem ser somados e multiplicados ("escalados") por números chamados escalares . Os escalares são frequentemente números reais , mas alguns espaços vetoriais têm multiplicação escalar por números complexos ou, geralmente, por um escalar de qualquer campo matemático . As operações de adição vetorial e multiplicação escalar devem satisfazer certos requisitos, chamados axiomas vetoriais (listados abaixo em § Definição ). Para especificar se os escalares em um determinado espaço vetorial são números reais ou complexos, os termos espaço vetorial real e espaço vetorial complexo são freqüentemente usados.
Certos conjuntos de vetores euclidianos são exemplos comuns de um espaço vetorial. Eles representam quantidades físicas como forças , onde quaisquer duas forças do mesmo tipo podem ser adicionadas para produzir uma terceira, e a multiplicação de um vetor de força por um multiplicador real é outro vetor de força. Da mesma forma (mas em um sentido mais geométrico ), vetores que representam deslocamentos no plano ou espaço tridimensional também formam espaços vetoriais. Os vetores em espaços vetoriais não precisam ser necessariamente objetos em forma de flecha, como aparecem nos exemplos mencionados: os vetores são considerados objetos matemáticos abstratos com propriedades particulares, que em alguns casos podem ser visualizados como flechas.
Os espaços vetoriais são o assunto da álgebra linear e são bem caracterizados por sua dimensão , que, grosso modo, especifica o número de direções independentes no espaço. Espaços vetoriais de dimensão infinita surgem naturalmente na análise matemática como espaços de função , cujos vetores são funções . Esses espaços vetoriais são geralmente dotados de alguma estrutura adicional, como uma topologia , que permite a consideração de questões de proximidade e continuidade . Dentre essas topologias, aquelas que são definidas por uma norma ou produto interno são mais comumente utilizadas (equipadas com uma noção de distância entre dois vetores). Este é particularmente o caso dos espaços de Banach e dos espaços de Hilbert , que são fundamentais na análise matemática.
Historicamente, as primeiras ideias que levaram aos espaços vetoriais podem ser rastreadas até a geometria analítica , matrizes , sistemas de equações lineares e vetores euclidianos do século XVII . O tratamento moderno e mais abstrato, formulado pela primeira vez por Giuseppe Peano em 1888, abrange objetos mais gerais do que o espaço euclidiano , mas muito da teoria pode ser vista como uma extensão das idéias geométricas clássicas como linhas , planos e seus análogos de dimensões superiores.
Hoje, os espaços vetoriais são aplicados em matemática , ciências e engenharia . Eles são a noção linear-algébrica apropriada para lidar com sistemas de equações lineares . Eles oferecem uma estrutura para a expansão de Fourier , que é empregada em rotinas de compressão de imagens , e fornecem um ambiente que pode ser usado para técnicas de solução de equações diferenciais parciais . Além disso, os espaços vetoriais fornecem uma maneira abstrata e sem coordenadas de lidar com objetos geométricos e físicos, como tensores . Isso, por sua vez, permite o exame das propriedades locais das variedades por meio de técnicas de linearização. Os espaços vetoriais podem ser generalizados de várias maneiras, levando a noções mais avançadas em geometria e álgebra abstrata .
Este artigo trata principalmente de espaços vetoriais de dimensão finita. No entanto, muitos dos princípios também são válidos para espaços vetoriais de dimensão infinita.
| Estruturas algébricas |
|---|
Introdução e definição
Dois exemplos típicos de espaços vetoriais são descritos primeiro e, em seguida, a definição de espaços vetoriais é introduzida.
Primeiro exemplo: setas no avião
O primeiro exemplo de um espaço vetorial consiste em setas em um plano fixo , começando em um ponto fixo. Isso é usado em física para descrever forças ou velocidades . Dadas quaisquer duas dessas setas, v e w , o paralelogramo medido por essas duas setas contém uma seta diagonal que começa na origem também. Esta nova seta é chamada de soma das duas setas e é denotada por v + w . No caso especial de duas setas na mesma linha, sua soma é a seta dessa linha cujo comprimento é a soma ou a diferença dos comprimentos, dependendo se as setas têm a mesma direção. Outra operação que pode ser feita com setas é escalar: dado qualquer número real positivo a , a seta que tem a mesma direção de v , mas é dilatada ou encolhida pela multiplicação de seu comprimento por a , é chamada de multiplicação de v por a . É denotado um v . Quando a é negativo, um v é definido como a seta apontando na direção oposta.
O seguinte mostra alguns exemplos: se a = 2 , o vetor resultante a w tem a mesma direção de w , mas é esticado até o dobro do comprimento de w (imagem à direita abaixo). Equivalentemente, 2 w é a soma w + w . Além disso, (−1) v = - v tem a direção oposta e o mesmo comprimento de v (vetor azul apontando para baixo na imagem à direita).

|
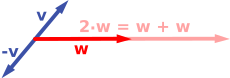
|
Segundo exemplo: pares ordenados de números
Um segundo exemplo chave de um espaço vetorial é fornecido por pares de números reais x e y . (A ordem dos componentes x e y é significativa, assim como um par é também chamado um par ordenado .) Tal como é escrito par ( x , y ) . A soma de dois desses pares e a multiplicação de um par com um número é definida da seguinte forma:
e
O primeiro exemplo acima se reduz a este exemplo, se uma seta for representada por um par de coordenadas cartesianas de seu ponto final.
Definição
Neste artigo, os vetores são representados em negrito para distingui-los dos escalares.
Um espaço vetorial sobre um campo F é um conjunto V junto com duas operações que satisfazem os oito axiomas listados abaixo. A seguir, V × V denota o produto cartesiano de V consigo mesmo, e → denota um mapeamento de um conjunto para outro.
- A primeira operação, a chamada adição de vectores ou simplesmente adição +: V × V → V , leva quaisquer dois vectores de v e w e atribui-lhes um terceiro vector que é vulgarmente escritas como v + w , e chamado a soma desses dois vectores. (O vetor resultante também é um elemento do conjunto V. )
- A segunda operação, chamada multiplicação escalar ·: F × V → V, pega qualquer escalar a e qualquer vetor v e dá outro vetor a v . (Da mesma forma, o vetor a v é um elemento do conjunto V. A multiplicação escalar não deve ser confundida com o produto escalar , também chamado de produto interno ou produto escalar , que é uma estrutura adicional presente em alguns espaços específicos, mas não em todos os vetores . A multiplicação escalar é uma multiplicação de um vetor por um escalar; a outra é uma multiplicação de dois vetores produzindo um escalar.)
Os elementos de V são comumente chamados de vetores . Os elementos de F são comumente chamados de escalares . Símbolos comuns para denotando espaços vector incluem L , V , e W .
Nos dois exemplos acima, o campo é o campo dos números reais, e o conjunto dos vetores consiste nas setas planas com ponto inicial fixo e pares de números reais, respectivamente.
Para se qualificar como um espaço vetorial, o conjunto V e as operações de adição vetorial e multiplicação escalar devem cumprir uma série de requisitos chamados axiomas . Estes estão listados na tabela abaixo, onde u , v e w denotam vectores arbitrárias em V , e um e b denotam escalares em F .
| Axioma | Significado |
|---|---|
| Associatividade da adição de vetores | u + ( v + w ) = ( u + v ) + w |
| Comutatividade da adição de vetor | u + v = v + u |
| Elemento de identidade da adição de vetor | Existe um elemento 0 ∈ V , chamado o vector de zero , de modo a que v + 0 = v para todos v ∈ V . |
| Elementos inversos de adição de vetor | Para todo v ∈ V , existe um elemento - v ∈ V , denominado inverso aditivo de v , tal que v + (- v ) = 0 . |
| Compatibilidade de multiplicação escalar com multiplicação de campo | a ( b v ) = ( ab ) v |
| Elemento de identidade da multiplicação escalar | 1 v = v , onde 1 denota a identidade multiplicativo em F . |
| Distributividade da multiplicação escalar em relação à adição de vetor | a ( u + v ) = a u + a v |
| Distributividade da multiplicação escalar em relação à adição de campo | ( a + b ) v = a v + b v |
Esses axiomas generalizam propriedades dos vetores introduzidos nos exemplos acima. Na verdade, o resultado da adição de dois pares ordenados (como no segundo exemplo acima) não depende da ordem das somas:
- ( x v , y v ) + ( x w , y w ) = ( x w , y w ) + ( x v , y v ) .
Da mesma forma, no exemplo geométrico de vetores como setas, v + w = w + v uma vez que o paralelogramo que define a soma dos vetores é independente da ordem dos vetores. Todos os outros axiomas podem ser verificados de maneira semelhante em ambos os exemplos. Assim, ao desconsiderar a natureza concreta do tipo particular de vetores, a definição incorpora esses dois e muitos mais exemplos em uma noção de espaço vetorial.
A subtração de dois vetores e divisão por um escalar (diferente de zero) pode ser definida como
Quando o campo escalar F são os números reais R , o espaço vetorial é chamado de espaço vetorial real . Quando o campo escalar são os números complexos C , o espaço vetorial é chamado de espaço vetorial complexo . Esses dois casos são os mais usados na engenharia. A definição geral de um espaço vector permite escalares para ser elementos de qualquer fixo campo F . A noção é então conhecida como um F - espaço vectorial ou um espaço vectorial mais de F . Um campo é, essencialmente, um conjunto de números que possui operações de adição , subtração , multiplicação e divisão . Por exemplo, números racionais formam um campo.
Em contraste com a intuição proveniente de vetores no plano e casos de dimensões superiores, em espaços vetoriais em geral, não há noção de proximidade , ângulos ou distâncias . Para lidar com essas questões, tipos específicos de espaços vetoriais são introduzidos; veja § Espaços vetoriais com estrutura adicional abaixo para mais.
Formulações alternativas e consequências elementares
Além vector e multiplicação escalar são operações, satisfazendo o fecho propriedade: u + v e uma v são em V para todos um em F , e u , v em V . Algumas fontes mais antigas mencionam essas propriedades como axiomas separados.
No jargão da álgebra abstrata , os primeiros quatro axiomas são equivalentes a exigir que o conjunto de vetores seja um grupo abeliano sob adição. Os restantes axiomas dar a este grupo um F - módulo de estrutura. Em outras palavras, existe um homomorfismo de anel f do campo F para o anel de endomorfismo do grupo de vetores. Então a multiplicação escalar a v é definida como ( f ( a )) ( v ) .
Existem várias consequências diretas dos axiomas do espaço vetorial. Alguns deles derivam da teoria elementar de grupos , aplicada ao grupo aditivo de vetores: por exemplo, o vetor zero 0 de V e o inverso aditivo - v de qualquer vetor v são únicos. Outras propriedades seguem empregando também a lei distributiva para a multiplicação escalar, por exemplo a v é igual a 0 se e somente se a é igual a 0 ou v é igual a 0 .
História
Os espaços vetoriais derivam da geometria afim , por meio da introdução de coordenadas no plano ou espaço tridimensional. Por volta de 1636, os matemáticos franceses René Descartes e Pierre de Fermat fundaram a geometria analítica identificando soluções para uma equação de duas variáveis com pontos em uma curva plana . Para conseguir soluções geométricas sem o uso de coordenadas, Bolzano introduziu, em 1804, certas operações sobre pontos, retas e planos, que são antecessores dos vetores. Möbius (1827) introduziu a noção de coordenadas baricêntricas . Bellavitis (1833) introduziu a noção de biponto, ou seja, um segmento orientado cuja extremidade é a origem e a outra o alvo. Os vetores foram reconsiderados com a apresentação de números complexos por Argand e Hamilton e o início dos quatérnios por este último. Eles são elementos em R 2 e R 4 ; tratá-los usando combinações lineares remonta a Laguerre em 1867, que também definiu sistemas de equações lineares .
Em 1857, Cayley introduziu a notação de matriz que permite uma harmonização e simplificação de mapas lineares . Na mesma época, Grassmann estudou o cálculo baricêntrico iniciado por Möbius. Ele imaginou conjuntos de objetos abstratos dotados de operações. Em sua obra, os conceitos de independência linear e dimensão , bem como produtos escalares estão presentes. Na verdade, a obra de Grassmann de 1844 ultrapassa o quadro dos espaços vetoriais, pois também a sua multiplicação ponderada o conduziu ao que hoje se chama de álgebras . O matemático italiano Peano foi o primeiro a dar a definição moderna de espaços vetoriais e mapas lineares em 1888.
Um importante desenvolvimento dos espaços vetoriais se deve à construção de espaços funcionais por Henri Lebesgue . Isso foi formalizado posteriormente por Banach e Hilbert , por volta de 1920. Naquela época, a álgebra e o novo campo da análise funcional começaram a interagir, notadamente com conceitos-chave como espaços de funções p- integráveis e espaços de Hilbert . Também nessa época, foram feitos os primeiros estudos sobre espaços vetoriais de dimensão infinita.
Exemplos
Coordenar espaço
O exemplo mais simples de um espaço vetorial sobre um campo F é o próprio campo F (visto que é um grupo abeliano para adição, uma parte dos requisitos para ser um campo .), Equipado com sua adição (torna-se adição vetorial.) E multiplicação (Torna-se multiplicação escalar.). Mais geralmente, todas as n- duplas (sequências de comprimento n )
- ( a 1 , a 2 , ..., a n )
dos elementos a i de F formam um espaço vetorial que geralmente é denotado por F n e chamado de espaço de coordenadas . O caso n = 1 é o exemplo mais simples mencionado acima, no qual o campo F também é considerado um espaço vetorial sobre si mesmo. O caso M = R e n = 2 (modo de R 2 ) foi discutido na introdução acima.
Números complexos e outras extensões de campo
O conjunto de números complexos C , isto é, números que podem ser escritas na forma x + iy para números reais x e y , onde i é a unidade imaginária , formam um espaço vectorial sobre os reais com a adição habitual e multiplicação: ( x + iy ) + ( a + ib ) = ( x + a ) + i ( y + b ) e c ⋅ ( x + iy ) = ( c ⋅ x ) + i ( c ⋅ y ) para números reais x , y , um , b e c . Os vários axiomas de um espaço vetorial decorrem do fato de que as mesmas regras são válidas para a aritmética de números complexos.
Na verdade, o exemplo de números complexos é essencialmente o mesmo que (isto é, é isomórfico a) o espaço vetorial de pares ordenados de números reais mencionados acima: se pensarmos no número complexo x + i y como representando o par ordenado ( x , y ) no plano complexo então vemos que as regras para adição e multiplicação escalar correspondem exatamente àquelas no exemplo anterior.
Mais geralmente, as extensões de campo proporcionam uma outra classe de exemplos de espaço vectorial, em particular em álgebra e teoria número algébrica : um campo F que contém um campo menor E é um E espaço -vector, por os dados de operações de multiplicação e adição de F . Por exemplo, os números complexos são um espaço vectorial mais de R , e a extensão do campo é um espaço vectorial sobre Q .
Espaços funcionais
Funções de qualquer conjunto fixo Ω para um campo F também formam espaços vetoriais, realizando adição e multiplicação escalar pontualmente. Isto é, a soma das duas funções f e g é a função ( f + g ) dado pela
- ( f + g ) ( w ) = f ( w ) + g ( w ) ,
e da mesma forma para multiplicação. Tais espaços de funções ocorrer em muitas situações geométricas, quando Ω é a reta real ou um intervalo , ou outros subconjuntos de R . Muitas noções em topologia e análise, como continuidade , integrabilidade ou diferenciabilidade são bem comportadas com respeito à linearidade: somas e múltiplos escalares de funções que possuem tal propriedade ainda possuem essa propriedade. Portanto, o conjunto de tais funções são espaços vetoriais. Eles são estudados em maior detalhe usando os métodos de análise funcional , veja abaixo . As restrições algébricas também produzem espaços vetoriais: o espaço vetorial F [x] é dado por funções polinomiais :
- f ( x ) = R 0 + r 1 x + ... + r n -1 x n -1 + r n x n , onde os coeficientes de r 0 , ..., r n são em F .
Equações lineares
Os sistemas de equações lineares homogêneas estão intimamente ligados aos espaços vetoriais. Por exemplo, as soluções de
uma + 3 b + c = 0 4 a + 2 b + 2 c = 0
são dados por triplos com a , b = a / 2 e c = −5 a / 2 arbitrários . Eles formam um espaço vetorial: somas e múltiplos escalares de tais triplos ainda satisfazem as mesmas razões das três variáveis; portanto, também são soluções. As matrizes podem ser usadas para condensar várias equações lineares como acima em uma equação vetorial, a saber
- A x = 0 ,
onde é a matriz que contém os coeficientes das equações dadas, x é o vetor ( a , b , c ) , A x denota o produto da matriz e 0 = (0, 0) é o vetor zero. De maneira semelhante, as soluções de equações diferenciais lineares homogêneas formam espaços vetoriais. Por exemplo,
- f ′ ′ ( x ) + 2 f ′ ( x ) + f ( x ) = 0
retorna f ( x ) = a e - x + bx e - x , onde a e b são constantes arbitrárias e e x é a função exponencial natural .
Base e dimensão

As bases permitem representar vetores por uma sequência de escalares chamados de coordenadas ou componentes . Uma base é um conjunto B = { b i } i ∈ I de vetores b i , por conveniência, muitas vezes indexado por algum conjunto de índice I , que abrange todo o espaço e é linearmente independente . "Abrangendo todo o espaço" significa que qualquer vetor v pode ser expresso como uma soma finita (chamada de combinação linear ) dos elementos de base:
-
( 1 )
onde o um k são escalares, chamados as coordenadas (ou componentes) do vector v , com respeito à base B , e b i k ( k = 1, ..., n ) elementos de B . Independência linear significa que as coordenadas a k são exclusivamente determinadas para qualquer vetor no espaço vetorial.
Por exemplo, os vetores de coordenadas e 1 = (1, 0, ..., 0) , e 2 = (0, 1, 0, ..., 0) , a e n = (0, 0, ..., 0, 1) , formam uma base de F n , chamada de base padrão , uma vez que qualquer vetor ( x 1 , x 2 , ..., x n ) pode ser expresso exclusivamente como uma combinação linear desses vetores:
- ( x 1 , x 2 ,…, x n ) = x 1 (1, 0,…, 0) + x 2 (0, 1, 0,…, 0) + ⋯ + x n (0,…, 0, 1) = x 1 e 1 + x 2 e 2 + ⋯ + x n e n .
As coordenadas correspondentes x 1 , x 2 , … , x n são apenas as coordenadas cartesianas do vetor.
Todo espaço vetorial tem uma base. Isso segue do lema de Zorn , uma formulação equivalente do Axioma da Escolha . Dados os outros axiomas da teoria dos conjuntos de Zermelo – Fraenkel , a existência de bases é equivalente ao axioma da escolha. O lema do ultrafiltro , que é mais fraco do que o axioma de escolha, implica que todas as bases de um determinado espaço vetorial têm o mesmo número de elementos, ou cardinalidade (cf. teorema da dimensão para espaços vetoriais ). É chamada a dimensão do espaço vectorial, denotada por dim V . Se o espaço é medido por um número finito de vetores, as afirmações acima podem ser provadas sem essa entrada fundamental da teoria dos conjuntos.
A dimensão do espaço de coordenadas F n é n , pela base exibida acima. A dimensão do anel polinomial F [ x ] introduzido acima é contavelmente infinito , uma base é dada por 1 , x , x 2 , ... A fortiori , a dimensão de espaços de funções mais gerais, como o espaço de funções em alguns (limitados ou ilimitado) intervalo, é infinito. Sob suposições de regularidade adequadas sobre os coeficientes envolvidos, a dimensão do espaço de solução de uma equação diferencial ordinária homogênea é igual ao grau da equação. Por exemplo, o espaço de solução para a equação acima é gerado por e - x e xe - x . Essas duas funções são linearmente independentes sobre R , então a dimensão desse espaço é dois, assim como o grau da equação.
Uma extensão de campo sobre os racionais Q pode ser pensada como um espaço vetorial sobre Q (definindo adição de vetor como adição de campo, definição de multiplicação escalar como multiplicação de campo por elementos de Q e, de outra forma, ignorando a multiplicação de campo). A dimensão (ou grau ) da extensão do campo Q ( α ) sobre Q depende de α . Se α satisfaz alguma equação polinomial
Mapas e matrizes lineares
A relação de dois espaços vetoriais pode ser expressa por mapa linear ou transformação linear . São funções que refletem a estrutura do espaço vetorial, ou seja, preservam somas e multiplicação escalar:
- e f ( um · v ) = um · F ( v ) para todos v e w em V , tudo um em F .
Um isomorfismo é um mapa linear f : V → W de tal modo que existe um mapa inverso g : W → V , que é um mapa de tal modo que as duas possíveis composições f ∘ g : W → W e g ∘ f : V → V são mapas de identidade . Equivalentemente, f é tanto um para um ( injetivo ) quanto on ( sobrejetivo ). Se existe um isomorfismo entre V e W , os dois espaços são ditos isomórficos ; eles são, então, essencialmente idênticos como espaços vetoriais, uma vez que todas as identidades contidas em V são, via f , transportadas para outras semelhantes em W , e vice-versa via g .
Por exemplo, os espaços vetoriais "setas no plano" e "pares ordenados de números" na introdução são isomórficos: uma seta planar v partindo da origem de algum sistema de coordenadas (fixo) pode ser expressa como um par ordenado, considerando o x - ey - componente da seta, conforme mostrado na imagem à direita. Inversamente, dado um par ( x , y ) , a seta que passa por x para a direita (ou para a esquerda, se x for negativo) ey para cima (para baixo, se y for negativo) volta a seta v .
Mapas lineares V → W entre dois espaços vetoriais formam um espaço vetorial Hom F ( V , W ) , também denotado L ( V , W ) , ou 𝓛 ( V , W ) . O espaço dos mapas lineares de V a F é chamado de espaço vetorial dual , denotado por V ∗ . Por meio do mapa natural injetivo V → V ∗∗ , qualquer espaço vetorial pode ser embutido em seu bidual ; o mapa é um isomorfismo se e somente se o espaço for de dimensão finita.
Uma vez que uma base de V é escolhida, os mapas lineares f : V → W são completamente determinados pela especificação das imagens dos vetores de base, porque qualquer elemento de V é expresso exclusivamente como uma combinação linear deles. Se dim V = dim W , uma correspondência 1-para-um entre as bases fixas de V e W dá origem a um mapa linear que mapeia qualquer elemento base de V para o elemento de base correspondente de W . É um isomorfismo, por sua própria definição. Portanto, dois espaços vetoriais são isomórficos se suas dimensões concordarem e vice-versa. Outra forma de expressar isso é que qualquer espaço vetorial é completamente classificado ( até o isomorfismo) por sua dimensão, um único número. Em particular, qualquer espaço vetorial F n- dimensional V é isomórfico a F n . Não há, entretanto, nenhum isomorfismo "canônico" ou preferencial; na verdade, um isomorfismo φ : F n → V é equivalente à escolha de uma base de V , mapeando a base padrão de F n para V , via φ . A liberdade de escolher uma base conveniente é particularmente útil no contexto de dimensão infinita; veja abaixo .
Matrizes
Matrizes são uma noção útil para codificar mapas lineares. Eles são escritos como uma matriz retangular de escalares, como na imagem à direita. Qualquer matriz A m -by- n dá origem a um mapa linear de F n a F m , pelo seguinte
- , onde denota soma ,
ou, usando a multiplicação da matriz A com o vetor de coordenadas x :
- x ↦ A x .
Além disso, após escolher as bases de V e W , qualquer mapa linear f : V → W é representado exclusivamente por uma matriz por meio desta atribuição.
O determinante det ( A ) de uma matriz quadrada A é um escalar que informa se o mapa associado é um isomorfismo ou não: para ser assim, é suficiente e necessário que o determinante seja diferente de zero. A transformação linear de R n correspondente a uma matriz real n -by- n preserva a orientação se e somente se seu determinante for positivo.
Autovalores e autovetores
Endomorfismos , mapas lineares f : V → V , são particularmente importantes uma vez que, neste caso, os vetores v podem ser comparados com sua imagem sob f , f ( v ) . Qualquer vetor diferente de zero v satisfazendo λ v = f ( v ) , onde λ é um escalar, é chamado de autovetor de f com autovalor λ . Equivalentemente, v é um elemento do núcleo da diferença f - λ · Id (onde Id é o mapa de identidade V → V ) . Se V for finito-dimensional, isso pode ser reformulado usando determinantes: f tendo autovalor λ é equivalente a
- det ( f - λ · Id) = 0 .
Ao explicitar a definição do determinante, a expressão do lado esquerdo pode ser vista como uma função polinomial em λ , chamada de polinômio característico de f . Se o campo F for grande o suficiente para conter um zero desse polinômio (o que ocorre automaticamente para F algebricamente fechado , como F = C ), qualquer mapa linear tem pelo menos um autovetor. O espaço vetorial V pode ou não possuir uma base própria , uma base que consiste em vetores próprios. Este fenômeno é governado pela forma canônica do mapa de Jordan . O conjunto de todos os vectores eigen que correspondem a um valor próprio particular de f forma um espaço vector conhecido como o auto-espaço correspondente para o valor próprio (e f ) em questão. Para alcançar o teorema espectral , a afirmação correspondente no caso de dimensão infinita, a maquinaria da análise funcional é necessária, veja abaixo .
Construções básicas
Além dos exemplos concretos acima, há uma série de construções algébricas lineares padrão que geram espaços vetoriais relacionados a alguns. Além das definições fornecidas a seguir, eles também são caracterizados por propriedades universais , que determinam um objeto X especificando os mapas lineares de X para qualquer outro espaço vetorial.
Subespaços e espaços quocientes
Um subconjunto não vazio W de um espaço vetorial V que é fechado sob adição e multiplicação escalar (e, portanto, contém o vetor 0 de V ) é chamado de subespaço linear de V , ou simplesmente um subespaço de V , quando o espaço ambiente é inequivocamente um Espaço vetorial. Subespaços de V são espaços vetoriais (sobre o mesmo campo) em seu próprio direito. A intersecção de todos os subespaços contendo um dado conjunto S de vectores é chamado a sua extensão , e é menor o subespaço de V que contém o conjunto S . Expresso em termos de elementos, o intervalo é o subespaço que consiste de todas as combinações lineares de elementos de S .
Um subespaço linear de dimensão 1 é uma linha vetorial . Um subespaço linear de dimensão 2 é um plano vetorial . Um subespaço linear que contém todos os elementos, exceto um de uma base do espaço ambiente, é um hiperplano vetorial . Em um espaço vetorial de dimensão finita n , um hiperplano vetorial é, portanto, um subespaço de dimensão n - 1 .
A contraparte dos subespaços são espaços vetoriais quocientes . Dado qualquer subespaço W ⊂ V , o espaço quociente V / W (" V módulo W ") é definido da seguinte forma: como um conjunto, consiste em v + W = { v + w : w ∈ W }, onde v é um vetor arbitrário em V . A soma de dois de tais elementos de v 1 + W e v 2 + W é ( v 1 + v 2 ) + W , e multiplicação escalar é dada por um · ( v + W ) = ( um · v ) + W . O ponto chave desta definição é que v 1 + W = v 2 + W se e apenas se a diferença de v 1 e v 2 encontra-se em W . Desta forma, o espaço quociente "esquece" a informação que está contida no subespaço W .
O núcleo ker ( f ) de um mapa linear f : V → W é composto por vectores de v que são mapeados para 0 em W . O kernel e a imagem im ( f ) = { f ( v ): v ∈ V } são subespaços de V e W , respectivamente. A existência de núcleos e imagens faz parte da afirmação de que a categoria de espaços vetoriais (sobre um campo fixo F ) é uma categoria abeliana , ou seja, um corpus de objetos matemáticos e mapas preservadores de estrutura entre eles (uma categoria ) que se comporta muito parecido com a categoria de grupos abelianos . Por causa disso, muitas declarações, como o primeiro teorema do isomorfismo (também chamado de teorema da nulidade de classificação em termos relacionados à matriz)
- V / ker ( f ) ≡ im ( f ).
e o segundo e terceiro teorema do isomorfismo podem ser formulados e provados de uma maneira muito semelhante às declarações correspondentes para grupos .
Um exemplo importante é o kernel de uma aplicação linear x ↦ A x para alguma matriz fixa A , como acima . O núcleo deste mapa é o subespaço de vectores x , tais que A x = 0 , o que é precisamente o conjunto de soluções para o sistema de equações lineares homogéneos pertencentes a um . Este conceito também se estende a equações diferenciais lineares
- , onde os coeficientes a i também são funções em x .
No mapa correspondente
- ,
as derivadas da função f aparecem linearmente (em oposição a f ′ ′ ( x ) 2 , por exemplo). Como a diferenciação é um procedimento linear (ou seja, ( f + g ) ′ = f ′ + g ′ e ( c · f ) ′ = c · f ′ para uma constante c ), essa atribuição é linear, chamada de operador diferencial linear . Em particular, as soluções para a equação diferencial D ( f ) = 0 formam um espaço vetorial (sobre R ou C ).
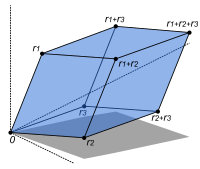
Produto direto e soma direta
O produto direto dos espaços vetoriais e a soma direta dos espaços vetoriais são duas maneiras de combinar uma família indexada de espaços vetoriais em um novo espaço vetorial.
O produto direto de uma família de espaços vetoriais V i consiste no conjunto de todas as tuplas ( v i ) i ∈ I , que especificam para cada índice i em algum conjunto de índices I um elemento v i de V i . A adição e a multiplicação escalar são executadas componente a componente. Uma variante dessa construção é a soma direta (também chamada de coproduto e denotada ), onde apenas tuplas com um número finito de vetores diferentes de zero são permitidas. Se o conjunto de índices I for finito, as duas construções concordam, mas em geral são diferentes.
Produto tensor
O produto tensorial V ⊗ F W , ou simplesmente V ⊗ W , de dois espaços vetoriais V e W é uma das noções centrais da álgebra multilinear que trata da extensão de noções como mapas lineares para várias variáveis. Um mapa g : V × W → X é denominado bilinear se g for linear em ambas as variáveis v e w . Ou seja, para w fixo, a aplicação v ↦ g ( v , w ) é linear no sentido acima e da mesma forma para v fixo .
O produto tensorial é um espaço vetorial particular que é um recipiente universal de mapas bilineares g , como segue. É definido como o espaço vetorial que consiste em somas finitas (formais) de símbolos chamados tensores
- v 1 ⊗ w 1 + v 2 ⊗ w 2 + ⋯ + v n ⊗ w n ,
sujeito às regras
- a · ( v ⊗ w ) = ( a · v ) ⊗ w = v ⊗ ( a · w ), onde a é um escalar,
- ( v 1 + v 2 ) ⊗ w = v 1 ⊗ w + v 2 ⊗ w , e
- v ⊗ ( w 1 + w 2 ) = v ⊗ w 1 + v ⊗ w 2 .

Essas regras garantem que o mapa f de V × W para V ⊗ W que mapeia uma tupla ( v , w ) para v ⊗ w seja bilinear. A universalidade afirma que dado qualquer espaço vetorial X e qualquer mapa bilinear g : V × W → X , existe um único mapa u , mostrado no diagrama com uma seta pontilhada, cuja composição com f é igual a g : u ( v ⊗ w ) = g ( v , w ) . Isso é chamado de propriedade universal do produto tensorial, uma instância do método - muito usado na álgebra abstrata avançada - para definir indiretamente objetos especificando mapas de ou para esse objeto.
Espaços vetoriais com estrutura adicional
Do ponto de vista da álgebra linear, os espaços vetoriais são completamente compreendidos na medida em que qualquer espaço vetorial se caracteriza, até o isomorfismo, por sua dimensão. No entanto, os espaços vetoriais em si não oferecem uma estrutura para lidar com a questão - crucial para a análise - se uma sequência de funções converge para outra função. Da mesma forma, a álgebra linear não é adaptada para lidar com séries infinitas , uma vez que a operação de adição permite que apenas termos finitos sejam adicionados. Portanto, as necessidades de análise funcional requerem a consideração de estruturas adicionais.
Um espaço vetorial pode receber uma ordem parcial ≤, sob a qual alguns vetores podem ser comparados. Por exemplo, o espaço real n- dimensional R n pode ser ordenado comparando seus vetores componente a componente. Espaços vetoriais ordenados , por exemplo , espaços de Riesz , são fundamentais para a integração de Lebesgue , que depende da capacidade de expressar uma função como uma diferença de duas funções positivas
- ,
onde denota a parte positiva e a parte negativa.
Espaços vetoriais normados e espaços internos de produto
A "medição" de vetores é feita especificando-se uma norma , um datum que mede o comprimento dos vetores, ou por um produto interno , que mede os ângulos entre os vetores. Normas e produtos internos são denotados e , respectivamente. O datum de um produto interno implica que comprimentos de vetores também podem ser definidos, definindo a norma associada . Os espaços vetoriais dotados de tais dados são conhecidos como espaços vetoriais normados e espaços de produto interno , respectivamente.
O espaço de coordenadas F n pode ser equipado com o produto escalar padrão :
Em R 2 , isso reflete a noção comum do ângulo entre dois vetores x e y , pela lei dos cossenos :
Por causa disso, dois vetores que satisfazem são chamados ortogonais . Uma variante importante do produto escalar padrão é usada no espaço de Minkowski : R 4 dotado com o produto Lorentz
Em contraste com o produto escalar padrão, não é definido positivo : também aceita valores negativos, por exemplo, para . Escolher a quarta coordenada - correspondente ao tempo , em oposição a três dimensões espaciais - torna-a útil para o tratamento matemático da relatividade especial .
Espaços vetoriais topológicos
As questões de convergência são tratadas considerando os espaços vetoriais V que possuem uma topologia compatível , uma estrutura que permite falar sobre a proximidade dos elementos . Compatível aqui significa que adição e multiplicação escalar devem ser mapas contínuos . Grosso modo, se x e y em V e a em F variam por um valor limitado, o mesmo ocorre com x + y e a x . Para fazer sentido na especificação de quanto um escalar muda, o campo F também precisa carregar uma topologia neste contexto; uma escolha comum são os reais ou os números complexos.
Em tais espaços vetoriais topológicos, pode-se considerar uma série de vetores. A soma infinita
indica o limite dos correspondentes somas parciais finitas da sequência ( f i ) i ∈ N de elementos de V . Por exemplo, o f i podem ser funções (reais ou complexas) pertencentes a algum espaço de função V , caso em que a série é uma série de funções . O modo de convergência das séries depende da topologia imposta ao espaço de funções. Em tais casos, a convergência pontual e a convergência uniforme são dois exemplos proeminentes.

Uma forma de garantir a existência de limites de certas séries infinitas é restringir a atenção aos espaços onde qualquer sequência de Cauchy tem um limite; esse espaço vetorial é denominado completo . A grosso modo, um espaço vetorial está completo desde que contenha todos os limites necessários. Por exemplo, o espaço vetorial de polinômios no intervalo unitário [0,1], equipado com a topologia de convergência uniforme não é completo porque qualquer função contínua em [0,1] pode ser uniformemente aproximada por uma sequência de polinômios, pelo Teorema da aproximação de Weierstrass . Em contraste, o espaço de todas as funções contínuas em [0,1] com a mesma topologia está completo. Uma norma dá origem a uma topologia ao definir que uma sequência de vetores v n converge para v se e somente se
Os espaços de Banach e Hilbert são espaços vetoriais topológicos completos cujas topologias são dadas, respectivamente, por uma norma e um produto interno. Seu estudo - uma peça-chave da análise funcional - concentra-se em espaços vetoriais de dimensão infinita, uma vez que todas as normas em espaços vetoriais topológicos de dimensão finita dão origem à mesma noção de convergência. A imagem à direita mostra a equivalência da norma 1 e da norma ∞ em R 2 : como as "bolas" de unidade se encerram, uma sequência converge para zero em uma norma se e somente se o fizer na outra norma . No caso de dimensão infinita, entretanto, geralmente haverá topologias inequivalentes, o que torna o estudo de espaços vetoriais topológicos mais rico do que o de espaços vetoriais sem dados adicionais.
Do ponto de vista conceitual, todas as noções relacionadas a espaços vetoriais topológicos devem corresponder à topologia. Por exemplo, em vez de considerar todos os mapas lineares (também chamados de funcionais ) V → W , os mapas entre espaços vetoriais topológicos devem ser contínuos. Em particular, o espaço dual (topológico) V ∗ consiste em funcionais contínuos V → R (ou para C ). O teorema Hahn-Banach fundamental está preocupado com a separação de subespaços de espaços vetoriais topológicos apropriados por funcionais contínuos.
Espaços Banach
Os espaços de Banach , introduzidos por Stefan Banach , são espaços vetoriais normatizados completos.
Um primeiro exemplo é o espaço vetorial que consiste em vetores infinitos com entradas reais cuja norma dada por
- para e .
As topologias no espaço de dimensão infinita são diferentes para diferentes . Por exemplo, a sequência de vetores , em que estão os primeiros componentes e os seguintes , converge para o vetor zero para , mas não para :
- , mas
Mais geralmente do que as sequências de números reais, as funções são dotadas de uma norma que substitui a soma acima pela integral de Lebesgue
Os espaços de funções integráveis em um determinado domínio (por exemplo, um intervalo) satisfatórios , e equipados com esta norma, são denominados espaços de Lebesgue , denotados .
Esses espaços estão completos. (Se usarmos a integral de Riemann em vez disso, o espaço não estará completo, o que pode ser visto como uma justificativa para a teoria da integração de Lebesgue.) Concretamente, isso significa que para qualquer sequência de funções integráveis de Lebesgue com , satisfazendo a condição
existe uma função pertencente ao espaço vetorial tal que
A imposição de condições de limite não apenas na função, mas também em suas derivadas leva a espaços de Sobolev .
Espaços de Hilbert
Os espaços de produtos internos completos são conhecidos como espaços de Hilbert , em homenagem a David Hilbert . O espaço de Hilbert L 2 (Ω), com o produto interno dado por
onde denota o conjugado complexo de g ( x ), é um caso chave.
Por definição, em um espaço de Hilbert, qualquer sequência de Cauchy converge para um limite. Por outro lado, encontrar uma sequência de funções f n com propriedades desejáveis que se aproximam de uma determinada função limite é igualmente crucial. A análise inicial, sob o pretexto da aproximação de Taylor , estabeleceu uma aproximação de funções diferenciáveis f por polinômios. Pelo teorema de Stone-Weierstrass , cada função contínua em [ a , b ] pode ser aproximada tão perto quanto desejado por um polinômio. Uma técnica de aproximação semelhante por funções trigonométricas é comumente chamada de expansão de Fourier e é muito aplicada em engenharia, veja abaixo . De forma mais geral e mais conceitual, o teorema produz uma descrição simples de quais "funções básicas", ou, em espaços de Hilbert abstratos, quais vetores básicos são suficientes para gerar um espaço de Hilbert H , no sentido de que o fechamento de seu período (isto é , combinações lineares finitas e limites daqueles) é todo o espaço. Esse conjunto de funções é denominado base de H , sua cardinalidade é conhecida como dimensão espacial de Hilbert . O teorema não apenas exibe funções de base adequadas como suficientes para fins de aproximação, mas também, juntamente com o processo de Gram-Schmidt , permite construir uma base de vetores ortogonais . Essas bases ortogonais são a generalização do espaço de Hilbert dos eixos coordenados no espaço euclidiano de dimensão finita .
As soluções para várias equações diferenciais podem ser interpretadas em termos de espaços de Hilbert. Por exemplo, muitos campos da física e da engenharia levam a tais equações e frequentemente soluções com propriedades físicas particulares são usadas como funções básicas, muitas vezes ortogonais. Como um exemplo da física, a equação de Schrödinger dependente do tempo na mecânica quântica descreve a mudança das propriedades físicas no tempo por meio de uma equação diferencial parcial , cujas soluções são chamadas de funções de onda . Valores definidos para propriedades físicas, como energia ou momentum, correspondem aos autovalores de um determinado operador diferencial (linear) e as funções de onda associadas são chamadas de autoestados . O teorema espectral decompõe um operador linear compacto agindo sobre funções em termos dessas autofunções e seus autovalores.
Álgebras sobre campos

Espaços vetoriais gerais não possuem multiplicação entre vetores. Um espaço vetorial equipado com um operador bilinear adicional que define a multiplicação de dois vetores é uma álgebra sobre um campo . Muitas álgebras derivam de funções em algum objeto geométrico: uma vez que funções com valores em um determinado campo podem ser multiplicadas pontualmente, essas entidades formam álgebras. O teorema de Stone-Weierstrass, por exemplo, se baseia em álgebras de Banach que são espaços e álgebras de Banach.
A álgebra comutativa faz grande uso de anéis de polinômios em uma ou várias variáveis, apresentadas acima . Sua multiplicação é comutativa e associativa . Esses anéis e seus quocientes formam a base da geometria algébrica , porque são anéis de funções de objetos geométricos algébricos .
Outro exemplo crucial são as álgebras de Lie , que não são nem comutativas nem associativas, mas o não-fato é limitado pelas restrições ( [ x , y ] denota o produto de x e y ):
- [ x , y ] = - [ y , x ] ( anticomutatividade ), e
- [ x , [ y , z ]] + [ y , [ z , x ]] + [ z , [ x , y ]] = 0 ( identidade de Jacobi ).
Exemplos incluem o espaço vectorial de n -by- n matrizes, com [ x , y ] = xy - yx , o comutador de duas matrizes, e R 3 , dotado com o produto cruzado .
A álgebra tensorial T ( V ) é uma maneira formal de adicionar produtos a qualquer espaço vetorial V para obter uma álgebra. Como um espaço vetorial, é dividido por símbolos, chamados de tensores simples
- v 1 ⊗ v 2 ⊗ ⋯ ⊗ v n , onde o grau n varia.
A multiplicação é dada pela concatenação de tais símbolos, impondo a lei distributiva sob adição e exigindo que a multiplicação escalar comute com o produto tensorial ⊗, da mesma forma que com o produto tensorial de dois espaços vetoriais introduzidos acima . De um modo geral, não há nenhuma relação entre v 1 ⊗ v 2 e v 2 ⊗ v 1 . Forçar dois desses elementos a serem iguais leva à álgebra simétrica , ao passo que forçar v 1 ⊗ v 2 = - v 2 ⊗ v 1 resulta na álgebra externa .
Quando um campo, F é declarado explicitamente, um termo comum usado é F- álgebra.
Formulários
Os espaços vetoriais têm muitas aplicações, pois ocorrem com frequência em circunstâncias comuns, nomeadamente onde funções com valores em algum campo estão envolvidas. Eles fornecem uma estrutura para lidar com problemas analíticos e geométricos ou são usados na transformada de Fourier. Esta lista não é exaustiva: existem muitos outros aplicativos, por exemplo, em otimização . O teorema minimax da teoria dos jogos, que afirma a existência de um pagamento único quando todos os jogadores jogam de forma otimizada, pode ser formulado e comprovado usando métodos de espaços vetoriais. A teoria da representação transfere proveitosamente o bom entendimento da álgebra linear e dos espaços vetoriais para outros domínios matemáticos, como a teoria dos grupos .
Distribuições
Uma distribuição (ou função generalizada ) é um mapa linear que atribui um número a cada função de "teste" , normalmente uma função suave com suporte compacto , de forma contínua: na terminologia acima, o espaço de distribuições é o dual (contínuo) do espaço de função de teste. Este último espaço é dotado de uma topologia que leva em consideração não apenas o próprio f , mas também todas as suas derivadas superiores. Um exemplo padrão é o resultado da integração de uma função de teste f em algum domínio Ω:
Quando Ω = { p } , conjunto constituído por um único ponto, este se reduz à distribuição de Dirac , denotada por δ , que associa a uma função teste f seu valor em p : δ ( f ) = f ( p ) . As distribuições são um instrumento poderoso para resolver equações diferenciais. Uma vez que todas as noções analíticas padrão, como derivadas, são lineares, elas se estendem naturalmente ao espaço das distribuições. Portanto, a equação em questão pode ser transferida para um espaço de distribuição, que é maior do que o espaço da função subjacente, de modo que métodos mais flexíveis estão disponíveis para resolver a equação. Por exemplo, as funções e soluções fundamentais de Green são geralmente distribuições em vez de funções adequadas e podem ser usadas para encontrar soluções da equação com condições de contorno prescritas. A solução encontrada pode, então, em alguns casos, provar ser realmente uma função verdadeira e uma solução para a equação original (por exemplo, usando o teorema de Lax-Milgram , uma consequência do teorema de representação de Riesz ).
Análise de Fourier
Resolver uma função periódica em uma soma de funções trigonométricas forma uma série de Fourier , uma técnica muito usada em física e engenharia. O espaço vetorial subjacente é geralmente o espaço de Hilbert L 2 (0, 2π), para o qual as funções sin ( mx ) e cos ( mx ) (onde m é um inteiro) formam uma base ortogonal. A expansão de Fourier de uma função L 2 f é
Os coeficientes a m e b m são chamados de coeficientes de Fourier de f , e são calculados pelas fórmulas
- ,
Em termos físicos, a função é representada como uma superposição de ondas senoidais e os coeficientes fornecem informações sobre o espectro de frequência da função . Uma forma de número complexo da série de Fourier também é comumente usada. As fórmulas concretas acima são consequências de uma dualidade matemática mais geral chamada dualidade de Pontryagin . Aplicado ao grupo R , produz a transformada clássica de Fourier; uma aplicação em física são redes recíprocas , onde o grupo subjacente é um espaço vetorial real de dimensão finita dotado do datum adicional de uma rede que codifica as posições dos átomos nos cristais .
As séries de Fourier são usadas para resolver problemas de valor limite em equações diferenciais parciais . Em 1822, Fourier usou essa técnica pela primeira vez para resolver a equação do calor . Uma versão discreta da série de Fourier pode ser usada em aplicações de amostragem onde o valor da função é conhecido apenas em um número finito de pontos igualmente espaçados. Nesse caso, a série de Fourier é finita e seu valor é igual aos valores amostrados em todos os pontos. O conjunto de coeficientes é conhecido como transformada discreta de Fourier (DFT) da sequência de amostra fornecida. O DFT é uma das principais ferramentas de processamento de sinal digital , um campo cujas aplicações incluem radar , codificação de voz e compressão de imagem . O formato de imagem JPEG é uma aplicação da transformação discreta de cosseno intimamente relacionada .
A transformada rápida de Fourier é um algoritmo para calcular rapidamente a transformada discreta de Fourier. É usado não apenas para calcular os coeficientes de Fourier, mas, usando o teorema da convolução , também para calcular a convolução de duas sequências finitas. Eles, por sua vez, são aplicados em filtros digitais e como um algoritmo de multiplicação rápida para polinômios e inteiros grandes ( algoritmo de Schönhage-Strassen ).
Geometria diferencial

O plano tangente a uma superfície em um ponto é naturalmente um espaço vetorial cuja origem é identificada com o ponto de contato. O plano tangente é a melhor aproximação linear , ou linearização , de uma superfície em um ponto. Mesmo em um espaço euclidiano tridimensional, normalmente não há uma maneira natural de prescrever uma base do plano tangente e, portanto, ele é concebido como um espaço vetorial abstrato em vez de um espaço de coordenadas real. O espaço tangente é a generalização para variedades diferenciáveis de dimensões superiores .
Variedades Riemannianas são variedades cujos espaços tangentes são dotados de um produto interno adequado . Derivado daí, o tensor de curvatura de Riemann codifica todas as curvaturas de uma variedade em um objeto, que encontra aplicações na relatividade geral , por exemplo, onde o tensor de curvatura de Einstein descreve o conteúdo de matéria e energia do espaço-tempo . O espaço tangente de um grupo de Lie pode receber naturalmente a estrutura de uma álgebra de Lie e pode ser usado para classificar grupos de Lie compactos .
Generalizações
Pacotes de vetores
Um feixe de vector é uma família de espaço vectorial parametrizada contínua por um espaço topológico X . Mais precisamente, um pacote vetorial sobre X é um espaço topológico E equipado com um mapa contínuo
- π: E → X
tal que para cada x em X , a fibra π −1 ( x ) é um espaço vetorial. O caso dim V = 1 é chamado de feixe de linhas . Para qualquer espaço vetorial V , a projeção X × V → X torna o produto X × V um pacote vetorial "trivial" . Os feixes de vetores sobre X devem ser localmente um produto de X e algum espaço vetorial (fixo) V : para cada x em X , há uma vizinhança U de x tal que a restrição de π a π −1 ( U ) é isomórfica ao pacote trivial U × V → U . Apesar de seu caráter localmente trivial, os feixes de vetores podem (dependendo da forma do espaço subjacente X ) ser "torcidos" no grande (isto é, o feixe não precisa ser (globalmente isomórfico) o feixe trivial X × V ). Por exemplo, a faixa de Möbius pode ser vista como um feixe de linhas sobre o círculo S 1 ( identificando intervalos abertos com a linha real ). É, no entanto, diferente do cilindro S 1 × R , porque o último é orientável, enquanto o primeiro não o é.
As propriedades de certos pacotes vetoriais fornecem informações sobre o espaço topológico subjacente. Por exemplo, o feixe tangente consiste na coleção de espaços tangentes parametrizados pelos pontos de uma variedade diferenciável. O feixe tangente do círculo S 1 é globalmente isomórfico a S 1 × R , uma vez que existe um campo vetorial não nulo global em S 1 . Em contraste, pelo teorema da bola cabeluda , não há campo vetorial (tangente) na 2-esfera S 2, que é em todo lugar diferente de zero. A teoria K estuda as classes de isomorfismo de todos os feixes de vetores em algum espaço topológico. Além aprofundamento visão topológica e geométrica, tem consequências puramente algébricos, tais como a classificação de bens de dimensão finita álgebra de divisão : R , C , a quatérnions H e o octoniones ó .
O feixe cotangente de uma variedade diferenciável consiste, em todos os pontos da variedade, do dual do espaço tangente, o espaço cotangente . As seções desse pacote são conhecidas como formas únicas diferenciais .
Módulos
Os módulos estão para os anéis o que os espaços vetoriais estão para os campos: os mesmos axiomas, aplicados a um anel R em vez de um campo F , geram módulos. A teoria dos módulos, comparada com a dos espaços vetoriais, é complicada pela presença de elementos de anel que não possuem inversos multiplicativos . Por exemplo, os módulos não precisam ter bases, como mostra o módulo Z (isto é, o grupo abeliano ) Z / 2 Z ; os módulos que o fazem (incluindo todos os espaços vetoriais) são conhecidos como módulos livres . No entanto, um espaço vetorial pode ser definido compactamente como um módulo sobre um anel que é um campo , sendo os elementos chamados de vetores. Alguns autores usam o termo espaço vetorial para significar módulos sobre um anel de divisão . A interpretação algebro-geométrica de anéis comutativos por meio de seu espectro permite o desenvolvimento de conceitos como módulos localmente livres , a contrapartida algébrica dos feixes vetoriais.
Espaços afins e projetivos
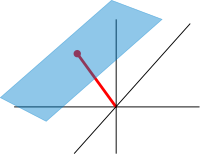
Grosso modo, os espaços afins são espaços vetoriais cujas origens não são especificadas. Mais precisamente, um espaço afim é um conjunto com uma ação de espaço vetorial transitivo livre . Em particular, um espaço vetorial é um espaço afim sobre si mesmo, pelo mapa
- V × V → V , ( v , a ) ↦ a + v .
Se W é um espaço vetorial, então um subespaço afim é um subconjunto de W obtido pela tradução de um subespaço linear V por um vetor fixo x ∈ W ; este espaço é indicado por x + V (isto é um coset de V em W ) e consiste em todos os vectores da forma x + v para v ∈ V . Um exemplo importante é o espaço de soluções de um sistema de equações lineares não homogêneas
- A x = b
generalizando o caso homogêneo acima , que pode ser encontrado definindo b = 0 nesta equação. O espaço de soluções é o subespaço afim x + V onde x é uma solução particular da equação, e V é o espaço de soluções da equação homogênea (o espaço nulo de A ).
O conjunto de subespaços unidimensionais de um espaço vetorial de dimensão finita V é conhecido como espaço projetivo ; pode ser usado para formalizar a ideia de linhas paralelas que se cruzam no infinito. Grassmannianos e variedades de sinalizadores generalizam isso parametrizando subespaços lineares de dimensão fixa k e sinalizadores de subespaços, respectivamente.
Veja também
- Vetor (matemática e física) , para uma lista de vários tipos de vetores
Notas
Citações
Referências
Álgebra
- Artin, Michael (1991), Algebra , Prentice Hall , ISBN 978-0-89871-510-1
- Blass, Andreas (1984), "Existência de bases implica o axioma da escolha", Teoria dos conjuntos axiomáticos (Boulder, Colorado, 1983) (PDF) , Contemporary Mathematics, 31 , Providence, RI: American Mathematical Society , pp. 31-33 , MR 0763890
- Brown, William A. (1991), Matrices and vector spaces , Nova York: M. Dekker, ISBN 978-0-8247-8419-5
- Lang, Serge (1987), Linear algebra , Berlin, New York: Springer-Verlag , ISBN 978-0-387-96412-6
- Lang, Serge (2002), Algebra , Graduate Texts in Mathematics , 211 (revisado, terceira edição), Nova York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556
- Mac Lane, Saunders (1999), Algebra (3ª ed.), Pp. 193-222, ISBN 978-0-8218-1646-2
- Meyer, Carl D. (2000), Matrix Analysis and Applied Linear Algebra , SIAM , ISBN 978-0-89871-454-8
- Roman, Steven (2005), Advanced Linear Algebra , Graduate Texts in Mathematics, 135 (2ª ed.), Berlim, Nova York: Springer-Verlag , ISBN 978-0-387-24766-3
- Spindler, Karlheinz (1993), Abstract Algebra with Applications: Volume 1: Vector Spaces and Groups , CRC, ISBN 978-0-8247-9144-5
- van der Waerden, Bartel Leendert (1993), Algebra (em alemão) (9ª ed.), Berlim, Nova York: Springer-Verlag , ISBN 978-3-540-56799-8
Análise
- Bourbaki, Nicolas (1987), Espaços vetoriais topológicos , Elementos da matemática, Berlim, Nova York: Springer-Verlag , ISBN 978-3-540-13627-9
- Bourbaki, Nicolas (2004), Integration I , Berlin, New York: Springer-Verlag , ISBN 978-3-540-41129-1
- Braun, Martin (1993), Equações diferenciais e suas aplicações: uma introdução à matemática aplicada , Berlim, Nova York: Springer-Verlag , ISBN 978-0-387-97894-9
- BSE-3 (2001) [1994], "Tangent plane" , Encyclopedia of Mathematics , EMS Press
- Choquet, Gustave (1966), Topology , Boston, MA: Academic Press
- Dennery, Philippe; Krzywicki, Andre (1996), Mathematics for Physicists , Courier Dover Publications, ISBN 978-0-486-69193-0
- Dudley, Richard M. (1989), Análise real e probabilidade , The Wadsworth & Brooks / Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks / Cole Advanced Books & Software, ISBN 978-0-534-10050-6
- Dunham, William (2005), The Calculus Gallery , Princeton University Press , ISBN 978-0-691-09565-3
- Evans, Lawrence C. (1998), Equações diferenciais parciais , Providence, RI: American Mathematical Society , ISBN 978-0-8218-0772-9
- Folland, Gerald B. (1992), Fourier Analysis and Its Applications , Brooks-Cole, ISBN 978-0-534-17094-3
- Gasquet, Claude; Witomski, Patrick (1999), Fourier Analysis and Applications: Filtering, Numerical Computation, Wavelets , Texts in Applied Mathematics, Nova York: Springer-Verlag, ISBN 978-0-387-98485-8
- Ifeachor, Emmanuel C .; Jervis, Barrie W. (2001), Digital Signal Processing: A Practical Approach (2ª ed.), Harlow, Essex, England: Prentice-Hall (publicado em 2002), ISBN 978-0-201-59619-9
- Krantz, Steven G. (1999), A Panorama of Harmonic Analysis , Carus Mathematical Monographs, Washington, DC: Mathematical Association of America, ISBN 978-0-88385-031-2
- Kreyszig, Erwin (1988), Advanced Engineering Mathematics (6ª ed.), Nova York: John Wiley & Sons, ISBN 978-0-471-85824-9
- Kreyszig, Erwin (1989), Análise funcional introdutória com aplicações , Wiley Classics Library, Nova York: John Wiley & Sons , ISBN 978-0-471-50459-7, MR 0992618
- Lang, Serge (1983), Real analysis , Addison-Wesley , ISBN 978-0-201-14179-5
- Lang, Serge (1993), Real and Functional analysis , Berlin, New York: Springer-Verlag , ISBN 978-0-387-94001-4
- Loomis, Lynn H. (1953), Uma introdução à análise harmônica abstrata , Toronto-Nova York-Londres: D. Van Nostrand Company, Inc., pp. X + 190, hdl : 2027 / uc1.b4250788
- Narici, Lawrence ; Beckenstein, Edward (2011). Espaços vetoriais topológicos . Matemática pura e aplicada (segunda edição). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834 .
- Schaefer, Helmut H .; Wolff, Manfred P. (1999). Espaços vetoriais topológicos . GTM . 8 (segunda edição). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135 .
- Treves, François (1967), Topological vector spaces, distributions and kernels , Boston, MA: Academic Press
Referências históricas
- Banach, Stefan (1922), "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operation in abstract sets and your application to integ equations)" (PDF) , Fundamenta Mathematicae (em francês), 3 : 133– 181, doi : 10.4064 / fm-3-1-133-181 , ISSN 0016-2736
- Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerações sobre alguns aspectos da geometria elementar) (em alemão)
- Bellavitis, Giuso (1833), "Sopra alcune applicazioni di un nuovo metodo di geometria analitica", Il poligrafo giornale di scienze, lettre ed arti , Verona, 13 : 53-61.
- Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elementos da história da matemática) (em francês), Paris: Hermann
- Dorier, Jean-Luc (1995), "Um esboço geral da gênese da teoria do espaço vetorial" , Historia Mathematica , 22 (3): 227-261, doi : 10.1006 / hmat.1995.1024 , MR 1347828
- Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (em francês), Chez Firmin Didot, père et fils
- Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (em alemão), O. Wigand, reimpressão: Grassmann, Hermann (2000), Kannenberg, LC (ed.), Extension Theory , traduzido por Kannenberg, Lloyd C., Providence, RI: American Mathematical Society , ISBN 978-0-8218-2031-5
- Hamilton, William Rowan (1853), Lectures on Quaternions , Royal Irish Academy
- Möbius, August Ferdinand (1827), Der Barycentrische Calcul: ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (cálculo baricêntrico: uma nova utilidade para um tratamento analítico da geometria) (em alemão), arquivado do original em 2006-11-23
- Moore, Gregory H. (1995), "The axiomatization of linear algebra: 1875-1940", Historia Mathematica , 22 (3): 262-303, doi : 10.1006 / hmat.1995.1025
- Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (em italiano), Torino
- Peano, G. (1901) Formulario mathematico : axiomas vct via Internet Archive
Outras referências
- Ashcroft, Neil ; Mermin, N. David (1976), Solid State Physics , Toronto: Thomson Learning, ISBN 978-0-03-083993-1
- Atiyah, Michael Francis (1989), teoria K , Advanced Book Classics (2ª ed.), Addison-Wesley , ISBN 978-0-201-09394-0, MR 1043170
- Bourbaki, Nicolas (1998), Elements of Mathematics: Algebra I Chapters 1-3 , Berlin, New York: Springer-Verlag , ISBN 978-3-540-64243-5
- Bourbaki, Nicolas (1989), General Topology. Capítulos 1-4 , Berlim, Nova York: Springer-Verlag , ISBN 978-3-540-64241-1
- Coxeter, Harold Scott MacDonald (1987), Projective Geometry (2ª ed.), Berlin, New York: Springer-Verlag , ISBN 978-0-387-96532-1
- Eisenberg, Murray; Guy, Robert (1979), "Uma prova do teorema da bola cabeluda", The American Mathematical Monthly , 86 (7): 572-574, doi : 10.2307 / 2320587 , JSTOR 2320587
- Eisenbud, David (1995), Commutative algebra , Graduate Texts in Mathematics, 150 , Berlim, Nova York: Springer-Verlag , ISBN 978-0-387-94269-8, MR 1322960
- Goldrei, Derek (1996), Teoria dos Conjuntos Clássicos: Um estudo independente guiado (1ª ed.), Londres: Chapman and Hall , ISBN 978-0-412-60610-6
- Griffiths, David J. (1995), Introdução à Mecânica Quântica , Upper Saddle River, NJ: Prentice Hall , ISBN 978-0-13-124405-4
- Halmos, Paul R. (1974), espaços vetoriais de dimensão finita , Berlim, Nova York: Springer-Verlag , ISBN 978-0-387-90093-3
- Halpern, James D. (junho de 1966), "Bases in Vector Spaces and the Axiom of Choice", Proceedings of the American Mathematical Society , 17 (3): 670-673, doi : 10.2307 / 2035388 , JSTOR 2035388
- Hughes-Hallett, Deborah; McCallum, William G .; Gleason, Andrew M. (2013), Calculus: Single and Multivariable (6 ed.), John Wiley & Sons , ISBN 978-0470-88861-2
- Husemoller, Dale (1994), Fiber Bundles (3rd ed.), Berlin, New York: Springer-Verlag , ISBN 978-0-387-94087-8
- Jost, Jürgen (2005), Riemannian Geometry and Geometric Analysis (4ª ed.), Berlim, Nova York: Springer-Verlag , ISBN 978-3-540-25907-7
- Kreyszig, Erwin (1991), Geometria diferencial , Nova York: Dover Publications , pp. Xiv + 352, ISBN 978-0-486-66721-8
- Kreyszig, Erwin (1999), Advanced Engineering Mathematics (8ª ed.), Nova York: John Wiley & Sons , ISBN 978-0-471-15496-9
- Luenberger, David (1997), Otimização por métodos de espaço vetorial , Nova York: John Wiley & Sons , ISBN 978-0-471-18117-0
- Mac Lane, Saunders (1998), Categories for the Working Mathematician (2ª ed.), Berlim, Nova York: Springer-Verlag , ISBN 978-0-387-98403-2
- Misner, Charles W .; Thorne, Kip ; Wheeler, John Archibald (1973), Gravitation , WH Freeman, ISBN 978-0-7167-0344-0
- Naber, Gregory L. (2003), The geometry of Minkowski spacetime , New York: Dover Publications , ISBN 978-0-486-43235-9, MR 2044239
- Schönhage, A .; Strassen, Volker (1971), "Schnelle Multiplikation großer Zahlen (Fast multiplation of big numbers)", Computing (in German), 7 (3-4): 281-292, doi : 10.1007 / bf02242355 , ISSN 0010-485X , S2CID 9738629
- Spivak, Michael (1999), A Comprehensive Introduction to Differential Geometry (Volume Two) , Houston, TX: Publish or Perish
- Stewart, Ian (1975), Galois Theory , Chapman and Hall Mathematics Series, London: Chapman and Hall , ISBN 978-0-412-10800-6
- Varadarajan, VS (1974), grupos de Lie, álgebras de Lie e suas representações , Prentice Hall , ISBN 978-0-13-535732-3
- Wallace, GK (fevereiro de 1992), "The JPEG still picture compression standard" (PDF) , IEEE Transactions on Consumer Electronics , 38 (1): xviii – xxxiv, CiteSeerX 10.1.1.318.4292 , doi : 10.1109 / 30.125072 , ISSN 0098 -3063 , arquivado do original (PDF) em 13/01/2007 , recuperado em 25/10/2017
- Weibel, Charles A. (1994). Uma introdução à álgebra homológica . Cambridge Studies in Advanced Mathematics. 38 . Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324 . OCLC 36131259 .
links externos
- "Vector space" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]













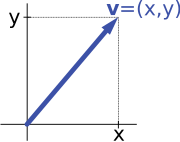






















































![{\ frac {a_ {0}} {2}} + \ sum _ {m = 1} ^ {\ infty} \ left [a_ {m} \ cos \ left (mx \ right) + b_ {m} \ sin \ left (mx \ right) \ right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/b02fb26ebada4babaa1d88e20bb63e3b370c13b3)


