Embalagem de esfera - Sphere packing

O empacotamento de esferas encontra aplicação prática no empilhamento de balas de canhão

Em geometria , um empacotamento de esfera é um arranjo de esferas não sobrepostas dentro de um espaço de contenção. As esferas consideradas são geralmente de tamanho idêntico, e o espaço é geralmente um espaço euclidiano tridimensional . No entanto, os problemas de empacotamento de esferas podem ser generalizados para considerar esferas desiguais, espaços de outras dimensões (onde o problema se torna empacotamento de círculos em duas dimensões ou empacotamento de hiperesferas em dimensões superiores) ou para espaços não euclidianos , como o espaço hiperbólico .

Um problema típico de empacotamento de esferas é encontrar um arranjo no qual as esferas preencham o máximo possível do espaço. A proporção do espaço preenchido pelas esferas é chamada de densidade do arranjo. Como a densidade local de um empacotamento em um espaço infinito pode variar dependendo do volume sobre o qual é medido, o problema geralmente é maximizar a densidade média ou assintótica , medida em um volume grande o suficiente.

Para esferas iguais em três dimensões, o empacotamento mais denso usa aproximadamente 74% do volume. Um empacotamento aleatório de esferas iguais geralmente tem uma densidade em torno de 64%.

Classificação e terminologia

Um arranjo de rede (comumente chamado de arranjo regular ) é aquele em que os centros das esferas formam um padrão muito simétrico que precisa de apenas n vetores para ser definido de forma única (no espaço euclidiano n - dimensional ). Os arranjos de treliça são periódicos. Arranjos nos quais as esferas não formam uma rede (freqüentemente referida como irregular ) podem ainda ser periódicos, mas também aperiódicos (propriamente falando não periódicos ) ou aleatórios . Arranjos reticulados são mais fáceis de manusear do que os irregulares - seu alto grau de simetria torna mais fácil classificá-los e medir suas densidades.

Embalagem regular

Arranjo regular de esferas iguais em um plano mudando para um arranjo irregular de esferas desiguais (bolhas).

A rede HCP (esquerda) e a rede FCC (direita) são os dois arranjos de densidade mais alta mais comuns.

Duas maneiras de empilhar três aviões feitos de esferas

Embalagem densa

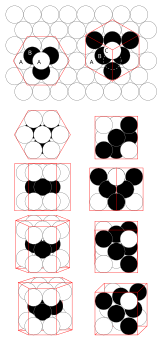
No espaço euclidiano tridimensional, o empacotamento mais denso de esferas iguais é obtido por uma família de estruturas chamadas de estruturas compactadas . Um método para gerar tal estrutura é o seguinte. Considere um plano com um arranjo compacto de esferas. Chame-o de A. Para quaisquer três esferas vizinhas, uma quarta esfera pode ser colocada no topo da cavidade entre as três esferas inferiores. Se fizermos isso para metade dos furos em um segundo plano acima do primeiro, criaremos uma nova camada compacta. Existem duas escolhas possíveis para fazer isso, chame-as de B e C. Suponha que escolhemos B. Então, metade das cavidades de B está acima dos centros das bolas em A e a outra metade está acima das cavidades de A que não foram usado para B. Assim, as bolas de uma terceira camada podem ser colocadas diretamente acima das bolas da primeira, produzindo uma camada do tipo A, ou acima dos orifícios da primeira camada que não foram ocupados pela segunda camada, produzindo um camada do tipo C. A combinação das camadas dos tipos A, B e C produz várias estruturas compactadas.

Dois arranjos simples dentro de uma família compacta correspondem a redes regulares. Um é chamado de empacotamento cúbico fechado (ou cúbico de face centrada , "FCC") - onde as camadas são alternadas na seqüência ABCABC .... O outro é chamado de empacotamento hexagonal fechado ("HCP") - onde as camadas são alternadas na seqüência ABAB .... Mas muitas sequências de empilhamento de camadas são possíveis (ABAC, ABCBA, ABCBAC, etc.) e ainda geram uma estrutura compacta. Em todos esses arranjos, cada esfera toca 12 esferas vizinhas, e a densidade média é

${\ displaystyle {\ frac {\ pi} {3 {\ sqrt {2}}}} \ simeq 0.74048.}$

Carl Friedrich Gauss provou em 1831 que essas embalagens têm a maior densidade entre todas as embalagens treliçadas possíveis.

Em 1611, Johannes Kepler conjecturou que esta é a densidade máxima possível entre arranjos regulares e irregulares - isso ficou conhecido como a conjectura de Kepler . Em 1998, Thomas Callister Hales , seguindo a abordagem sugerida por László Fejes Tóth em 1953, anunciou uma prova da conjectura de Kepler. A prova de Hales é uma prova por exaustão envolvendo a verificação de muitos casos individuais usando cálculos complexos de computador. Os árbitros disseram que estavam "99% certos" da correção da prova de Hales. Em 10 de agosto de 2014, a Hales anunciou a conclusão de uma prova formal usando verificação de prova automatizada , eliminando qualquer dúvida.

Outras embalagens de treliça comuns

Algumas outras embalagens de treliça são freqüentemente encontradas em sistemas físicos. Estes incluem a rede cúbica com uma densidade de , a rede hexagonal com uma densidade de e a rede tetraédrica com uma densidade de , e a mais frouxa possível em uma densidade de 0,0555. ${\ displaystyle {\ frac {\ pi} {6}} \ aproximadamente 0,5236}$${\ displaystyle {\ frac {\ pi} {3 {\ sqrt {3}}}} \ approx 0,6046}$${\ displaystyle {\ frac {\ pi {\ sqrt {3}}} {16}} \ approx 0.3401}$

Embalagens atoladas com baixa densidade

As embalagens em que todas as esferas são restringidas por seus vizinhos para permanecer em um local são chamadas de rígidas ou emperradas . O empacotamento da esfera estritamente congestionado com a densidade mais baixa é um cristal Fcc diluído ("tunelado") com uma densidade de apenas 0,49365.

Embalagem irregular

Se tentarmos construir uma coleção densamente compactada de esferas, seremos tentados a sempre colocar a próxima esfera em um oco entre três esferas compactadas. Se cinco esferas forem montadas desta forma, elas serão consistentes com um dos arranjos regularmente embalados descritos acima. No entanto, a sexta esfera colocada desta forma tornará a estrutura inconsistente com qualquer arranjo regular. Isso resulta na possibilidade de um empacotamento aleatório de esferas que é estável contra compressão. A vibração de uma embalagem solta aleatória pode resultar no arranjo de partículas esféricas em embalagens regulares, um processo conhecido como cristalização granular . Esses processos dependem da geometria do recipiente que contém os grãos esféricos.

Quando as esferas são adicionadas aleatoriamente a um contêiner e depois comprimidas, elas geralmente formam o que é conhecido como configuração de embalagem "irregular" ou "emperrada" quando não podem mais ser comprimidas. Este empacotamento irregular geralmente terá uma densidade de cerca de 64%. Uma pesquisa recente prevê analiticamente que não pode exceder um limite de densidade de 63,4%. Esta situação é diferente do caso de uma ou duas dimensões, onde compactar uma coleção de esferas unidimensionais ou bidimensionais (ou seja, segmentos de linha ou círculos) resultará uma embalagem normal.

Empacotamento hiperesférico

O problema de empacotamento de esferas é a versão tridimensional de uma classe de problemas de empacotamento de esferas em dimensões arbitrárias. Em duas dimensões, o problema equivalente é compactar círculos em um plano. Em uma dimensão, ele está empacotando segmentos de linha em um universo linear.

Em dimensões superiores a três, as embalagens regulares mais densas de hiperesferas são conhecidas até 8 dimensões. Muito pouco se sabe sobre embalagens de hiperesferas irregulares; é possível que em algumas dimensões o empacotamento mais denso seja irregular. Algum suporte para esta conjectura vem do fato de que em certas dimensões (por exemplo, 10) o empacotamento irregular conhecido mais denso é mais denso do que o empacotamento regular mais denso conhecido.

Em 2016, Maryna Viazovska anunciou uma prova de que a rede E ₈ fornece o empacotamento ideal (independentemente da regularidade) no espaço de oito dimensões, e logo depois ela e um grupo de colaboradores anunciaram uma prova semelhante de que a rede Leech é ótima em 24 dimensões . Este resultado construiu e melhorou métodos anteriores que mostraram que essas duas redes estão muito próximas do ótimo. As novas provas envolvem o uso da transformada de Laplace de uma função modular cuidadosamente escolhida para construir uma função radialmente simétrica f tal que f e sua transformada de Fourier f̂ ambas iguais na origem , e ambas desaparecem em todos os outros pontos da rede ótima, com f negativo fora da esfera central da embalagem e f̂ positivo. Então, a fórmula de soma de Poisson para f é usada para comparar a densidade da rede ótima com a de qualquer outro empacotamento. Antes que a prova fosse oficialmente avaliada e publicada, o matemático Peter Sarnak chamou a prova de "incrivelmente simples" e escreveu: "Você apenas começa a ler o artigo e sabe que está correto".

Outra linha de pesquisa em grandes dimensões está tentando encontrar limites assintóticos para a densidade das embalagens mais densas. A partir de 2017, sabe-se que para n grande , a rede mais densa na dimensão n tem densidade entre cn ⋅ 2 ^{- n} (para alguma constante c ) e 2 ^{−0,599 n} . Os limites conjecturais estão entre os dois.

Empacotamento de esfera desigual

Um empacotamento denso de esferas com uma razão de raio de 0,64799 e uma densidade de 0,74786

Muitos problemas nas ciências químicas e físicas podem estar relacionados a problemas de empacotamento onde mais de um tamanho de esfera está disponível. Aqui, há uma escolha entre separar as esferas em regiões de esferas iguais compactadas ou combinar os vários tamanhos de esferas em um composto ou embalagem intersticial . Quando muitos tamanhos de esferas (ou uma distribuição ) estão disponíveis, o problema rapidamente se torna intratável, mas alguns estudos de esferas rígidas binárias (dois tamanhos) estão disponíveis.

Quando a segunda esfera é muito menor do que a primeira, é possível organizar as grandes esferas em um arranjo compacto e, em seguida, organizar as pequenas esferas dentro das lacunas octaédrica e tetraédrica. A densidade desse empacotamento intersticial depende sensivelmente da relação do raio, mas no limite das relações de tamanho extremas, as esferas menores podem preencher as lacunas com a mesma densidade que as esferas maiores preencheram o espaço. Mesmo se as esferas grandes não estiverem em um arranjo compactado, sempre é possível inserir algumas esferas menores de até 0,29099 do raio da esfera maior.

Quando a esfera menor tem um raio maior do que 0,41421 do raio da esfera maior, não é mais possível caber nem mesmo nos orifícios octaédricos da estrutura compacta. Assim, além desse ponto, a estrutura do hospedeiro deve se expandir para acomodar os intersticiais (o que compromete a densidade geral) ou se reorganizar em uma estrutura de composto cristalino mais complexa. São conhecidas estruturas que excedem a densidade de empacotamento próxima para razões de raio de até 0,659786.

Os limites superiores para a densidade que podem ser obtidos em tais embalagens binárias também foram obtidos.

Em muitas situações químicas, como cristais iônicos , a estequiometria é restringida pelas cargas dos íons constituintes. Esta restrição adicional no empacotamento, junto com a necessidade de minimizar a energia Coulomb de cargas interagentes leva a uma diversidade de arranjos de empacotamento ótimos.

Espaço hiperbólico

Embora o conceito de círculos e esferas possa ser estendido ao espaço hiperbólico , encontrar o empacotamento mais denso se torna muito mais difícil. Em um espaço hiperbólico, não há limite para o número de esferas que podem circundar outra esfera (por exemplo, os círculos de Ford podem ser pensados ​​como um arranjo de círculos hiperbólicos idênticos em que cada círculo é circundado por um número infinito de outros círculos). O conceito de densidade média também se torna muito mais difícil de definir com precisão. Os pacotes mais densos em qualquer espaço hiperbólico são quase sempre irregulares.

Apesar desta dificuldade, K. Böröczky fornece um limite superior universal para a densidade de empacotamento de esferas do espaço n hiperbólico onde n  ≥ 2. Em três dimensões, o limite de Böröczky é de aproximadamente 85,327613%, e é realizado pelo empacotamento de horosfera da ordem- 6 favo de mel tetraédrico com o símbolo Schläfli {3,3,6}. Além desta configuração, pelo menos três outros pacotes de horosfera são conhecidos por existirem no espaço 3 hiperbólico que realizam o limite superior de densidade.

Pares tocantes, trigêmeos e quádruplos

O gráfico de contato de um empacotamento finito arbitrário de bolas unitárias é o gráfico cujos vértices correspondem aos elementos de empacotamento e cujos dois vértices são conectados por uma aresta se os dois elementos de empacotamento correspondentes se tocam. A cardinalidade do conjunto de arestas do gráfico de contato fornece o número de pares em contato, o número de 3 ciclos no gráfico de contato fornece o número de tripletos em contato e o número de tetraedros no gráfico de contato fornece o número de quádruplos em contato ( em geral, para um gráfico de contato associado a um empacotamento de esferas em n dimensões, a cardinalidade do conjunto de n -simplices no gráfico de contato fornece o número de ( n  + 1) -tuples de contato no empacotamento de esferas). No caso do espaço euclidiano tridimensional, os limites superiores não triviais do número de pares, trigêmeos e quádruplos que se tocam foram provados por Karoly Bezdek e Samuel Reid na Universidade de Calgary.

O problema de encontrar o arranjo de n esferas idênticas que maximiza o número de pontos de contato entre as esferas é conhecido como o "problema das esferas pegajosas". O máximo é conhecido para n ≤ 11, e apenas valores conjecturais são conhecidos para n maior .

Outros espaços

O empacotamento de esferas nos cantos de um hipercubo (com as esferas definidas pela distância de Hamming ) corresponde ao projeto de códigos de correção de erros : se as esferas têm raio t , então seus centros são palavras-código de um código de correção de erro (2 t  + 1) . As embalagens reticuladas correspondem a códigos lineares. Existem outras relações mais sutis entre o empacotamento da esfera euclidiana e os códigos de correção de erros. Por exemplo, o código binário de Golay está intimamente relacionado à rede Leech de 24 dimensões.

Para obter mais detalhes sobre essas conexões, consulte o livro Sphere Packings, Lattices and Groups de Conway e Sloane .

Veja também

• Empacotamento de esferas iguais
• Empacotamento da esfera apolínea
• Constante de Hermite
• Esfera inscrita
• Problema de número de beijos
• Limite de empacotamento de esfera
• Pacote de fechamento aleatório
• Embalagem da esfera do cilindro

Referências

Bibliografia

• Aste, T .; Weaire, D. (2000). A Busca da Embalagem Perfeita . Londres: Institute of Physics Publishing. ISBN 0-7503-0648-3.
• Conway, JH ; Sloane, NJH (1998). Sphere Packings, Lattices and Groups (3ª ed.). ISBN 0-387-98585-9.
• Sloane, NJA (1984). "O Empacotamento de Esferas". Scientific American . 250 : 116–125. Bibcode : 1984SciAm.250e.116G . doi : 10.1038 / scientificamerican0584-116 .

links externos

• Dana Mackenzie (maio de 2002) " A fine mess " (New Scientist)

Uma visão geral não técnica do empacotamento no espaço hiperbólico.

• Weisstein, Eric W. "Circle Packing" . MathWorld .
• "Kugelpackungen (embalagem de esfera)" (TE Dorozinski)
• "3D Sphere Packing Applet" Applet Java Sphere Packing
• "Densest Packing of spheres in a sphere" applet java
• "Banco de dados de embalagens de esferas" (Erik Agrell)