Permutoedro - Permutohedron

O permutoedro de ordem 4

Em matemática , o permutoedro de ordem n é um politopo ( n - 1) -dimensional embutido em um espaço n- dimensional. Suas coordenadas de vértice (rótulos) são as permutações dos primeiros n números naturais . As arestas identificam os caminhos mais curtos possíveis (conjuntos de transposições ) que conectam dois vértices (permutações). Duas permutações conectadas por uma aresta diferem em apenas dois lugares (uma transposição ), e os números nesses lugares são vizinhos (diferem em valor por 1).

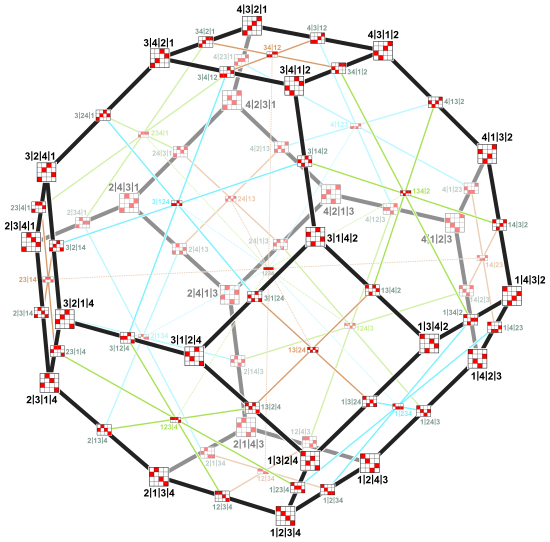
A imagem à direita mostra o permutoedro de ordem 4, que é o octaedro truncado . Seus vértices são as 24 permutações de (1, 2, 3, 4). Bordas paralelas têm a mesma cor de borda. As 6 cores de borda correspondem às 6 transposições possíveis de 4 elementos, ou seja, indicam em quais dois lugares as permutações conectadas diferem. (Por exemplo, bordas vermelhas conectam permutações que diferem nos dois últimos lugares.)

História

De acordo com Günter M. Ziegler ( 1995 ), os permutohedra foram estudados pela primeira vez por Pieter Hendrik Schoute ( 1911 ). O nome permutoèdre foi cunhado por Georges Th. Guilbaud e Pierre Rosenstiehl ( 1963 ). Eles descrevem a palavra como bárbara, mas fácil de lembrar, e a submetem à crítica de seus leitores.

A grafia alternativa permut a hedron também é usada às vezes. Os permutoedros são às vezes chamados de politopos de permutação , mas essa terminologia também é usada para o politopo de Birkhoff relacionado , definido como o casco convexo das matrizes de permutação . De maneira mais geral, V. Joseph Bowman ( 1972 ) usa esse termo para qualquer politopo cujos vértices tenham uma bijeção com as permutações de algum conjunto.

Vértices, arestas e facetas

vértices , arestas , facetas , faces
Dimensão da face

d = n - k

.

   k = 1    2    3    4    5
n
1      1                               1
2      1    2                          3
3      1    6    6                    13
4      1   14   36   24               75
5      1   30  150  240  120         541

O permutoedro de ordem $n$ possui $n!$ vértices, cada um dos quais adjacente a $n - 1$ outros. O número de arestas é $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} ( n - 1) n !/2$ , e seu comprimento é $\sqrt 2$ .

Dois vértices conectados diferem pela troca de duas coordenadas, cujos valores diferem por 1. O par de casas trocadas corresponde à direção da aresta. (Na imagem de exemplo, os vértices $(3, 2, 1, 4)$ e $(2, 3, 1, 4)$ são conectados por uma borda azul e diferem trocando 2 e 3 nos dois primeiros lugares. Os valores 2 e 3 diferem por 1. Todas as bordas azuis correspondem a trocas de coordenadas nos dois primeiros lugares.)

O número de facetas é $2 n - 2$ , porque correspondem a subconjuntos próprios não vazios $S$ de ${1 ... n}$ . Os vértices de uma faceta correspondente ao subconjunto $S$ têm em comum que suas coordenadas em lugares em $S$ são menores que o resto .

Exemplos de facetas
Para a ordem 3, as facetas são as 6 arestas e, para a ordem 4, são as 14 faces . As coordenadas nos lugares $i$ onde $i \in S$ são marcadas com um fundo escuro. Pode-se ver que eles são menores do que o resto. O quadrado no topo corresponde ao subconjunto ${3, 4}$ . Em seus quatro vértices, as coordenadas nos dois últimos lugares têm os menores valores (a saber, 1 e 2).
pedido 3		pedido 4
Subconjuntos de 1 elemento	Subconjuntos de 2 elementos	Subconjuntos de 1 elemento	Subconjuntos de 2 elementos	Subconjuntos de 3 elementos

De forma mais geral, as faces de dimensões 0 (vértices) a $n - 1$ (o próprio permutoedro) correspondem às ordens estritamente fracas do conjunto ${1 ... n}$ . Portanto, o número de todas as faces é o $n-$ ésimo número de Bell ordenado . Uma face de dimensão $d$ corresponde a uma ordenação com $k = n - d$ classes de equivalência.

Exemplos de rosto

pedido 3

pedido 4

$Pedidos fracos 3 Hasse.svg$

$Pedidos fracos 4 Hasse.svg$

As imagens acima mostram as redes de faces dos permutohedra de ordem 3 e 4 (sem as faces vazias) .
Cada centro da face é rotulado com uma ordem estrita e fraca. Por exemplo, o quadrado no topo como 3 4 | 1 2 , que representa $({3, 4}, {1, 2})$ .
Os pedidos são parcialmente solicitados por refinamento , com os mais finos do lado de fora.
Mover-se ao longo de uma aresta em direção ao interior significa mesclar duas classes de equivalência vizinhas.

Os rótulos dos vértices a | b | c | d interpretados como permutações (a, b, c, d) são aqueles que formam o gráfico de Cayley.

Facetas entre os rostos
As facetas mencionadas anteriormente estão entre essas faces e correspondem a ordenações com duas classes de equivalência. O primeiro é usado como o subconjunto $S$ atribuído à faceta, então a ordem é $(S, S c)$ . As imagens abaixo mostram como as facetas do $n$ correspondem -permutohedron ao simplical projecção do $n$ - cubo . Os rótulos de coordenadas binárias correspondem aos subconjuntos $S$ , por exemplo, 0011 a ${3, 4}$ . (O vértice projetado para o centro não corresponde a uma faceta. Nem seu vértice oposto no cubo $n$ , que não faz parte da projeção.)

O número de faces de dimensão $d = n - k$ no permutoedro de ordem $n$ é dado pelo triângulo $T$ (sequência A019538 no OEIS ): com a representação dos números de Stirling do segundo tipo É mostrado à direita junto com sua linha somas, os números ordenados da Bell .
${\ displaystyle T (n, k) = k! \ cdot \ left \ {{n \ sobre k} \ right \}}$ ${\ displaystyle \ textstyle \ left \ {{n \ atop k} \ right \}}$

Outras propriedades

O gráfico de Cayley do tipo permutoedro de S ₄ (veja aqui uma comparação com o permutoedro)

O permutoedro é transitivo ao vértice : o grupo simétrico S _n atua no permutoedro por permutação de coordenadas.

O permutoedro é um zonotopo ; uma cópia traduzida do permutoedro pode ser gerada como a soma de Minkowski dos n ( n - 1) / 2 segmentos de linha que conectam os pares dos vetores de base padrão .

Os vértices e arestas do permutoedro são isomórficos a um dos grafos de Cayley do grupo simétrico , ou seja, aquele gerado pelas transposições que trocam elementos consecutivos. Os vértices do gráfico de Cayley são as permutações inversas daquelas no permutoedro. A imagem à direita mostra o gráfico de Cayley de S 4 . Suas cores de borda representam as 3 transposições geradoras: (1, 2) , (2, 3) , (3, 4)

Este gráfico de Cayley é hamiltoniano ; um ciclo hamiltoniano pode ser encontrado pelo algoritmo Steinhaus-Johnson-Trotter .

Tesselação do espaço

Tesselação do espaço por permutohedra de ordens 3 e 4

O permutoedro de ordem n encontra-se inteiramente no hiperplano ( n - 1 ) -dimensional que consiste em todos os pontos cujas coordenadas somam o número

1 + 2 + ... + n = n ( n + 1) / 2.

Além disso, este pode ser hiperplana azulejos por um número infinito de traduzido cópias do permutohedron. Cada um deles difere do permutoedro básico por um elemento de uma determinada rede ( n - 1) -dimensional , que consiste nas n- duplas de inteiros que somam zero e cujos resíduos (módulo n ) são todos iguais:

x ₁ + x ₂ + ... + x _n = 0

x ₁ ≡ x ₂ ≡ ... ≡ x _n (mod n ).

Esta é a estrutura , a dupla estrutura da rede raiz . Em outras palavras, o permutoedro é a célula de Voronoi para . Consequentemente, esta rede é às vezes chamada de rede permutoédrica. ${\ displaystyle A_ {n-1} ^ {*}}$ ${\ displaystyle A_ {n-1}}$ ${\ displaystyle A_ {n-1} ^ {*}}$

Assim, o permutoedro de ordem 4 mostrado acima agrupa o espaço tridimensional por translação. Aqui, o espaço tridimensional é o subespaço afim do espaço 4-dimensional R ⁴ com as coordenadas x , y , z , w que consiste nas 4 tuplas de números reais cuja soma é 10,

x + y + z + w = 10.

Pode-se verificar facilmente que, para cada um dos quatro vetores a seguir,

(1,1,1, −3), (1,1, −3,1), (1, −3,1,1) e (−3,1,1,1),

a soma das coordenadas é zero e todas as coordenadas são congruentes a 1 (mod 4). Quaisquer três desses vetores geram a rede de tradução.

As tesselações formadas dessa maneira a partir dos permutohedra de ordem 2, 3 e 4, respectivamente, são o apeirogon , a telha hexagonal regular e o favo de mel cúbico bitruncado . As tesselações duais contêm todas as facetas simplex , embora não sejam politopos regulares além da ordem-3.

Exemplos

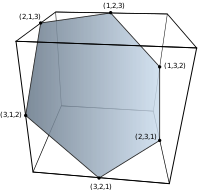
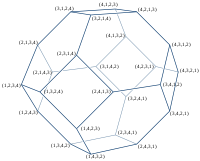
Ordem 2	Ordem 3	Pedido 4	Pedido 5	Pedido 6
2 vértices	6 vértices	24 vértices	120 vértices	720 vértices

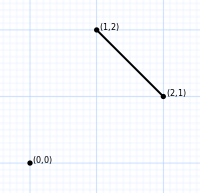
segmento de linha	hexágono	octaedro truncado	omnitruncado de 5 células	omnitruncado 5-simplex

Veja também

Notas

Referências

Baek, Jongmin; Adams, Andrew; Dolson, Jennifer (2013), "Lattice-based high-dimensional Gaussian filtering and the permutohedral lattice", Journal of Mathematical Imaging and Vision , 46 (2): 211-237, doi : 10.1007 / s10851-012-0379-2 , hdl : 1721.1 / 105344 , MR 3061550
Bowman, V. Joseph (1972), "Permutation polyhedra", SIAM Journal on Applied Mathematics , 22 (4): 580–589, doi : 10.1137 / 0122054 , JSTOR 2099695 , MR 0305800.
Gaiha, Prabha; Gupta, SK (1977), "Adjacent vertices on a permutohedron", SIAM Journal on Applied Mathematics , 32 (2): 323-327, doi : 10.1137 / 0132025 , JSTOR 2100417 , MR 0427102.
Guilbaud, Georges Th .; Rosenstiehl, Pierre (1963), "Analyze algébrique d'un scrutin" , Mathématiques et Sciences Humaines , 4 : 9-33.
Lancia, Giuseppe (2018), modelos compactos de programação linear estendida , Cham, Suíça: Springer, ISBN 978-3-319-63975-8.
Schoute, Pieter Hendrik (1911), "Tratamento analítico dos politopos regularmente derivados dos politopos regulares", Verhandelingen der Koninklijke Akademie van Wetenschappen Te Amsterdam , 11 (3): 87 pp Googlebook, 370–381 Também online na Biblioteca Digital KNAW em http://www.dwc.knaw.nl/toegangen/digital-library-knaw/?pagetype=publDetail&pId=PU00011495
Thomas, Rekha R. (2006), "Capítulo 9. The Permutahedron", Lectures in Geometric Combinatorics , Student Mathematical Library: IAS / Park City Mathematical Subseries, 33 , American Mathematical Society , pp. 85-92, ISBN 978-0-8218-4140-2.
Ziegler, Günter M. (1995), Lectures on Polytopes , Springer-Verlag, Graduate Texts in Mathematics 152.

Leitura adicional

Le Conte de Poly-Barbut, Cl. (1990), "Le diagramme du treillis permutoèdre est intersection des diagram de deux produits directs d'ordres totaux", Mathématiques, Informatique et Sciences Humaines , 112 : 49-53.
Postnikov, Alexander (2009), "Permutohedra, associahedra, and beyond", International Mathematics Research Notices (6): 1026-1106, arXiv : math.CO/0507163 , doi : 10.1093 / imrn / rnn153 , MR 2487491
Santmyer, Joe (2007), "For all possible distance look to the permutohedron", Mathematics Magazine , 80 (2): 120–125, doi : 10.1080 / 0025570X.2007.11953465

links externos

Bryan Jacobs, "Permutohedron" , MathWorld

Languages

In other projects