Mie-Gruneisen equação de estado - Mie–Gruneisen equation of state

O Mie - Gruneisen equação de estado é uma relação entre a pressão e o volume de de um sólido a uma dada temperatura. Ele é usado para determinar a pressão de um choque -compressed sólido. A relação de Mie-Gruneisen é uma forma especial do modelo Gruneisen que descreve o efeito que alterar o volume de uma estrutura de cristal tem sobre as suas propriedades vibracionais. Diversas variações da equação Mie-Gruneisen de Estado estão em uso.

O modelo Gruneisen pode ser expressa sob a forma

${\ Displaystyle \ Gama = V \ esquerda ({\ frac {DP} {de}} \ direita) _ {V}}$

onde V é o volume, P é a pressão, e é a energia interna , e Γ é o parâmetro Gruneisen que representa a pressão térmica a partir de um conjunto de átomos de vibração. Se assumirmos que Γ é independente da p e e , podemos integrar o modelo de Gruneisen para obter

${\ Displaystyle p-p_ {0} = {\ frac {\ Gamma} {V}} (e-e_ {0})}$

em que p ₀ e e ₀ são a pressão e a energia interna a um estado de referência normalmente assumido como sendo o estado, no qual a temperatura é 0K. Nesse caso, p ₀ e E ₀ são independentes da temperatura e os valores destas quantidades pode ser estimada a partir das equações Hugoniot . A equação Mie-Gruneisen de estado é uma forma especial da equação acima.

História

Gustav Mie, em 1903, desenvolveu um potencial intermolecular para derivar as equações de alta temperatura do estado de sólidos. Em 1912 Eduard Grüneisen estendido modelo de Mie para temperaturas abaixo da temperatura de Debye em que os efeitos quânticos tornam-se importantes. Forma das equações de Gruneisen é mais conveniente e tornou-se o ponto de partida habitual para derivar equações Mie-Gruneisen de Estado.

Expressões para a equação Mie-Gruneisen de Estado

Uma versão corrigido em temperatura que é usada na mecânica computacional tem a forma (ver também, p. 61)

${\ Displaystyle p = {\ frac {\ rho _ {0} C_ {0} ^ {2} \ qui \ esquerda [1 - {\ frac {\ Gamma _ {0}} {2}} \, \ qui \ direita]} {\ esquerda (1-s \ qui \ direita) ^ {2}}} + \ Gamma _ {0} E; \ quad \ qui: = 1 - {\ cfrac {\ rho _ {0}} { \ rho}}}$

onde representa a velocidade de grandes quantidades de som, é a densidade inicial, é a densidade de corrente, é gama de Gruneisen no estado de referência, é um coeficiente de inclinação Hugoniot linear, é a velocidade da onda de choque, é a velocidade da partícula, e é a energia interna por volume de referência unidade. Uma forma alternativa é ${\ Displaystyle C_ {0}}$${\ Displaystyle \ rho _ {0}}$${\ Displaystyle \ rho}$${\ Displaystyle \ Gamma _ {0}}$${\ Displaystyle s = dU_ {s} / dU_ {p}}$${\ Displaystyle U_ {s}}$${\ Displaystyle U_ {p}}$${\ Displaystyle E}$

${\ Displaystyle p = {\ frac {\ rho _ {0} C_ {0} ^ {2} (\ eta -1) \ esquerda [\ eta - {\ frac {\ _ gama {0}} {2}} (\ eta -1) \ direita]} {\ esquerda [\ eta-s (\ eta -1) \ direita] ^ {2}}} + \ _ gama {0} E; \ quad \ eta: = {\ cfrac {\ rho} {\ rho _ {0}}} \ ,.}$

Uma estimativa grosseira da energia interna pode ser calculado usando

${\ Displaystyle E = {\ frac {1} {V_ {0}}} \ int C_ {V} dT \ aprox {\ frac {C_ {v} (t-T_ {0})} {V_ {0}} } = \ rho _ {0} c_ {v} (t-T_ {0})}$

onde é o volume de referência, à temperatura , é a capacidade de calor e é a capacidade de calor específico a volume constante. Em muitas simulações, presume-se que e são iguais. ${\ Displaystyle V_ {0}}$${\ Displaystyle T = T_ {0}}$${\ Displaystyle C_ {v}}$${\ Displaystyle c_ {v}}$${\ Displaystyle C_ {p}}$${\ Displaystyle C_ {v}}$

Parâmetros para vários materiais

material	${\ Displaystyle \ rho _ {0}}$(kg / m 3 )	${\ Displaystyle c_ {v}}$ (J / kg K-)	${\ Displaystyle C_ {0}}$ (Senhora)	${\ Displaystyle s}$	${\ Displaystyle \ Gamma _ {0}}$( )${\ Displaystyle T <T_ {1}}$	${\ Displaystyle \ Gamma _ {0}}$( )${\ Displaystyle T> = T_ {1}}$	${\ Displaystyle T_ {1}}$ (K)
Cobre	8960	390	3933	1.5	1.99	2.12	700

Derivação da equação de estado

A partir do modelo de Gruneisen temos

${\ Displaystyle (1) \ qquad p-p_ {0} = {\ frac {\ Gamma} {V}} (e-e_ {0})}$

em que p ₀ e e ₀ são a pressão e a energia interna a um estado de referência. As equações Hugoniot para a conservação da massa, momento e energia são

${\ Displaystyle \ rho _ {0} U_ {s} = \ rho (U_ {s} -U_ {p}) ~~, \ quad P_ {H} -p_ {H0} = \ rho _ {0} {U_ s} U_ {p} \ quad {\ texto {e}} \ quad P_ {H} U_ {p} = \ rho _ {0} U_ {s} \ esquerda ({\ frac {U_ {p} ^ {2 }} {2}} + E_ {H} -E_ {H0} \ direita)}$

onde ρ ₀ é a densidade de referência, ρ é a densidade devido ao choque de compressão, p _H é a pressão sobre o Hugoniot, E _H é a energia interna por unidade de massa no Hugoniot, L _s é a velocidade de choque, e L _p é a velocidade da partícula. A partir da conservação de massa, nós temos

${\ Displaystyle {\ frac {U_ {p}} {U_ {s}}} = 1 - {\ frac {\ rho _ {0}} {\ rho}} = 1 - {\ frac {V} {V_ { 0}}} =: \ qui \ ,.}$

Onde nós definido , o volume específico (volume por unidade de massa). ${\ Displaystyle V = 1 / \ rho}$

Para muitos materiais L _s e L _p estão relacionadas linearmente, isto é, L _s = C ₀ + s L _p onde C ₀ e s dependem do material. Nesse caso, temos

${\ Displaystyle U_ {s} = C_ {0} + s \ qui U_ {s} \ quad {\ texto {ou}} \ quad U_ {s} = {\ frac {C_ {0}} {1-s \ chi}} \ ,.}$

A equação de impulso pode então ser escrita (para o Hugoniot principal quando p _H0 é zero) quanto

${\ Displaystyle P_ {H} = \ rho _ {0} \ qui U_ {s} ^ {2} = {\ frac {\ rho C_ {0} ^ {2} \ qui} {(1-s \ chi) ^ {2}}} \ ,.}$

Da mesma forma, a partir da equação energia que temos

${\ Displaystyle P_ {H} U_ \ qui {s} = {\ tfrac {1} {2}} \ rho \ chi ^ {2} U_ {s} ^ {3} + \ rho _ {0} U_ {s } E_ {H} = {\ tfrac {1} {2}} P_ {H} \ qui U_ {s} + \ rho _ {0} U_ {s} E_ {H} \ ,.}$

Resolvendo para e _H , temos

${\ Displaystyle E_ {H} = {\ tfrac {1} {2}} {\ frac {P_ {H} \ qui} {\ rho _ {0}}} = {\ tfrac {1} {2}} p_ {H} (V_ {0} -V)}$

Com estas expressões para p _H e E _H , o modelo Gruneisen no Hugoniot se torna

${\ Displaystyle P_ {H} -p_ {0} = {\ frac {\ Gamma} {V}} \ esquerda ({\ frac {P_ {H} \ qui V_ {0}}}} {2 - {e_ 0 } \ right) \ quad {\ text {ou}} \ quad {\ frac {\ rho C_ {0} ^ {2} \ chi} {(1-s \ chi) ^ {2}}} \ left (1 - {\ frac {\ qui} {2}} \, {\ frac {\ Gamma} {V}} \, V_ {0} \ direita) -p_ {0} = - {\ frac {\ Gamma} {V }} e_ {0} \ ,.}$

Se assumirmos que Γ / V = Γ ₀ / V ₀ e note que , obtemos ${\ Displaystyle p_ {0} = - de_ {0} / DV}$

${\ Displaystyle (2) \ qquad {\ frac {\ rho C_ {0} ^ {2} \ qui} {(1-s \ chi) ^ {2}}} \ esquerda (1 - {\ frac {\ Gamma _ {0} \ qui} {2}} \ direita) + {\ frac {de_ {0}} {dV}} + {\ frac {\ Gamma _ {0}} {V_ {0}}} e_ {0 } = 0 \} ,.$

A equação diferencial acima pode ser resolvido para e ₀ com a condição inicial e ₀ = 0 quando V = ₀ (χ = 0). A solução exata é

${\ Displaystyle {\ begin {alinhados} e_ {0} = {\ frac {\ rho C_ {0} ^ {2} V_ {0}} {2s ^ {4}}} {\ biggl [} & \ exp ( \ Gamma _ {0} \ chi) ({\ tfrac {\ Gamma _ {0}} {s}} - 3) s ^ {2} - {\ frac {[{\ tfrac {\ Gamma _ {0}} {s}} - (3-s \ chi)] s ^ {2}} {1-s \ qui}} + \\ & \ exp \ esquerda [- {\ tfrac {\ _ gama {0}} {s }} (1-s \ chi) \ direito] (\ _ gama {0} ^ {2} -4 \ _ gama {0} s + 2s ^ {2}) ({\ texto {Ei}} [{\ tfrac {\ Gamma _ {0}} {s}} (1-s \ chi)] - {\ text {Ei}} [{\ tfrac {\ Gamma _ {0}} {s}}]) {\ biggr ]} \ final {alinhados}}}$

onde Ei [Z] representa a integrante exponencial . A expressão de p ₀ é

${\ Displaystyle {\ begin {alinhados} P_ {0} = - {\ frac {de_ {0}} {dV}} = {\ frac {\ rho C_ {0} ^ {2}} {2s ^ {4} (1- \ chi)}} {\ biggl [} e {\ frac {s} {(1-s \ chi) ^ {2}}} {\ Bigl (} - \ _ gama {0} ^ {2} (1- \ chi) (1-s \ chi) + \ _ gama {0} [s \ {4 (\ qui -1) \ qui-2 \ 3 chi \} - 1] \\ & - \ exp (\ _ gama {0} \ chi) [\ _ gama {0} (\ qui -1) -1] (1-s \ chi) ^ {2} (\ _ gama {0} -3S) + s [3- \ qui s \ {(\ qui -2) s + 4 \}] {\ BIGR)} \\ & - \ exp \ esquerda [- {\ tfrac {\ _ gama {0}}}} {s (1-s \ chi) \ direito] [\ _ gama {0} (\ qui -1) -1] (\ _ gama {0} ^ {2} -4 \ _ gama {0} s + 2s ^ { 2}) ({\ texto {Ei}} [{\ tfrac {\ Gamma _ {0}} {s}} (1-s \ chi)] - {\ texto {Ei}} [{\ tfrac {\ Gamma _ {0}}}} {s]) {\ biggr]} \,. \ final {alinhados}}}$

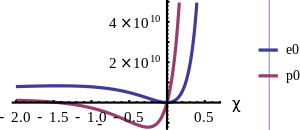
A parcela de e ₀ e p ₀ para o cobre como uma função de χ.

Para problemas de compressão comumente encontradas, uma aproximação para a solução exata é uma solução em série de potências da forma

${\ Displaystyle e_ {0} (V) = A + B \ chi (V) + C \ chi ^ {2} (V) + D \ chi ^ {3} (V) + \} pontos$

e

${\ Displaystyle P_ {0} (V) = - {\ frac {de_ {0}} {dV}} = - {\ frac {de_ {0}} {d \ qui}} \, {\ frac {d \ chi} {dV}} = {\ frac {1} {V_ {0}}} \, (2C \ B + chi + 3D \ chi ^ {2} + \ dots) \ ,.}$

Substituição no modelo Gruneisen nos dá a equação Mie-Gruneisen de Estado

${\ Displaystyle p = {\ frac {1} {V_ {0}}} \, (2C \ B + chi + 3D \ chi ^ {2} + \ dots) + {\ frac {\ Gamma _ {0}} {V_ {0}}} \ esquerda [e- (A + B \ qui + C \ chi ^ {2} + D \ chi ^ {3} + \ dots) \ direita] \ ,.}$

Se partirmos do princípio de que a energia interna e ₀ = 0 quando V = ₀ (χ = 0) que tem Um = 0. De modo semelhante, se assumirmos p ₀ = 0 quando V = V ₀ temos B = 0. O Mie- equação Gruneisen de estado pode então ser escrito como

${\ Displaystyle p = {\ frac {1} {V_ {0}}} \ esquerda [2C \ qui \ esquerda (1 - {\ tfrac {\ Gamma _ {0}} {2}} \ qui \ direita) + 3D \ chi ^ {2} \ esquerda (1 - {\ tfrac {\ _ gama {0}} {3}} \ qui \ direita) + \ dots \ direita] + \ _ gama {0}} E$

onde E é a energia interna por unidade de volume de referência. Várias formas desta equação de estado são possíveis.

Comparação da equação exata e de primeira ordem Mie-Gruneisen de Estado para o cobre.

Se tomarmos o termo de primeira ordem e substituí-lo na equação (2), podemos resolver para C para obter

${\ Displaystyle C = {\ frac {\ rho C_ {0} ^ {2} V_ {0}} {2 (1-s \ chi) ^ {2}}} \ ,.}$

Então, temos a seguinte expressão para p  :

${\ Displaystyle p = {\ frac {\ rho C_ {0} ^ {2} \ qui} {(1-s \ chi) ^ {2}}} \ esquerda (1 - {\ tfrac {\ Gamma _ {0 }} {2}} \ qui \ direita) + \ _ gama {0} E \ ,.}$

Esta é a primeira ordem comumente usado equação Mie-Gruneisen de Estado.

Veja também

• Impacto (mecânica)
• Onda de choque
• Choque (mecânica)
• tubo de choque
• choque hidrostática
• Alegra
• viscoplasticidade

Referências