Teorema do eleitor mediano - Median voter theorem

O teorema do eleitor mediano é uma proposição relacionada à votação por preferência classificada apresentada por Duncan Black em 1948. Ele afirma que se os eleitores e as políticas são distribuídos ao longo de um espectro unidimensional , com os eleitores classificando as alternativas em ordem de proximidade, então qualquer método de votação que satisfaz o critério de Condorcet elegerá o candidato mais próximo do eleitor mediano. Em particular, uma votação majoritária entre duas opções fará isso.

O teorema está associado à economia da escolha pública e à ciência política estatística . Partha Dasgupta e Eric Maskin argumentaram que ele fornece uma justificativa poderosa para métodos de votação baseados no critério de Condorcet. O teorema do equilíbrio da regra da maioria de Plott estende isso a duas dimensões.

Uma afirmação vagamente relacionada foi feita antes (em 1929) por Harold Hotelling . Não é um verdadeiro teorema e é mais propriamente conhecido como o eleitor mediano teoria ou eleitor mediano modelo . Diz que em uma democracia representativa , os políticos convergirão para o ponto de vista do eleitor mediano.

Declaração e prova do teorema

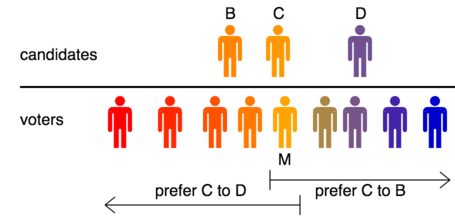
Candidato C   é o mais próximo mediana eleitor M .

Suponha que haja um número ímpar de eleitores e pelo menos dois candidatos, e suponha que as opiniões estejam distribuídas ao longo de um espectro. Suponha que cada eleitor classifique os candidatos em uma ordem de proximidade de forma que o candidato mais próximo do eleitor receba sua primeira preferência, o próximo mais próximo receba sua segunda preferência e assim por diante. Aí vem o eleitor mediano e vamos mostrar que a eleição será ganha pelo candidato mais próximo dele.

Prova . Deixe o eleitor mediano ser Marlene. O candidato mais próximo dela receberá seu primeiro voto de preferência. Suponha que esse candidato seja Charles e que ele esteja à esquerda dela. Então Marlene e todos os eleitores à sua esquerda (compreendendo a maioria do eleitorado) irão preferir Charles a todos os candidatos à sua direita, e Marlene e todos os eleitores à sua direita irão preferir Charles a todos os candidatos à sua esquerda.

O critério de Condorcet é definido como sendo satisfeito por qualquer método de votação que garanta que um candidato que é preferido a todos os outros candidatos pela maioria do eleitorado será o vencedor, e este é precisamente o caso de Charles aqui; portanto, Charles ganhará qualquer eleição conduzida usando um método que satisfaça o critério de Condorcet.

Portanto, em qualquer método de votação que satisfaça o critério de Condorcet, o vencedor será o candidato preferido pelo eleitor mediano. Para decisões binárias, o voto da maioria satisfaz o critério; para votos múltiplos, vários métodos o satisfazem (consulte o método de Condorcet ).

Premissas

O teorema também se aplica quando o número de eleitores é par, mas os detalhes dependem de como os empates são resolvidos.

A suposição de que as preferências são lançadas em ordem de proximidade pode ser relaxada para dizer apenas que elas têm um único pico .

A suposição de que as opiniões estão ao longo de uma linha real pode ser relaxada para permitir topologias mais gerais.

História

O teorema foi estabelecido pela primeira vez por Duncan Black em 1948. Ele escreveu que viu uma grande lacuna na teoria econômica sobre como o voto determina o resultado das decisões, incluindo decisões políticas. O artigo de Black desencadeou pesquisas sobre como a economia pode explicar os sistemas de votação. Em 1957, Anthony Downs expôs o teorema do eleitor mediano em seu livro Uma Teoria Econômica da Democracia .

Extensão para distribuições em mais de uma dimensão

O teorema do eleitor mediano em duas dimensões

O teorema do eleitor mediano se aplica de forma restrita às distribuições das opiniões dos eleitores em espaços de qualquer dimensão. Uma distribuição em mais de uma dimensão não tem necessariamente uma mediana em todas as direções (que pode ser denominada 'mediana omnidirecional'); no entanto, uma ampla classe de distribuições rotacionalmente simétricas, incluindo o Gaussian , que tem uma média deste tipo. Sempre que a distribuição dos eleitores tem uma mediana única em todas as direções, e os eleitores classificam os candidatos em ordem de proximidade, o teorema do eleitor mediano se aplica: o candidato mais próximo da mediana terá uma preferência majoritária sobre todos os seus rivais e será eleito por qualquer método de votação que satisfaça o critério de Condorcet. (A exclusividade aqui generaliza a propriedade garantida pela estranheza do tamanho da amostra em uma única dimensão.)

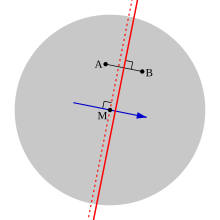
Prova . Veja o diagrama, no qual o disco cinza representa a distribuição do eleitor como uniforme em um círculo e M é a mediana em todas as direções. Sejam A e B dois candidatos, dos quais A é o mais próximo da mediana. Então, os eleitores que classificam A acima de B são precisamente os que estão à esquerda (isto é, o lado 'A') da linha vermelha sólida; e como A está mais próximo do que B de M, a mediana também está à esquerda desta linha.

Uma distribuição sem mediana em todas as direções

Agora, como M é uma mediana em todas as direções, ela coincide com a mediana unidimensional no caso particular da direção mostrada pela seta azul, que é perpendicular à linha vermelha sólida. Assim, se traçarmos uma linha vermelha quebrada através de M, perpendicular à seta azul, podemos dizer que metade dos eleitores está à esquerda dessa linha. Mas como essa linha está à esquerda da linha vermelha sólida, segue-se que mais da metade dos eleitores terão classificação A acima de B.

É fácil construir distribuições de eleitores que não tenham uma mediana em todas as direções. O exemplo mais simples consiste em uma distribuição limitada a 3 pontos que não se encontram em uma linha reta, como 1, 2 e 3 no segundo diagrama. Cada localização do eleitor coincide com a mediana sob um certo conjunto de projeções unidimensionais. Se A, B e C forem os candidatos, então '1' votará ABC, '2' votará BCA e '3' votará CAB, dando um ciclo de Condorcet. Este é o assunto do teorema de McKelvey – Schofield .

Relação entre a mediana em todas as direções e a mediana geométrica

Sempre que existe uma mediana omnidirecional única, ela determina o resultado dos métodos de votação de Condorcet. Ao mesmo tempo, a mediana geométrica pode ser identificada como o vencedor ideal de uma eleição de preferência por classificação (ver Comparação de sistemas eleitorais ). Portanto, é importante saber a relação entre os dois. Na verdade, sempre que existe uma mediana em todas as direções (pelo menos no caso de distribuições discretas), ela coincide com a mediana geométrica.

Diagrama para o lema

Lemma . Sempre que uma distribuição discreta tem uma mediana M   em todas as direções, os pontos de dados não localizados em M   devem vir em pares equilibrados ( A , A  ') em ambos os lados de M   com a propriedade de que A  -  M  -  A  ' é uma linha reta ( isto é. não como um  0  -  M  -  a  2 no diagrama).

Prova . Este resultado foi provado algebricamente por Charles Plott em 1967. Aqui damos uma prova geométrica simples por contradição em duas dimensões.

Suponha, ao contrário, que haja um conjunto de pontos A i que têm M   como mediana em todas as direções, mas para os quais os pontos não coincidentes com M   não vêm em pares equilibrados. Então, podemos remover deste conjunto quaisquer pontos em M , e quaisquer pares balanceados em torno de M , sem que M   deixe de ser uma mediana em qualquer direção; então M   permanece uma mediana omnidirecional.

Se o número de pontos restantes é ímpar, então podemos facilmente desenhar uma linha através de M   tal que a maioria dos pontos de mentir sobre um dos lados, contradizendo a propriedade mediana de M .

Se o número for par, digamos 2 n , então podemos rotular os pontos A  0 , A 1 , ... no sentido horário sobre M   começando em qualquer ponto (consulte o diagrama). Seja θ o ângulo subtendido pelo arco de M  - A  0 a M  - A n . Então, se θ <180 ° como mostrado, podemos traçar uma linha semelhante à linha vermelha quebrada através de M,   que tem a maioria dos pontos de dados em um lado dela, novamente contradizendo a propriedade mediana de M  ; enquanto que se θ> 180 ° o mesmo se aplica à maioria dos pontos do outro lado. E se θ = 180 °, então A  0 e A n formam um par balanceado, contradizendo outra suposição.    

Teorema . Sempre que uma distribuição discreta tem uma mediana M   em todas as direções, ela coincide com sua mediana geométrica.

Prova . A soma das distâncias de qualquer ponto P   a um conjunto de pontos de dados em pares balanceados ( A , A  ') é a soma dos comprimentos A  -  P  -  A  '. Cada comprimento individual desta forma é minimizado através P   quando a linha é linear, como acontece quando P   coincide com M . A soma das distâncias de P   a quaisquer pontos de dados localizados em M   é igualmente minimizada quando P   e M   coincidem. Assim, a soma das distâncias dos pontos de dados para P   é minimizada quando P   coincide com M  .

Lei de Hotelling

A afirmação mais informal - o modelo do eleitor mediano - está relacionada ao "princípio da diferenciação mínima" de Harold Hotelling , também conhecido como " lei de Hotelling ". Afirma que os políticos gravitam em torno da posição ocupada pelo eleitor mediano, ou mais geralmente em torno da posição favorecida pelo sistema eleitoral. Foi apresentado pela primeira vez (como uma observação, sem qualquer pretensão de rigor) por Hotelling em 1929.

Hotelling viu o comportamento dos políticos pelos olhos de um economista. Ele ficou impressionado com o fato de que as lojas que vendem um determinado produto muitas vezes se congregam na mesma parte da cidade, e viu isso como uma convergência de partidos políticos análogos. Em ambos os casos, pode ser uma política racional para maximizar a participação no mercado .

Como acontece com qualquer caracterização da motivação humana, ela depende de fatores psicológicos que não são facilmente previsíveis e estão sujeitos a muitas exceções. Também depende do sistema de votação: os políticos não convergirão para o eleitor mediano a menos que o processo eleitoral o faça. Se um processo eleitoral dá mais peso aos eleitores rurais do que aos urbanos, então os partidos tendem a convergir para políticas que favorecem as áreas rurais em vez da verdadeira mediana.

Usos do teorema do eleitor mediano

O teorema é valioso pela luz que lança sobre a otimização (e os limites da otimização) de certos sistemas de votação.

Valerio Dotti aponta áreas mais amplas de aplicação:

O Teorema do Eleitor Mediano provou ser extremamente popular na literatura de Economia Política. A principal razão é que ele pode ser adotado para derivar implicações testáveis ​​sobre a relação entre algumas características da população eleitoral e o resultado da política, abstraindo de outras características do processo político.

Ele acrescenta que ...

O resultado do eleitor mediano foi aplicado a uma variedade incrível de perguntas. Exemplos são a análise da relação entre a desigualdade de renda e o tamanho da intervenção governamental nas políticas redistributivas (Meltzer e Richard, 1981), o estudo dos determinantes das políticas de imigração (Razin e Sadka, 1999), a extensão da tributação sobre os diferentes vínculos de renda (Bassetto e Benhabib, 2006) e muitos mais.

Veja também

Referências

Leitura adicional

Link externo