Amostragem de transformação inversa - Inverse transform sampling

Transformada inversa de amostragem (também conhecido como amostragem inversão , a transformação integral de probabilidade inversa , o método de transformação inversa , Smirnov transformar , ou a regra de ouro ) é um método básico para a amostragem de números pseudo-aleatórios , ou seja, para a geração de números de amostra em aleatória a partir de qualquer distribuição de probabilidade dada sua função de distribuição cumulativa .

A amostragem de transformação inversa pega amostras uniformes de um número entre 0 e 1, interpretado como uma probabilidade, e então retorna o maior número do domínio da distribuição tal que . Por exemplo, imagine que é a distribuição normal padrão com média zero e desvio padrão um. A tabela abaixo mostra amostras retiradas da distribuição uniforme e sua representação na distribuição normal padrão. ${\ displaystyle u}$ ${\ displaystyle x}$ ${\ displaystyle P (X)}$ ${\ displaystyle P (- \ infty <X <x) \ leq u}$ ${\ displaystyle P (X)}$

Transformação de amostra uniforme para normal
${\ displaystyle u}$	${\ displaystyle F ^ {- 1} (u)}$
0,5	0
0,975	1,95996
0,995	2,5758
0,999999	4,75342
1-2 ^-52	8,12589

Amostragem de transformação inversa para distribuição normal

Estamos escolhendo aleatoriamente uma proporção da área sob a curva e retornando o número no domínio de forma que exatamente essa proporção da área ocorra à esquerda desse número. Intuitivamente, é improvável que escolhamos um número na extremidade da cauda porque há muito pouca área nelas que exigiria a escolha de um número muito próximo de zero ou um.

Computacionalmente, este método envolve o cálculo da função de quantil da distribuição - em outras palavras, o cálculo da função de distribuição cumulativa (CDF) da distribuição (que mapeia um número no domínio a uma probabilidade entre 0 e 1) e, em seguida, a inversão dessa função. Essa é a fonte do termo "inverso" ou "inversão" na maioria dos nomes para esse método. Observe que, para uma distribuição discreta , calcular o CDF em geral não é muito difícil: simplesmente somamos as probabilidades individuais para os vários pontos da distribuição. Para uma distribuição contínua , no entanto, precisamos integrar a função de densidade de probabilidade (PDF) da distribuição, o que é impossível de fazer analiticamente para a maioria das distribuições (incluindo a distribuição normal ). Como resultado, este método pode ser computacionalmente ineficiente para muitas distribuições e outros métodos são preferidos; no entanto, é um método útil para a construção de amostradores de aplicação mais geral, como aqueles baseados em amostragem de rejeição .

Para a distribuição normal , a falta de uma expressão analítica para a função de quantil correspondente significa que outros métodos (por exemplo, a transformação de Box-Muller ) podem ser preferidos computacionalmente. É comum que, mesmo para distribuições simples, o método de amostragem por transformação inversa possa ser aprimorado: consulte, por exemplo, o algoritmo zigurate e a amostragem de rejeição . Por outro lado, é possível aproximar a função de quantil da distribuição normal com extrema precisão usando polinômios de grau moderado e, de fato, o método para fazer isso é rápido o suficiente para que a amostragem por inversão seja agora o método padrão para amostragem de uma distribuição normal no pacote estatístico R .

Definição

A transformação integral de probabilidade afirma que se for uma variável aleatória contínua com função de distribuição cumulativa , então a variável aleatória tem uma distribuição uniforme em [0, 1]. A transformação integral de probabilidade inversa é apenas o inverso disso: especificamente, se tem uma distribuição uniforme em [0, 1] e se tem uma distribuição cumulativa , então a variável aleatória tem a mesma distribuição que . ${\ displaystyle X}$ ${\ displaystyle F_ {X}}$ ${\ displaystyle Y = F_ {X} (X)}$ ${\ displaystyle Y}$ ${\ displaystyle X}$ ${\ displaystyle F_ {X}}$ ${\ displaystyle F_ {X} ^ {- 1} (Y)}$ ${\ displaystyle X}$

Gráfico da técnica de inversão de a . No canto inferior direito vemos a função regular e no canto superior esquerdo sua inversão.

{\ displaystyle x}

{\ displaystyle F (x)}

Intuição

De , queremos gerar com CDF . Assumimos ser uma função estritamente crescente, que fornece boa intuição. ${\ displaystyle U \ sim \ mathrm {Unif} [0,1]}$ ${\ displaystyle X}$ ${\ displaystyle F_ {X} (x).}$ ${\ displaystyle F_ {X} (x)}$

Queremos ver se podemos encontrar alguma transformação estritamente monótona , como essa . Nós teremos ${\ displaystyle T: [0,1] \ mapsto \ mathbb {R}}$ ${\ displaystyle T (U) {\ overset {d} {=}} X}$

${\ displaystyle F_ {X} (x) = \ Pr (X \ leq x) = \ Pr (T (U) \ leq x) = \ Pr (U \ leq T ^ {- 1} (x)) = T ^ {- 1} (x), {\ text {for}} x \ in \ mathbb {R},}$

onde a última etapa usada é quando é uniforme . ${\ displaystyle \ Pr (U \ leq y) = y}$ ${\ displaystyle U}$ ${\ displaystyle (0,1)}$

Então, temos que ser a função inversa de , ou, equivalentemente ${\ displaystyle F_ {X}}$ ${\ displaystyle T}$ ${\ displaystyle T (u) = F_ {X} ^ {- 1} (u), u \ in [0,1].}$

Portanto, podemos gerar a partir de ${\ displaystyle X}$ ${\ displaystyle F_ {X} ^ {- 1} (U).}$

O método

Esquema da amostragem por transformada inversa. A função inversa de pode ser definida por .

{\ displaystyle y = F_ {X} (x)}

{\ displaystyle F_ {X} ^ {- 1} (y) = \ mathrm {inf} \ {x | F_ {X} (x) \ geq y \}}

Uma animação de como a amostragem de transformação inversa gera valores aleatórios normalmente distribuídos a partir de valores aleatórios uniformemente distribuídos

O problema que o método de amostragem por transformação inversa resolve é o seguinte:

Let Ser uma variável aleatória cuja distribuição pode ser descrita pela função de distribuição cumulativa . ${\ displaystyle X}$ ${\ displaystyle F_ {X}}$
Queremos gerar valores que são distribuídos de acordo com esta distribuição. ${\ displaystyle X}$

O método de amostragem de transformação inversa funciona da seguinte forma:

Gere um número aleatório a partir da distribuição uniforme padrão no intervalo , por exemplo, de ${\ displaystyle u}$ ${\ displaystyle [0,1]}$ ${\ displaystyle U \ sim \ mathrm {Unif} [0,1].}$
Encontre o inverso do CDF desejado, por exemplo . ${\ displaystyle F_ {X} ^ {- 1} (x)}$
Compute . A variável aleatória calculada tem distribuição . ${\ displaystyle X = F_ {X} ^ {- 1} (u)}$ ${\ displaystyle X}$ ${\ displaystyle F_ {X} (x)}$

Expresso de forma diferente, dada uma variável uniforme contínua em e uma função de distribuição cumulativa invertível , a variável aleatória tem distribuição (ou, é distribuída ). ${\ displaystyle U}$ ${\ displaystyle [0,1]}$ ${\ displaystyle F_ {X}}$ ${\ displaystyle X = F_ {X} ^ {- 1} (U)}$ ${\ displaystyle F_ {X}}$ ${\ displaystyle X}$ ${\ displaystyle F_ {X}}$

Um tratamento de tais funções inversas como objetos que satisfazem equações diferenciais pode ser dado. Algumas dessas equações diferenciais admitem soluções de séries de potências explícitas, apesar de sua não linearidade.

Exemplos

Por exemplo, suponha que temos uma variável aleatória e uma função de distribuição cumulativa ${\ displaystyle U \ sim \ mathrm {Unif} (0,1)}$

{\ displaystyle {\ begin {alinhado} F (x) = 1- \ exp (- {\ sqrt {x}}) \ end {alinhado}}}

Para realizar uma inversão, queremos resolver para

{\ displaystyle F (F ^ {- 1} (u)) = u}

{\ displaystyle {\ begin {alinhados} F (F ^ {- 1} (u)) & = u \\ 1- \ exp \ left (- {\ sqrt {F ^ {- 1} (u)}} \ direita) & = u \\ F ^ {- 1} (u) & = (- \ log (1-u)) ^ {2} \\ & = (\ log (1-u)) ^ {2} \ fim {alinhado}}}

A partir daqui, executaríamos as etapas um, dois e três.

Como outro exemplo, usamos a distribuição exponencial com para x ≥ 0 (e 0 caso contrário). Resolvendo y = F (x), obtemos a função inversa ${\ displaystyle F_ {X} (x) = 1-e ^ {- \ lambda x}}$

{\ displaystyle x = F ^ {- 1} (y) = - {\ frac {1} {\ lambda}} \ ln (1-y).}

Significa que, se extrairmos algum de ae calcularmos, isso tem distribuição exponencial.

{\ displaystyle y_ {0}}

{\ displaystyle U \ sim \ mathrm {Unif} (0,1)}

{\ displaystyle x_ {0} = F_ {X} ^ {- 1} (y_ {0}) = - {\ frac {1} {\ lambda}} \ ln (1-y_ {0}),}

{\ displaystyle x_ {0}}

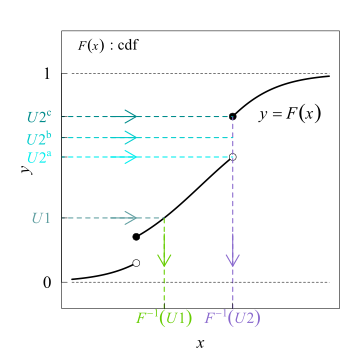
A ideia é ilustrada no gráfico a seguir:

Os números aleatórios y _i são gerados a partir de uma distribuição uniforme entre 0 e 1, ou seja, Y ~ U (0, 1). Eles são esboçados como pontos coloridos no eixo y. Cada um dos pontos é mapeado de acordo com x = F ⁻¹ (y), que é mostrado com setas cinza para dois pontos de exemplo. Neste exemplo, usamos uma distribuição exponencial. Portanto, para x ≥ 0, a densidade de probabilidade é e a função de distribuição cumulativa é . Portanto ,. Podemos ver que usando este método, muitos pontos acabam perto de 0 e apenas alguns pontos acabam tendo valores de x altos - exatamente como é esperado para uma distribuição exponencial.

{\ displaystyle \ varrho _ {X} (x) = \ lambda e ^ {- \ lambda \, x}}

{\ displaystyle F (x) = 1-e ^ {- \ lambda \, x}}

{\ displaystyle x = F ^ {- 1} (y) = - {\ frac {\ ln (1-y)} {\ lambda}}}

Observe que a distribuição não muda se começarmos com 1-y em vez de y. Para fins computacionais, portanto, é suficiente gerar números aleatórios y em [0, 1] e, em seguida, simplesmente calcular

{\ displaystyle x = F ^ {- 1} (y) = - {\ frac {1} {\ lambda}} \ ln (y).}

Prova de correção

Seja F uma função de distribuição cumulativa contínua , e seja F ^-1 sua função inversa (usando o ínfimo porque os CDFs são fracamente monotônicos e contínuos à direita ):

{\ displaystyle F ^ {- 1} (u) = \ inf \; \ {x \ mid F (x) \ geq u \} \ qquad (0 <u <1).}

Afirmação: Se U é uma variável aleatória uniforme em (0, 1), então tem F como seu CDF. ${\ displaystyle F ^ {- 1} (U)}$

Prova:

{\ displaystyle {\ begin {alinhados} & \ Pr (F ^ {- 1} (U) \ leq x) \\ & {} = \ Pr (U \ leq F (x)) \ quad & ({\ text {aplicando}} F, {\ text {a ambos os lados}}) \\ & {} = F (x) \ quad & ({\ text {porque}} \ Pr (U \ leq y) = y, {\ texto {quando U é uniforme em}} (0,1)) \\\ end {alinhado}}}

Distribuição truncada

A amostragem de transformação inversa pode ser simplesmente estendida a casos de distribuições truncadas no intervalo sem o custo de amostragem de rejeição: o mesmo algoritmo pode ser seguido, mas em vez de gerar um número aleatório uniformemente distribuído entre 0 e 1, gerar uniformemente distribuído entre e , e em seguida, pegue novamente . ${\ displaystyle (a, b]}$ ${\ displaystyle u}$ ${\ displaystyle u}$ ${\ displaystyle F (a)}$ ${\ displaystyle F (b)}$ ${\ displaystyle F ^ {- 1} (u)}$

Redução do número de inversões

Para obter um grande número de amostras, é necessário realizar o mesmo número de inversões da distribuição. Uma forma possível de reduzir o número de inversões ao obter um grande número de amostras é a aplicação do chamado amostrador Stochastic Collocation Monte Carlo (amostrador SCMC) dentro de uma estrutura de expansão do caos polinomial . Isso nos permite gerar qualquer número de amostras de Monte Carlo com apenas algumas inversões da distribuição original com amostras independentes de uma variável para a qual as inversões estão analiticamente disponíveis, por exemplo, a variável normal padrão.

Veja também

Transformada integral de probabilidade
Copula , definido por meio da transformada integral de probabilidade.
Função quantílica , para a construção explícita de CDFs inversos.
Função de distribuição inversa para uma definição matemática precisa de distribuições com componentes discretos.

Referências

^ Universidade de Aalto, N. Hyvönen, métodos computacionais em problemas inversos. Décima segunda palestra https://noppa.tkk.fi/noppa/kurssi/mat-1.3626/luennot/Mat-1_3626_lecture12.pdf
^ Luc Devroye (1986). Geração de variável aleatória não uniforme (PDF) . Nova York: Springer-Verlag.
^ https://stat.ethz.ch/R-manual/R-devel/library/base/html/Random.html
^ Steinbrecher, G., Shaw, WT (2008). Mecânica quântica. European Journal of Applied Mathematics 19 (2): 87-112.
^ Luc Devroye (1986). "Seção 2.2. Inversão por solução numérica de F ( X ) = U " (PDF) . Geração de variável aleatória não uniforme . Nova York: Springer-Verlag.
^ LA Grzelak, JAS Witteveen, M. Suarez e CW Oosterlee. Amostrador de Monte Carlo de colocação estocástica: Amostragem altamente eficiente de distribuições “caras”. https://ssrn.com/abstract=2529691

[aalto-1] Universidade de Aalto, N. Hyvönen, métodos computacionais em problemas inversos. Décima segunda palestra https://noppa.tkk.fi/noppa/kurssi/mat-1.3626/luennot/Mat-1_3626_lecture12.pdf

[2] Luc Devroye (1986). Geração de variável aleatória não uniforme (PDF) . Nova York: Springer-Verlag.

[3] ttps://stat.ethz.ch/R-manual/R-devel/library/base/html/Random.html

[4] Steinbrecher, G., Shaw, WT (2008). Mecânica quântica. European Journal of Applied Mathematics 19 (2): 87-112.

[5] Luc Devroye (1986). "Seção 2.2. Inversão por solução numérica de F ( X ) = U " (PDF) . Geração de variável aleatória não uniforme . Nova York: Springer-Verlag.

[6] LA Grzelak, JAS Witteveen, M. Suarez e CW Oosterlee. Amostrador de Monte Carlo de colocação estocástica: Amostragem altamente eficiente de distribuições “caras”. https://ssrn.com/abstract=2529691

Languages

In other projects