Krigagem com gradiente aprimorado - Gradient-enhanced kriging

A krigagem aprimorada por gradiente ( GEK ) é uma técnica de modelagem substituta usada em engenharia. Um modelo substituto (alternativamente conhecido como metamodelo , superfície de resposta ou emulador) é uma previsão da saída de um código de computador caro. Essa previsão é baseada em um pequeno número de avaliações do caro código de computador.

Introdução

Exemplo de dados unidimensionais interpolados por Kriging e GEK. A linha preta indica a função de teste, enquanto os círculos cinza indicam 'observações', 'amostras' ou 'avaliações' da função de teste. A linha azul é a média da Krigagem, a área sombreada em azul ilustra o desvio padrão da Krigagem. Com GEK podemos adicionar as informações do gradiente, ilustradas em vermelho, o que aumenta a precisão da previsão.

Solucionadores adjuntos estão agora se tornando disponíveis em uma variedade de solucionadores de dinâmica de fluidos computacional (CFD), como Fluent , OpenFOAM , SU2 e US3D. Desenvolvidos originalmente para otimização , os solucionadores adjuntos estão agora encontrando cada vez mais uso na quantificação de incertezas .

Aceleração linear

Um solucionador adjunto permite calcular o gradiente da quantidade de interesse em relação a todos os parâmetros de projeto ao custo de uma solução adicional. Isso, potencialmente, leva a um aumento de velocidade linear : o custo computacional de construir uma redução substituta precisa e o aumento de velocidade computacional resultante é dimensionado linearmente com o número de parâmetros de projeto. ${\ displaystyle s}$ ${\ displaystyle d}$

O raciocínio por trás dessa aceleração linear é direto. Suponha que executamos soluções primárias e soluções adjuntas, a um custo total de . Isso resulta em dados; valores para a quantidade de interesse e derivadas parciais em cada um dos gradientes. Agora suponha que cada derivada parcial forneça tanta informação para nosso substituto quanto uma única solução primal. Então, o custo total para obter a mesma quantidade de informações de soluções primárias é apenas . A aceleração é a proporção desses custos: ${\ displaystyle N}$ ${\ displaystyle N}$ ${\ displaystyle 2N}$ ${\ displaystyle N + dN}$ ${\ displaystyle N}$ ${\ displaystyle d}$ ${\ displaystyle N}$ ${\ displaystyle N + dN}$

{\ displaystyle s = {\ frac {N + dN} {2N}} = {\ frac {1} {2}} + {\ frac {1} {2}} d.}

Um speedup linear foi demonstrado para um problema de interação fluido-estrutura e para um aerofólio transônico .

Barulho

Um problema com gradientes baseados em adjuntos em CFD é que eles podem ser particularmente barulhentos . Quando derivado em uma estrutura Bayesiana , GEK permite incorporar não apenas a informação do gradiente, mas também a incerteza nessa informação do gradiente.

Abordagem

Ao usar GEK, deve-se seguir os seguintes passos:

Criar um projeto de experimento (DoE): O DoE ou 'plano de amostragem' é uma lista de diferentes locais no espaço do projeto. O DoE indica quais combinações de parâmetros serão usadas para amostrar a simulação de computador. Com Kriging e GEK, uma escolha comum é usar um projeto Latin Hypercube Design (LHS) com um critério 'maximin'. O design LHS está disponível em códigos de script como MATLAB ou Python .
Faça observações: para cada amostra em nosso DoE, executa-se a simulação de computador para obter a Quantidade de Interesse (QoI).
Construir o substituto: Um usa as equações do preditor GEK para construir o substituto condicional nas observações obtidas.

Uma vez que o substituto foi construído, ele pode ser usado de diferentes maneiras, por exemplo, para quantificação de incerteza baseada em substituto (UQ) ou otimização .

Equações preditivas

Em uma estrutura Bayesiana , usamos o Teorema de Bayes para prever a média da Krigagem e a covariância condicional às observações. Ao usar GEK, as observações geralmente são os resultados de várias simulações de computador. GEK pode ser interpretado como uma forma de regressão do processo gaussiano .

Kriging

Ao longo das linhas de, estamos interessados na saída de nossa simulação de computador, para a qual assumimos a distribuição de probabilidade anterior normal : ${\ displaystyle X}$

{\ displaystyle X \ sim {\ mathcal {N}} (\ mu, P),}

com média anterior e matriz de covariância anterior . As observações têm a probabilidade normal : ${\ displaystyle \ mu}$ ${\ displaystyle P}$ ${\ displaystyle y}$

{\ displaystyle Y \ mid x \ sim {\ mathcal {N}} (Hx, R),}

com a matriz de observação e a matriz de covariância do erro de observação, que contém as incertezas da observação . Depois de aplicar o Teorema de Bayes , obtemos uma distribuição de probabilidade posterior normalmente distribuída , com média de Krigagem: ${\ displaystyle H}$ ${\ displaystyle R}$

{\ displaystyle \ operatorname {E} (X \ mid y) = \ mu + K (yH \ mu),}

e covariância de Krigagem:

{\ displaystyle \ operatorname {cov} (X \ mid y) = (I-KH) P,}

onde temos a matriz de ganho:

{\ displaystyle K = PH ^ {T} (R + HPH ^ {T}) ^ {- 1}.}

Na Krigagem, a matriz de covariância anterior é gerada a partir de uma função de covariância. Um exemplo de função de covariância é a covariância Gaussiana: ${\ displaystyle P}$

{\ displaystyle P_ {ij} = \ sigma ^ {2} \ exp \ left (- \ sum _ {k} {\ frac {| \ xi _ {jk} - \ xi _ {ik} | ^ {2}} {2 \ theta _ {k} ^ {2}}} \ right),}

onde somamos as dimensões e são os parâmetros de entrada. Os hiperparâmetros , e pode ser estimado a partir de um Maximum Likelihood Estimado (MLE). ${\ displaystyle k}$ ${\ displaystyle \ xi}$ ${\ displaystyle \ mu}$ ${\ displaystyle \ sigma}$ ${\ displaystyle \ theta}$

GEK indireto

Existem várias maneiras de implementar GEK. O primeiro método, GEK indireto, define um tamanho de passo pequeno, mas finito , e usa as informações do gradiente para anexar dados sintéticos às observações , consulte por exemplo. A Krigagem Indireta é sensível à escolha do tamanho do passo e não pode incluir incertezas de observação . ${\ displaystyle h}$ ${\ displaystyle y}$ ${\ displaystyle h}$

GEK direto (por meio da matriz de covariância anterior)

GEK direto é uma forma de co-Krigagem, onde adicionamos as informações do gradiente como covariáveis. Isso pode ser feito modificando a covariância anterior ou modificando a matriz de observação ; ambas as abordagens levam ao mesmo preditor GEK. Quando construímos GEK direto por meio da matriz de covariância anterior, acrescentamos as derivadas parciais e modificamos a matriz de covariância anterior de modo que ela também contenha as derivadas (e segundas derivadas) da função de covariância, consulte por exemplo. As principais vantagens do GEK direto sobre o GEK indireto são: 1) não temos que escolher um tamanho de etapa, 2) podemos incluir incertezas de observação para os gradientes em , e 3) é menos suscetível a mau condicionamento da matriz de ganho . ${\ displaystyle P}$ ${\ displaystyle H}$ ${\ displaystyle y}$ ${\ displaystyle P}$ ${\ displaystyle R}$ ${\ displaystyle K}$

GEK direto (por meio da matriz de observação)

Outra maneira de chegar ao mesmo preditor GEK direto é anexar as derivadas parciais às observações e incluir os operadores das derivadas parciais na matriz de observação , ver por exemplo. ${\ displaystyle y}$ ${\ displaystyle H}$

Krigagem aprimorada por gradiente para problemas dimensionais elevados (método indireto)

Os métodos atuais de krigagem aprimorada por gradiente não escalam bem com o número de pontos de amostragem devido ao rápido crescimento no tamanho da matriz de correlação, onde novas informações são adicionadas para cada ponto de amostragem em cada direção do espaço de projeto. Além disso, eles não escalam bem com o número de variáveis independentes devido ao aumento no número de hiperparâmetros que precisam ser estimados. Para resolver esse problema, foi desenvolvida uma nova abordagem de modelo substituto aprimorado por gradiente que reduziu drasticamente o número de hiperparâmetros por meio do uso do método de mínimos quadrados parciais que mantém a precisão. Além disso, esse método é capaz de controlar o tamanho da matriz de correlação adicionando apenas os pontos relevantes definidos por meio das informações fornecidas pelo método dos mínimos quadrados parciais. Para mais detalhes, veja. Essa abordagem é implementada no Surrogate Modeling Toolbox (SMT) em Python ( https://github.com/SMTorg/SMT ) e é executado em Linux, macOS e Windows. SMT é distribuído sob a nova licença BSD.

Krigagem aprimorada por gradiente aumentado (método direto)

Uma estrutura universal aumentada é proposta para anexar derivados de qualquer ordem às observações. Este método pode ser visto como uma generalização do Direct GEK que leva em consideração derivadas de ordem superior. Além disso, as observações e derivados não precisam ser medidos no mesmo local sob esta estrutura.

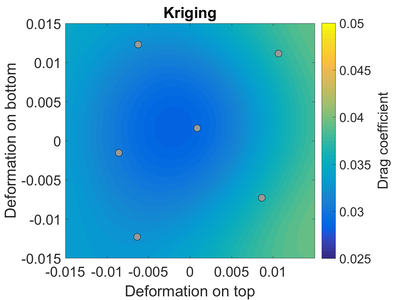
Exemplo: coeficiente de arrasto de um aerofólio transônico

Aerofólio transônico.

Resultados de referência para o coeficiente de arrasto de um aerofólio transônico, com base em um grande número de simulações CFD. Os eixos horizontal e vertical mostram a deformação da forma do aerofólio.

Modelo substituto de krigagem do coeficiente de arrasto de um aerofólio transônico. Os pontos cinza indicam as configurações para as quais o solucionador CFD foi executado.

Modelo substituto GEK do coeficiente de arrasto de um aerofólio transônico. Os pontos cinza indicam as configurações para as quais o solucionador CFD foi executado, as setas indicam os gradientes.

Como exemplo, considere o fluxo sobre um aerofólio transônico . O aerofólio está operando a um número Mach de 0,8 e um ângulo de ataque de 1,25 graus. Assumimos que a forma do aerofólio é incerta; as partes superior e inferior do aerofólio podem ter se deslocado para cima ou para baixo devido às tolerâncias de fabricação. Em outras palavras, a forma do aerofólio que estamos usando pode ser ligeiramente diferente do aerofólio que projetamos.

À direita, vemos os resultados de referência para o coeficiente de arrasto do aerofólio, com base em um grande número de simulações CFD. Observe que o arrasto mais baixo, que corresponde ao desempenho 'ótimo', está próximo ao projeto de 'linha de base' indeformado do aerofólio em (0,0).

Depois de projetar um plano de amostragem (indicado pelos pontos cinza) e executar o solucionador CFD nesses locais de amostra, obtemos o modelo substituto de Krigagem. O substituto da Kriging está perto da referência, mas talvez não tão perto quanto desejaríamos.

Na última figura, melhoramos a precisão desse modelo substituto incluindo as informações de gradiente baseadas em adjunto, indicadas pelas setas, e aplicando GEK.

Formulários

GEK encontrou os seguintes aplicativos:

1993: Problema de projeto para uma função-teste de modelo de poço.
2002: Projeto aerodinâmico de um jato executivo supersônico.
2008: Quantificação de incerteza para um aerofólio transônico com parâmetros de forma incertos.
2009: Quantificação de incerteza para um aerofólio transônico com parâmetros de forma incertos.
2012: Construção de um modelo substituto para um problema de divergência de painel, um problema de interação fluido-estrutura . Demonstração de uma aceleração linear.
2013: Quantificação de incerteza para um aerofólio transônico com ângulo de ataque incerto e número de Mach.
2014: Quantificação da incerteza para a simulação RANS de um aerofólio, com os parâmetros do modelo de turbulência k-épsilon como entradas incertas.
2015: Quantificação de incerteza para a simulação de Euler de um aerofólio transônico com parâmetros de forma incertos. Demonstração de uma aceleração linear.
2016: Construção do modelo substituto para dois problemas de interação fluido-estrutura .
2017: Grande revisão de modelos substitutos com gradiente aprimorado, incluindo muitos detalhes relacionados à krigagem com gradiente aprimorado.
2017: Propagação da incerteza para um sistema de energia nuclear.
2020: Otimização da geometria molecular.

Languages

In other projects