Teorema de rotação de Euler - Euler's rotation theorem

Em geometria , o teorema da rotação de Euler afirma que, no espaço tridimensional , qualquer deslocamento de um corpo rígido de forma que um ponto do corpo rígido permaneça fixo equivale a uma única rotação em torno de algum eixo que passa pelo ponto fixo . Isso também significa que a composição de duas rotações também é uma rotação. Portanto, o conjunto de rotações possui uma estrutura de grupo, conhecida como grupo de rotação .

O teorema tem o nome de Leonhard Euler , que o provou em 1775 por meio da geometria esférica . O eixo de rotação é conhecido como eixo de Euler , normalmente representado por um vetor unitário ê . Seu produto pelo ângulo de rotação é conhecido como vetor eixo-ângulo . A extensão do teorema à cinemática produz o conceito de eixo instantâneo de rotação , uma linha de pontos fixos.

Em termos de álgebra linear, o teorema afirma que, no espaço 3D, quaisquer dois sistemas de coordenadas cartesianas com uma origem comum são relacionados por uma rotação em torno de algum eixo fixo. Isso também significa que o produto de duas matrizes de rotação é novamente uma matriz de rotação e que para uma matriz de rotação de não identidade um valor próprio é 1 e os outros dois são ambos complexos, ou ambos iguais a −1. O autovetor correspondente a este autovalor é o eixo de rotação que conecta os dois sistemas.

Teorema de Euler (1776)

Euler afirma o teorema da seguinte forma:

Theorema. Quomodocunque sphaera circa centrum suum conuertatur, semper assignari potest diâmetro, cuius directio in situ translato conueniat cum situ initiali.

ou (em inglês):

Quando uma esfera é movida em torno de seu centro, é sempre possível encontrar um diâmetro cuja direção na posição deslocada é a mesma da posição inicial.

Prova

A prova original de Euler foi feita usando geometria esférica e, portanto, sempre que ele fala sobre triângulos, eles devem ser entendidos como triângulos esféricos .

Análise anterior

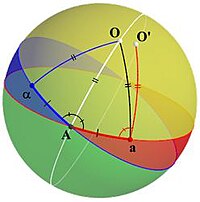
Para chegar a uma prova, Euler analisa como seria a situação se o teorema fosse verdadeiro. Para tanto, suponha que a linha amarela na Figura 1 passe pelo centro da esfera e seja o eixo de rotação que estamos procurando, e o ponto O é um dos dois pontos de interseção desse eixo com a esfera. Em seguida, ele considera um grande círculo arbitrário que não contém ó (o círculo azul), e a sua imagem depois da rotação (o círculo vermelho), que é um outro grande círculo não contendo ó . Ele rotula um ponto na sua intersecção como ponto A . (Se os círculos coincidem, então A pode ser considerado qualquer ponto em qualquer um; caso contrário, A é um dos dois pontos de intersecção.)

Agora A está no círculo inicial (o círculo azul), então sua imagem estará no círculo transportado (vermelho). Ele rotula essa imagem como ponto a . Como A também está no círculo transportado (vermelho), é a imagem de outro ponto que estava no círculo inicial (azul) e ele rotula essa pré-imagem como α (ver Figura 2 ). Em seguida, ele considera os dois arcos juntam α e um para um . Esses arcos têm o mesmo comprimento porque o arco αA está mapeado no arco Aa . Além disso, como O é um ponto fixo, o triângulo αOA é mapeado no triângulo AOa , então esses triângulos são isósceles e formam o ângulo AO dividida em duas partes ∠ αAa .

Construção do melhor ponto candidato

Vamos construir um ponto que pode ser invariante usando as considerações anteriores. Começamos com o grande círculo azul e sua imagem sob a transformação, que é o grande círculo vermelho como na Figura 1 . Seja o ponto A um ponto de intersecção desses círculos. Se uma imagem está sob a transformação é o mesmo ponto em seguida Um é um ponto fixo da transformação, e uma vez que o centro é também um ponto fixo, o diâmetro da esfera contendo Uma é o eixo de rotação e o teorema está provado.

Caso contrário, nós rotulamos A imagem ‘s como um e sua preimage como α , e ligar estes dois pontos para A com arcos αA e Aa . Esses arcos têm o mesmo comprimento. Construa o grande círculo que divide ∠ αAa ao meio e localize o ponto O nesse grande círculo de modo que os arcos AO e aO tenham o mesmo comprimento, e chame a região da esfera contendo O e delimitada pelos grandes círculos azul e vermelho o interior de ∠ αAa . (Ou seja, a região amarela na Figura 3. ) Então, como αA = Aa e O está na bissetriz de ∠ αAa , também temos αO = aO .

Prova de sua invariância sob a transformação

Agora vamos supor que O ' é a imagem de O . Então sabemos que ∠ αAO = ∠ AaO ′ e a orientação é preservada, então O ′ deve ser interior a ∠ αAa . Agora, AO é transformado em aO ′ , então AO = aO ′ . Visto que AO também tem o mesmo comprimento que aO , ∠ AaO = ∠ aAO . Mas ∠ AAO = ∠ AAO ' , de modo ∠ AAO = ∠ AAO' e, portanto, ó ' é o mesmo ponto que ó . Em outras palavras, O é um ponto fixo da transformação e, como o centro também é um ponto fixo, o diâmetro da esfera que contém O é o eixo de rotação.

Notas finais sobre a construção

Euler também aponta que O pode ser encontrado cruzando a bissetriz perpendicular de Aa com a bissetriz do ângulo de ∠ αAO , uma construção que pode ser mais fácil na prática. Ele também propôs a interseção de dois planos:

• o plano de simetria do ângulo ∠ αAa (que passa pelo centro C da esfera), e
• o plano de simetria do arco Aa (que também passa por C ).

Proposição . Esses dois planos se cruzam em um diâmetro. Este diâmetro é o que procuramos.

Prova . Vamos chamar de O qualquer um dos pontos finais (há dois) desse diâmetro sobre a superfície da esfera. Como αA é mapeado em Aa e os triângulos têm os mesmos ângulos, segue-se que o triângulo OαA é transportado para o triângulo OAa . Portanto, o ponto O deve permanecer fixo sob o movimento.

Corolários . Isso também mostra que a rotação da esfera pode ser vista como duas reflexões consecutivas sobre os dois planos descritos acima. Os pontos em um plano de espelho são invariantes sob reflexão e, portanto, os pontos em sua interseção (uma linha: o eixo de rotação) são invariantes sob ambos os reflexos e, portanto, sob a rotação.

Outra forma simples para encontrar o eixo de rotação é, considerando o plano no qual os pontos de ácido a , Um , uma mentira. O eixo de rotação é obviamente ortogonal a este plano e passa pelo centro C da esfera.

Dado que, para um corpo rígido, qualquer movimento que deixe um eixo invariante é uma rotação, isso também prova que qualquer composição arbitrária de rotações é equivalente a uma única rotação em torno de um novo eixo.

Prova de matriz

Uma rotação espacial é um mapa linear em correspondência de um-para-um com um 3 × 3 rotação matriz R que transforma uma coordenada vector X em X , que é Rx = X . Portanto, outra versão do teorema de Euler é que para cada rotação R , existe um vetor diferente de zero n para o qual Rn = n ; esta é exatamente a afirmação de que n é um autovetor de R associado ao autovalor 1. Portanto, é suficiente provar que 1 é um autovalor de R ; o eixo de rotação de R será a linha μ n , onde n é o autovetor com autovalor 1.

Uma matriz de rotação tem a propriedade fundamental de que seu inverso é sua transposta, ou seja,

${\ displaystyle \ mathbf {R} ^ {\ mathsf {T}} \ mathbf {R} = \ mathbf {R} \ mathbf {R} ^ {\ mathsf {T}} = \ mathbf {I},}$

onde I é a matriz de identidade 3 × 3 e o sobrescrito T indica a matriz transposta.

Calcule o determinante dessa relação para descobrir que uma matriz de rotação tem determinante ± 1. Em particular,

${\ displaystyle {\ begin {alinhados} 1 = \ det (\ mathbf {I}) & = \ det \ left (\ mathbf {R} ^ {\ mathsf {T}} \ mathbf {R} \ right) = \ det \ left (\ mathbf {R} ^ {\ mathsf {T}} \ right) \ det (\ mathbf {R}) = \ det (\ mathbf {R}) ^ {2} \\\ Longrightarrow \ qquad \ det (\ mathbf {R}) & = \ pm 1. \ end {alinhado}}}$

Uma matriz de rotação com determinante +1 é uma rotação adequada, e outra com determinante negativo -1 é uma rotação imprópria , ou seja, uma reflexão combinada com uma rotação adequada.

Agora será mostrado que uma matriz de rotação adequada R tem pelo menos um vetor invariante n , ou seja, Rn = n . Como isso requer que ( R - I ) n = 0 , vemos que o vetor n deve ser um autovetor da matriz R com autovalor λ = 1 . Portanto, isso é equivalente a mostrar que det ( R - I ) = 0 .

Use as duas relações

${\ displaystyle \ det (- \ mathbf {A}) = (- 1) ^ {3} \ det (\ mathbf {A}) = - \ det (\ mathbf {A}) \ quad}$

para qualquer matriz A 3 × 3 e

${\ displaystyle \ det \ left (\ mathbf {R} ^ {- 1} \ right) = 1 \ quad}$

(uma vez que det ( R ) = 1 ) para calcular

${\ displaystyle {\ begin {alinhados} & \ det (\ mathbf {R} - \ mathbf {I}) = \ det \ left ((\ mathbf {R} - \ mathbf {I}) ^ {\ mathsf {T }} \ direita) \\ {} = {} & \ det \ left (\ mathbf {R} ^ {\ mathsf {T}} - \ mathbf {I} \ right) = \ det \ left (\ mathbf {R } ^ {- 1} - \ mathbf {R} ^ {- 1} \ mathbf {R} \ direita) \\ {} = {} & \ det \ left (\ mathbf {R} ^ {- 1} (\ mathbf {I} - \ mathbf {R}) \ right) = \ det \ left (\ mathbf {R} ^ {- 1} \ right) \, \ det (- (\ mathbf {R} - \ mathbf {I })) \\ {} = {} & - \ det (\ mathbf {R} - \ mathbf {I}) \\ [3pt] \ Longrightarrow \ 0 = {} & \ det (\ mathbf {R} - \ mathbf {I}). \ end {alinhado}}}$

Isso mostra que λ = 1 é uma raiz (solução) da equação característica , ou seja,

${\ displaystyle \ det (\ mathbf {R} - \ lambda \ mathbf {I}) = 0 \ quad {\ hbox {para}} \ quad \ lambda = 1.}$

Em outras palavras, a matriz R - I é singular e possui um kernel diferente de zero , ou seja, há pelo menos um vetor diferente de zero, digamos n , para o qual

${\ displaystyle (\ mathbf {R} - \ mathbf {I}) \ mathbf {n} = \ mathbf {0} \ quad \ Longleftrightarrow \ quad \ mathbf {R} \ mathbf {n} = \ mathbf {n}. }$

A linha μ n para μ real é invariante em R , ou seja, μ n é um eixo de rotação. Isso prova o teorema de Euler.

Equivalência de uma matriz ortogonal a uma matriz de rotação

Duas matrizes (representando mapas lineares) são consideradas equivalentes se houver uma mudança de base que torne uma igual à outra. Uma matriz ortogonal adequada é sempre equivalente (neste sentido) à matriz a seguir ou à sua reflexão vertical:

${\ displaystyle \ mathbf {R} \ sim {\ begin {pmatrix} \ cos \ phi & - \ sin \ phi & 0 \\\ sin \ phi & \ cos \ phi & 0 \\ 0 & 0 & 1 \\\ end {pmatrix}} , \ qquad 0 \ leq \ phi \ leq 2 \ pi.}$

Então, qualquer matriz ortogonal é uma rotação ou uma rotação imprópria . Uma matriz ortogonal geral tem apenas um autovalor real, +1 ou -1. Quando é +1, a matriz é uma rotação. Quando −1, a matriz é uma rotação imprópria.

Se R tem mais do que um vector de invariante então φ = 0 e R = I . Qualquer vector é um vector invariante de I .

Excursão na teoria da matriz

Para provar a equação anterior, alguns fatos da teoria das matrizes devem ser relembrados.

Uma matriz A m × m tem m autovetores ortogonais se e somente se A for normal , isto é, se A ^† A = AA ^† . Este resultado é equivalente a afirmar que as matrizes normais podem ser levadas à forma diagonal por uma transformação de similaridade unitária:

${\ displaystyle \ mathbf {A} \ mathbf {U} = \ mathbf {U} \; \ operatorname {diag} (\ alpha _ {1}, \ ldots, \ alpha _ {m}) \ quad \ Longleftrightarrow \ quad \ mathbf {U} ^ {\ dagger} \ mathbf {A} \ mathbf {U} = \ operatorname {diag} (\ alpha _ {1}, \ ldots, \ alpha _ {m}),}$

e U é unitário, ou seja,

${\ displaystyle \ mathbf {U} ^ {\ dagger} = \ mathbf {U} ^ {- 1}.}$

Os autovalores α ₁ , ..., α _m são raízes da equação característica. Se a matriz A for unitária (e observe que as matrizes unitárias são normais), então

${\ displaystyle \ left (\ mathbf {U} ^ {\ dagger} \ mathbf {A} \ mathbf {U} \ right) ^ {\ dagger} = \ operatorname {diag} \ left (\ alpha _ {1} ^ {*}, \ ldots, \ alpha _ {m} ^ {*} \ right) = \ mathbf {U} ^ {\ dagger} \ mathbf {A} ^ {- 1} \ mathbf {U} = \ operatorname { diag} \ left ({\ frac {1} {\ alpha _ {1}}}, \ ldots, {\ frac {1} {\ alpha _ {m}}} \ right)}$

e segue-se que os valores próprios de uma matriz unitária estão no círculo unitário no plano complexo:

${\ displaystyle \ alpha _ {k} ^ {*} = {\ frac {1} {\ alpha _ {k}}} \ quad \ Longleftrightarrow \ quad \ alpha _ {k} ^ {*} \ alpha _ {k } = \ left | \ alpha _ {k} \ right | ^ {2} = 1, \ qquad k = 1, \ ldots, m.}$

Além disso, uma matriz ortogonal (real unitária) tem autovalores no círculo unitário do plano complexo. Além disso, como sua equação característica (um polinômio de ordem m em λ ) tem coeficientes reais, segue-se que suas raízes aparecem em pares conjugados complexos, isto é, se α é uma raiz, então α ^∗ também é . Existem 3 raízes, portanto, pelo menos uma delas deve ser puramente real (+1 ou -1).

Depois lembrança desses fatos gerais da teoria da matriz, voltamos para a matriz de rotação R . Conclui-se de sua realidade e ortogonalidade que podemos encontrar um U tal que:

${\ displaystyle \ mathbf {R} \ mathbf {U} = \ mathbf {U} {\ begin {pmatrix} e ^ {i \ phi} & 0 & 0 \\ 0 & e ^ {- i \ phi} & 0 \\ 0 & 0 & \ pm 1 \\\ end {pmatrix}}}$

Se uma matriz U puder ser encontrada que forneça a forma acima, e houver apenas um componente puramente real e é -1, então definimos R como uma rotação imprópria. Consideremos apenas o caso, então, de matrizes R que são rotações próprias (o terceiro autovalor é apenas 1). A terceira coluna da matriz 3 × 3 U será então igual ao vetor invariante n . Escrevendo u ₁ e u ₂ para as duas primeiras colunas de U , esta equação dá

${\ displaystyle \ mathbf {R} \ mathbf {u} _ {1} = e ^ {i \ phi} \, \ mathbf {u} _ {1} \ quad {\ hbox {and}} \ quad \ mathbf { R} \ mathbf {u} _ {2} = e ^ {- i \ phi} \, \ mathbf {u} _ {2}.}$

Se u ₁ tem valores próprios 1, então φ = 0 e L ₂ tem também um valor próprio, o que implica que, nesse caso, R = E .

Finalmente, a equação da matriz é transformada por meio de uma matriz unitária,

${\ displaystyle \ mathbf {R} \ mathbf {U} {\ begin {pmatrix} {\ frac {1} {\ sqrt {2}}} & {\ frac {i} {\ sqrt {2}}} & 0 \ \ {\ frac {1} {\ sqrt {2}}} & {\ frac {-i} {\ sqrt {2}}} & 0 \\ 0 & 0 & 1 \\\ end {pmatrix}} = \ mathbf {U} \ underbrace {{\ begin {pmatrix} {\ frac {1} {\ sqrt {2}}} & {\ frac {i} {\ sqrt {2}}} & 0 \\ {\ frac {1} {\ sqrt { 2}}} & {\ frac {-i} {\ sqrt {2}}} & 0 \\ 0 & 0 & 1 \\\ end {pmatrix}} {\ begin {pmatrix} {\ frac {1} {\ sqrt {2} }} & {\ frac {1} {\ sqrt {2}}} & 0 \\ {\ frac {-i} {\ sqrt {2}}} & {\ frac {i} {\ sqrt {2}}} & 0 \\ 0 & 0 & 1 \\\ end {pmatrix}}} _ {= \; \ mathbf {I}} {\ begin {pmatrix} e ^ {i \ phi} & 0 & 0 \\ 0 & e ^ {- i \ phi} & 0 \ \ 0 & 0 & 1 \\\ end {pmatrix}} {\ begin {pmatrix} {\ frac {1} {\ sqrt {2}}} & {\ frac {i} {\ sqrt {2}}} & 0 \\ {\ frac {1} {\ sqrt {2}}} & {\ frac {-i} {\ sqrt {2}}} & 0 \\ 0 & 0 & 1 \\\ end {pmatrix}}}$

que dá

${\ displaystyle \ mathbf {U '} ^ {\ dagger} \ mathbf {R} \ mathbf {U'} = {\ begin {pmatrix} \ cos \ phi & - \ sin \ phi & 0 \\\ sin \ phi & \ cos \ phi & 0 \\ 0 & 0 & 1 \\\ end {pmatriz}} \ quad {\ text {com}} \ quad \ mathbf {U '} = \ mathbf {U} {\ begin {pmatriz} {\ frac {1 } {\ sqrt {2}}} & {\ frac {i} {\ sqrt {2}}} & 0 \\ {\ frac {1} {\ sqrt {2}}} & {\ frac {-i} { \ sqrt {2}}} & 0 \\ 0 & 0 & 1 \\\ end {pmatrix}}.}$

As colunas de U ′ são ortonormais. A terceira coluna ainda é n , as outras duas colunas são perpendiculares a n . Agora podemos ver como nossa definição de rotação inadequada corresponde à interpretação geométrica: uma rotação inadequada é uma rotação em torno de um eixo (aqui, o eixo correspondente à terceira coordenada) e uma reflexão em um plano perpendicular a esse eixo. Se nos restringirmos apenas a matrizes com determinante 1, podemos então ver que elas devem ser rotações adequadas. Este resultado implica que qualquer matriz ortogonal R correspondente a uma rotação adequada é equivalente a uma rotação sobre um ângulo φ em torno de um eixo n .

Classes de equivalência

O traço (soma dos elementos diagonais) da matriz de rotação real dada acima é 1 + 2 cos φ . Uma vez que um traço é invariante sob uma transformação de similaridade de matriz ortogonal,

${\ displaystyle \ mathrm {Tr} \ left [\ mathbf {A} \ mathbf {R} \ mathbf {A} ^ {\ mathsf {T}} \ right] = \ mathrm {Tr} \ left [\ mathbf {R } \ mathbf {A} ^ {\ mathsf {T}} \ mathbf {A} \ right] = \ mathrm {Tr} [\ mathbf {R}] \ quad {\ text {com}} \ quad \ mathbf {A } ^ {\ mathsf {T}} = \ mathbf {A} ^ {- 1},}$

segue-se que todas as matrizes que são equivalentes a R por tais transformações de matriz ortogonal têm o mesmo traço: o traço é uma função de classe . Essa transformação de matriz é claramente uma relação de equivalência , ou seja, todas as matrizes equivalentes formam uma classe de equivalência.

Na verdade, todas as matrizes de rotação 3 × 3 de rotação apropriada formam um grupo , geralmente denotado por SO (3) (o grupo ortogonal especial em 3 dimensões) e todas as matrizes com o mesmo traço formam uma classe de equivalência neste grupo. Todos os elementos de tal classe de equivalência compartilham seu ângulo de rotação , mas todas as rotações são em torno de eixos diferentes. Se n é um autovetor de R com autovalor 1, então An também é um autovetor de ARA ^T , também com autovalor 1. A menos que A = I , n e An sejam diferentes.

Formulários

Geradores de rotações

Suponha que especificamos um eixo de rotação por um vetor unitário [ x , y , z ] , e suponha que temos uma rotação infinitamente pequena do ângulo Δ θ em torno desse vetor. Expandindo a matriz de rotação como uma adição infinita e tomando a abordagem de primeira ordem, a matriz de rotação Δ R é representada como:

${\ displaystyle \ Delta R = {\ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}} + {\ begin {bmatrix} 0 & z & -y \\ - z & 0 & x \\ y & -x & 0 \ end {bmatrix} } \, \ Delta \ theta = \ mathbf {I} + \ mathbf {A} \, \ Delta \ theta.}$

Uma rotação finita através do ângulo θ em torno deste eixo pode ser vista como uma sucessão de pequenas rotações em torno do mesmo eixo. Aproximando Δ θ como θ/Nonde N é um grande número, uma rotação de θ em torno do eixo pode ser representada como:

${\ displaystyle R = \ left (\ mathbf {1} + {\ frac {\ mathbf {A} \ theta} {N}} \ right) ^ {N} \ approx e ^ {\ mathbf {A} \ theta} .}$

Pode-se ver que o teorema de Euler afirma essencialmente que todas as rotações podem ser representadas nesta forma. O produto Um θ é o "gerador" de rotação particular, sendo o vector ( x , y , z ) associada com a matriz A . Isso mostra que a matriz de rotação e o formato do ângulo do eixo estão relacionados pela função exponencial.

Pode-se derivar uma expressão simples para o gerador G . Começa-se com um plano arbitrário (no espaço euclidiano) definido por um par de vetores unitários perpendiculares a e b . Neste plano, pode-se escolher um vetor arbitrário x com y perpendicular . Uma então resolve de y em termos de x e substituindo em uma expressão para uma rotação num plano origina a matriz de rotação R que inclui o gerador G = bA ^T - ab ^T .

${\ displaystyle {\ begin {alinhados} \ mathbf {x} & = \ mathbf {a} \ cos \ alpha + \ mathbf {b} \ sin \ alpha \\\ mathbf {y} & = - \ mathbf {a} \ sin \ alpha + \ mathbf {b} \ cos \ alpha \\ [8pt] \ cos \ alpha & = \ mathbf {a} ^ {\ mathsf {T}} \ mathbf {x} \\\ sin \ alpha & = \ mathbf {b} ^ {\ mathsf {T}} \ mathbf {x} \\ [8px] \ mathbf {y} & = - \ mathbf {ab} ^ {\ mathsf {T}} \ mathbf {x} + \ mathbf {ba} ^ {\ mathsf {T}} \ mathbf {x} = \ left (\ mathbf {ba} ^ {\ mathsf {T}} - \ mathbf {ab} ^ {\ mathsf {T}} \ direita) \ mathbf {x} \\ [8px] \ mathbf {x} '& = \ mathbf {x} \ cos \ beta + \ mathbf {y} \ sin \ beta \\ & = \ left (\ mathbf { I} \ cos \ beta + \ left (\ mathbf {ba} ^ {\ mathsf {T}} - \ mathbf {ab} ^ {\ mathsf {T}} \ right) \ sin \ beta \ right) \ mathbf { x} \\ [8px] \ mathbf {R} & = \ mathbf {I} \ cos \ beta + \ left (\ mathbf {ba} ^ {\ mathsf {T}} - \ mathbf {ab} ^ {\ mathsf {T}} \ right) \ sin \ beta \\ & = \ mathbf {I} \ cos \ beta + \ mathbf {G} \ sin \ beta \\ [8px] \ mathbf {G} & = \ mathbf {ba } ^ {\ mathsf {T}} - \ mathbf {ab} ^ {\ mathsf {T}} \ end {alinhado}}}$

Para incluir vetores fora do plano na rotação, é necessário modificar a expressão acima para R incluindo dois operadores de projeção que particionam o espaço. Esta matriz de rotação modificada pode ser reescrita como uma função exponencial .

${\ displaystyle {\ begin {alinhados} \ mathbf {P_ {ab}} & = - \ mathbf {G} ^ {2} \\\ mathbf {R} & = \ mathbf {I} - \ mathbf {P_ {ab }} + \ left (\ mathbf {I} \ cos \ beta + \ mathbf {G} \ sin \ beta \ right) \ mathbf {P_ {ab}} = e ^ {\ mathbf {G} \ beta} \ end {alinhado}}}$

A análise é geralmente mais fácil em termos desses geradores, em vez da matriz de rotação completa. A análise em termos dos geradores é conhecida como álgebra de Lie do grupo de rotação.

Quatérnions

Segue do teorema de Euler que a orientação relativa de qualquer par de sistemas de coordenadas pode ser especificada por um conjunto de três números independentes. Às vezes, um quarto número redundante é adicionado para simplificar as operações com álgebra de quatérnio. Três desses números são os cossenos de direção que orientam o vetor próprio. O quarto é o ângulo sobre o autovetor que separa os dois conjuntos de coordenadas. Esse conjunto de quatro números é chamado de quaternion .

Embora o quatérnio, conforme descrito acima, não envolva números complexos , se os quatérnios são usados ​​para descrever duas rotações sucessivas, eles devem ser combinados usando a álgebra de quatérnios não comutativa derivada por William Rowan Hamilton através do uso de números imaginários.

O cálculo de rotação por meio de quatérnions veio substituir o uso de cossenos de direção em aplicações aeroespaciais por meio da redução dos cálculos necessários e da capacidade de minimizar erros de arredondamento . Além disso, em computação gráfica, a capacidade de realizar interpolação esférica entre quatérnios com relativa facilidade é valiosa.

Generalizações

Em dimensões superiores, qualquer movimento rígido que preserva um ponto na dimensão 2 n ou 2 n + 1 é uma composição de no máximo n rotações em planos ortogonais de rotação , embora esses planos não precisem ser determinados exclusivamente, e um movimento rígido pode fixar múltiplos machados.

Um movimento rígido em três dimensões que não necessariamente fixa um ponto é um "movimento de parafuso". Isso ocorre porque uma composição de uma rotação com uma translação perpendicular ao eixo é uma rotação em torno de um eixo paralelo, enquanto a composição com uma translação paralela ao eixo produz um movimento de parafuso; veja o eixo do parafuso . Isso dá origem à teoria do parafuso .

Veja também

• Ângulos de Euler
• Parâmetros de Euler-Rodrigues
• Formalismos de rotação em três dimensões
• Operador de rotação (espaço vetorial)
• Velocidade angular
• Rotação em torno de um eixo fixo
• Matriz exponencial
• Representação eixo-ângulo
• Grupo de rotação 3D
• Teorema de Chasles (cinemática) , para uma extensão sobre deslocamentos gerais de corpos rígidos.

Notas

Referências

Este artigo incorpora material do artigo do Citizendium " Teorema de Euler (rotação) ", que é licenciado pela Creative Commons Attribution-ShareAlike 3.0 Unported License, mas não pela GFDL .

• O teorema de Euler e sua prova estão contidos nos parágrafos 24-26 do apêndice ( Additamentum . Pp. 201-203) de L. Eulero (Leonhard Euler) , Formulas generales pro translatione quacunque corporum rigidorum (Fórmulas gerais para a tradução de corpos rígidos arbitrários ), apresentado à Academia de São Petersburgo em 9 de outubro de 1775 e publicado pela primeira vez em Novi Commentarii academiae scientiarum Petropolitanae 20 , 1776, pp. 189–207 (E478) e foi reimpresso em Theoria motus corporum rigidorum , ed. nova, 1790, pp. 449-460 (E478a) e mais tarde em suas obras completas Opera Omnia , Série 2, Volume 9 , pp. 84-98.
• Palais, Bob; Palais, Richard; Rodi, Stephen (2009). "Um olhar desorientador para o teorema de Euler no eixo de uma rotação". American Mathematical Monthly . 116 (10): 892–909. doi : 10.4169 / 000298909x477014 .

links externos

• Tratado original de Euler no Arquivo de Euler : entrada em E478 , primeira publicação 1776 ( pdf )
• Texto original de Euler (em latim) e tradução em inglês (por Johan Sten)
• Projeto de demonstração de Wolfram para o teorema da rotação de Euler (por Tom Verhoeff)