Segunda forma fundamental - Second fundamental form

Na geometria diferencial , a segunda forma fundamental (ou tensor de forma ) é uma forma quadrática no plano tangente de uma superfície lisa no espaço euclidiano tridimensional , geralmente denotada por (leia-se "dois"). Junto com a primeira forma fundamental , serve para definir invariantes extrínsecos da superfície, suas curvaturas principais . Mais geralmente, tal forma quadrática é definida para uma subvariedade imersa suave em uma variedade Riemanniana . ${\ displaystyle \ mathrm {I \! I}}$

Superfície em R ³

Motivação

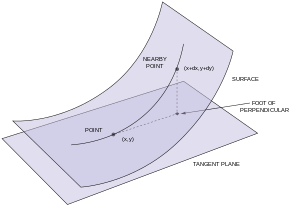
A segunda forma fundamental de uma superfície paramétrica S em R ³ foi introduzida e estudada por Gauss . Em primeiro lugar, suponha que a superfície seja o gráfico de uma função duas vezes continuamente diferenciável , z = f ( x , y ) , e que o plano z = 0 seja tangente à superfície na origem. Em seguida, f e as suas derivadas parciais relativamente a x e y desaparecer em (0,0). Portanto, a expansão de Taylor de f em (0,0) começa com termos quadráticos:

${\ displaystyle z = L {\ frac {x ^ {2}} {2}} + Mxy + N {\ frac {y ^ {2}} {2}} + {\ text {termos de ordem superior}} \, ,}$

e a segunda forma fundamental na origem nas coordenadas ( x , y ) é a forma quadrática

${\ displaystyle L \, dx ^ {2} + 2M \, dx \, dy + N \, dy ^ {2} \ ,.}$

Para um ponto suave P em S , pode-se escolher o sistema de coordenadas de modo que o plano z de coordenadas seja tangente a S em P e definir a segunda forma fundamental da mesma maneira.

Notação clássica

A segunda forma fundamental de uma superfície paramétrica geral é definida como segue. Seja r = r ( u , v ) uma parametrização regular de uma superfície em R ³ , onde r é uma função de valor vetorial suave de duas variáveis. É comum denotar as derivadas parciais de r em relação a u e v por r _u e r _v . A regularidade da parametrização significa que r _u e r _v são linearmente independentes para qualquer ( u , v ) no domínio de r e, portanto, abrangem o plano tangente a S em cada ponto. Equivalentemente, o produto vetorial r _u × r _v é um vetor diferente de zero normal à superfície. A parametrização, portanto, define um campo de vetores normais unitários n :

${\ displaystyle \ mathbf {n} = {\ frac {\ mathbf {r} _ {u} \ times \ mathbf {r} _ {v}} {| \ mathbf {r} _ {u} \ times \ mathbf { r} _ {v} |}} \ ,.}$

A segunda forma fundamental é geralmente escrita como

${\ displaystyle \ mathrm {I \! I} = L \, du ^ {2} + 2M \, du \, dv + N \, dv ^ {2} \ ,,}$

sua matriz na base { r _u , r _v } do plano tangente é

${\ displaystyle {\ begin {bmatrix} L&M \\ M&N \ end {bmatrix}} \ ,.}$

Os coeficientes L , M , N em um determinado ponto no plano uv paramétrico são dados pelas projeções das derivadas parciais de r naquele ponto na linha normal para S e podem ser calculados com a ajuda do produto escalar como segue:

${\ displaystyle L = \ mathbf {r} _ {uu} \ cdot \ mathbf {n} \ ,, \ quad M = \ mathbf {r} _ {uv} \ cdot \ mathbf {n} \ ,, \ quad N = \ mathbf {r} _ {vv} \ cdot \ mathbf {n} \ ,.}$

Para um campo de distância com sinal de Hessian H , os coeficientes da segunda forma fundamental podem ser calculados da seguinte forma:

${\ displaystyle L = - \ mathbf {r} _ {u} \ cdot \ mathbf {H} \ cdot \ mathbf {r} _ {u} \ ,, \ quad M = - \ mathbf {r} _ {u} \ cdot \ mathbf {H} \ cdot \ mathbf {r} _ {v} \ ,, \ quad N = - \ mathbf {r} _ {v} \ cdot \ mathbf {H} \ cdot \ mathbf {r} _ {v} \ ,.}$

Notação física

A segunda forma fundamental de uma superfície paramétrica geral S é definida como segue.

Seja r = r ( u ¹ , u ² ) uma parametrização regular de uma superfície em R ³ , onde r é uma função de valor vetorial suave de duas variáveis. É comum denotar as derivadas parciais de r em relação a u ^α por r _α , α = 1, 2 . A regularidade da parametrização significa que r ₁ e r ₂ são linearmente independentes para qualquer ( u ¹ , u ² ) no domínio de r e, portanto, abrangem o plano tangente a S em cada ponto. Equivalentemente, o produto vetorial r ₁ × r ₂ é um vetor diferente de zero normal à superfície. A parametrização, portanto, define um campo de vetores normais unitários n :

${\ displaystyle \ mathbf {n} = {\ frac {\ mathbf {r} _ {1} \ times \ mathbf {r} _ {2}} {| \ mathbf {r} _ {1} \ times \ mathbf { r} _ {2} |}} \ ,.}$

A segunda forma fundamental é geralmente escrita como

${\ displaystyle \ mathrm {I \! I} = b _ {\ alpha \ beta} \, du ^ {\ alpha} \, du ^ {\ beta} \ ,.}$

A equação acima usa a convenção de soma de Einstein .

Os coeficientes b _αβ em um determinado ponto no plano paramétrico u ¹ u ² são dados pelas projeções das segundas derivadas parciais de r naquele ponto na linha normal para S e podem ser calculados em termos do vetor normal n como segue:

${\ displaystyle b _ {\ alpha \ beta} = r _ {\, \ alpha \ beta} ^ {\ \ \, \ gamma} n _ {\ gamma} \,}$

Hipersuperfície em uma variedade Riemanniana

No espaço euclidiano , a segunda forma fundamental é dada por

${\ displaystyle \ mathrm {I \! I} (v, w) = - \ langle d \ nu (v), w \ rangle \ nu}$

onde ν é o mapa de Gauss , e dν a diferencial de ν considerada como uma forma diferencial com valor vetorial , e os colchetes denotam o tensor métrico do espaço euclidiano.

De forma mais geral, em uma variedade Riemanniana, a segunda forma fundamental é uma maneira equivalente de descrever o operador de forma (denotado por S ) de uma hipersuperfície,

${\ displaystyle \ mathrm {I} \! \ mathrm {I} (v, w) = \ langle S (v), w \ rangle n = - \ langle \ nabla _ {v} n, w \ rangle n = \ langle n, \ nabla _ {v} w \ rangle n \ ,,}$

onde ∇ _v w designa o derivado covariante do colector ambiente e n um campo de vectores normais na hipersuperfıcie. (Se a conexão afim não tiver torção , a segunda forma fundamental será simétrica.)

O sinal da segunda forma fundamental depende da escolha da direção de n (que é chamada de co-orientação da hipersuperfície - para superfícies no espaço euclidiano, isso é dado de forma equivalente pela escolha da orientação da superfície).

Generalização para codimensão arbitrária

A segunda forma fundamental pode ser generalizada para codimensão arbitrária . Nesse caso, é uma forma quadrática no espaço tangente com valores no feixe normal e pode ser definida por

${\ displaystyle \ mathrm {I \! I} (v, w) = (\ nabla _ {v} w) ^ {\ bot} \ ,,}$

onde denota a projeção ortogonal da derivada covariante no feixe normal. ${\ displaystyle (\ nabla _ {v} w) ^ {\ bot}}$ ${\ displaystyle \ nabla _ {v} w}$

No espaço euclidiano , o tensor de curvatura de uma subvariedade pode ser descrito pela seguinte fórmula:

${\ displaystyle \ langle R (u, v) w, z \ rangle = \ langle \ mathrm {I} \! \ mathrm {I} (u, z), \ mathrm {I} \! \ mathrm {I} ( v, w) \ rangle - \ langle \ mathrm {I} \! \ mathrm {I} (u, w), \ mathrm {I} \! \ mathrm {I} (v, z) \ rangle.}$

Isso é chamado de equação de Gauss , pois pode ser vista como uma generalização do Teorema Egregium de Gauss .

Para variedades Riemannianas gerais, deve-se adicionar a curvatura do espaço ambiente; se N é uma variedade embutida em uma variedade Riemanniana ( M , g ), então o tensor de curvatura R _N de N com métrica induzida pode ser expresso usando a segunda forma fundamental e R _M , o tensor de curvatura de M :

${\ displaystyle \ langle R_ {N} (u, v) w, z \ rangle = \ langle R_ {M} (u, v) w, z \ rangle + \ langle \ mathrm {I} \! \ mathrm {I } (u, z), \ mathrm {I} \! \ mathrm {I} (v, w) \ rangle - \ langle \ mathrm {I} \! \ mathrm {I} (u, w), \ mathrm { I} \! \ Mathrm {I} (v, z) \ rangle \ ,.}$

Veja também

• Primeira forma fundamental
• Curvatura gaussiana
• Equações de Gauss-Codazzi
• Operador de forma
• Terceira forma fundamental
• Forma única tautológica

Referências

• Guggenheimer, Heinrich (1977). "Capítulo 10. Superfícies". Geometria Diferencial . Dover. ISBN 0-486-63433-7.
• Kobayashi, Shoshichi & Nomizu, Katsumi (1996). Foundations of Differential Geometry, vol. 2 (nova ed.). Wiley-Interscience. ISBN 0-471-15732-5.
• Spivak, Michael (1999). Uma introdução abrangente à geometria diferencial (Volume 3) . Publique ou pereça. ISBN 0-914098-72-1.

links externos

• Steven Verpoort (2008) Geometria da Segunda Forma Fundamental: Propriedades da Curvatura e Aspectos Variacionais da Katholieke Universiteit Leuven .