Multiplicador de Lagrange - Lagrange multiplier

Na otimização matemática , o método dos multiplicadores de Lagrange é uma estratégia para encontrar os máximos e mínimos locais de uma função sujeita a restrições de igualdade (ou seja, sujeita à condição de que uma ou mais equações devem ser satisfeitas exatamente pelos valores escolhidos das variáveis ) Recebeu o nome do matemático Joseph-Louis Lagrange . A idéia básica é converter um problema restrito em uma forma tal que o teste derivativo de um problema irrestrito ainda possa ser aplicado. A relação entre o gradiente da função e os gradientes das restrições leva naturalmente a uma reformulação do problema original, conhecida como função Lagrangiana .

O método pode ser resumido da seguinte forma: para encontrar o máximo ou mínimo de uma função sujeita à restrição de igualdade , forme a função Lagrangiana ${\ displaystyle f (x)}$${\ displaystyle g (x) = 0}$

${\ displaystyle {\ mathcal {L}} (x, \ lambda) = f (x) - \ lambda g (x)}$

e encontre os pontos estacionários de considerados em função de e do multiplicador de Lagrange . A solução correspondente à otimização restrita original é sempre um ponto de sela da função Lagrangiana, que pode ser identificado entre os pontos estacionários a partir da definição da matriz Hessiana com borda . ${\ displaystyle {\ mathcal {L}}}$${\ displaystyle x}$${\ displaystyle \ lambda}$

A grande vantagem deste método é permitir que a otimização seja resolvida sem parametrização explícita em termos de restrições. Como resultado, o método dos multiplicadores de Lagrange é amplamente utilizado para resolver problemas desafiadores de otimização restrita. Além disso, o método dos multiplicadores de Lagrange é generalizado pelas condições de Karush-Kuhn-Tucker , que também podem levar em consideração as restrições de desigualdade da forma . ${\ displaystyle h (\ mathbf {x}) \ leq c}$

Demonstração

O seguinte é conhecido como teorema do multiplicador de Lagrange.

Seja a função objetivo, seja a função de restrição, ambas pertencentes a (isto é, tendo primeiras derivadas contínuas). Deixe ser uma solução ideal para o seguinte problema de otimização, de forma que classifique : ${\ displaystyle f \ colon \ mathbb {R} ^ {n} \ rightarrow \ mathbb {R}}$${\ displaystyle g \ colon \ mathbb {R} ^ {n} \ rightarrow \ mathbb {R} ^ {c}}$${\ displaystyle C ^ {1}}$${\ displaystyle x ^ {*}}$${\ displaystyle Dg (x ^ {*}) = c <n}$

${\ displaystyle {\ text {maximizar}} \ f (x)}$

${\ displaystyle {\ text {sujeito a:}} \ g (x) = 0}$

(Aqui denota a matriz de derivadas parciais .) ${\ displaystyle Dg (x ^ {*})}$${\ displaystyle \ left [{\ frac {\ partial g_ {j}} {\ partial x_ {k}}} \ right]}$

Então existem Lagrange multiplicadores únicas tais que . ${\ displaystyle \ lambda ^ {*} \ in \ mathbb {R} ^ {c}}$${\ displaystyle Df (x ^ {*}) = \ lambda ^ {* T} Dg (x ^ {*})}$

O teorema do multiplicador de Lagrange afirma que em qualquer máximo local (ou mínimo) da função avaliada sob as restrições de igualdade, se a qualificação de restrição se aplica (explicada abaixo), então o gradiente da função (naquele ponto) pode ser expresso como uma combinação linear dos gradientes das restrições (naquele ponto), com os multiplicadores de Lagrange atuando como coeficientes . Isso é equivalente a dizer que qualquer direção perpendicular a todos os gradientes das restrições também é perpendicular ao gradiente da função. Ou ainda, dizendo que a derivada direcional da função é 0 em todas as direções possíveis.

Restrição única

Figura 1: A curva vermelha mostra a restrição g ( x , y ) = c . As curvas azuis são contornos de f ( x , y ) . O ponto onde a restrição vermelha tangencialmente toca um contorno azul é o máximo de f ( x , y ) ao longo da restrição, uma vez que d ₁ > d ₂ .

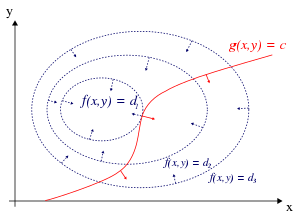
Para o caso de apenas uma restrição e apenas duas variáveis ​​de escolha (conforme exemplificado na Figura 1), considere o problema de otimização

${\ displaystyle {\ text {maximizar}} \ f (x, y)}$

${\ displaystyle {\ text {sujeito a:}} \ g (x, y) = 0}$

(Às vezes, uma constante aditiva é mostrada separadamente em vez de ser incluída , caso em que a restrição é escrita , como na Figura 1.) Assumimos que ambos e têm primeiras derivadas parciais contínuas . Nós introduzimos uma nova variável ( ) chamado de multiplicador de Lagrange (ou Lagrange indeterminado multiplicador ) e estudar a função de Lagrange (ou de Lagrange ou expressão de Lagrange ) definido pela ${\ displaystyle g}$${\ displaystyle g (x, y) = c}$${\ displaystyle f}$${\ displaystyle g}$${\ displaystyle \ lambda}$

${\ displaystyle {\ mathcal {L}} (x, y, \ lambda) = f (x, y) - \ lambda g (x, y),}$

onde o termo pode ser adicionado ou subtraído. Se é um máximo de para o problema restrito original e , então existe tal que ( ) é um ponto estacionário para a função de Lagrange (pontos estacionários são aqueles pontos onde as primeiras derivadas parciais de são zero). A suposição é chamada de qualificação de restrição. No entanto, nem todos os pontos estacionários fornecem uma solução para o problema original, pois o método dos multiplicadores de Lagrange fornece apenas uma condição necessária para a otimização em problemas restritos. Também existem condições suficientes para um mínimo ou máximo , mas se uma solução candidata particular satisfizer as condições suficientes, só é garantido que essa solução seja a melhor localmente - ou seja, é melhor do que quaisquer pontos próximos permitidos. O ótimo global pode ser encontrado comparando os valores da função objetivo original nos pontos que satisfazem as condições necessárias e localmente suficientes. ${\ displaystyle \ lambda}$${\ displaystyle f (x_ {0}, y_ {0})}$${\ displaystyle f (x, y)}$${\ displaystyle \ nabla g (x_ {0}, y_ {0}) \ neq 0}$${\ displaystyle \ lambda _ {0}}$${\ displaystyle x_ {0}, y_ {0}, \ lambda _ {0}}$${\ displaystyle {\ mathcal {L}}}$${\ displaystyle \ nabla g \ neq 0}$

O método dos multiplicadores de Lagrange se baseia na intuição de que, no máximo, f ( x , y ) não pode estar aumentando na direção de qualquer ponto vizinho que também tenha g = 0 . Se fosse, poderíamos caminhar ao longo de g = 0 para subir, o que significa que o ponto de partida não era realmente o máximo. Visto dessa maneira, é um análogo exato de testar se a derivada de uma função irrestrita é 0, ou seja, estamos verificando se a derivada direcional é 0 em qualquer direção relevante (viável).

Podemos visualizar os contornos de f dados por f ( x , y ) = d para vários valores de d , e o contorno de g dado por g ( x , y ) = c .

Suponha que andemos ao longo da linha de contorno com g = c . Estamos interessados ​​em encontrar pontos onde f quase não muda à medida que caminhamos, uma vez que esses pontos podem ser máximos.

Isso pode acontecer de duas maneiras:

1. Poderíamos tocar uma linha de contorno de f , uma vez que, por definição, f não muda à medida que caminhamos ao longo de suas linhas de contorno. Isto significaria que as tangentes às linhas de contorno de f e g são paralelos aqui.
2. Alcançamos um "nível" parte de f , o que significa que f não muda em nenhuma direção.

Para verificar a primeira possibilidade (que tocar uma linha de contorno de f ), aviso de que uma vez que a inclinação de uma função é perpendicular às linhas de contorno, as tangentes às linhas de contorno de f e g são paralelos se e somente se os gradientes de f e g são paralelos. Assim, queremos pontos ( x , y ) onde g ( x , y ) = c e

${\ displaystyle \ nabla _ {x, y} f = \ lambda \, \ nabla _ {x, y} g,}$

para alguns ${\ displaystyle \ lambda}$

Onde

${\ displaystyle \ nabla _ {x, y} f = \ left ({\ frac {\ partial f} {\ partial x}}, {\ frac {\ partial f} {\ partial y}} \ right), \ qquad \ nabla _ {x, y} g = \ left ({\ frac {\ partial g} {\ partial x}}, {\ frac {\ partial g} {\ partial y}} \ right)}$

são os respectivos gradientes. A constante é necessária porque, embora os dois vetores de gradiente sejam paralelos, as magnitudes dos vetores de gradiente geralmente não são iguais. Essa constante é chamada de multiplicador de Lagrange. (Em algumas convenções é precedido por um sinal de menos). ${\ displaystyle \ lambda}$${\ displaystyle \ lambda}$

Observe que este método também resolve a segunda possibilidade, que f é nível: se f é nível, então seu gradiente é zero, e a configuração é uma solução independentemente de . ${\ displaystyle \ lambda = 0}$${\ displaystyle \ nabla _ {x, y} g}$

Para incorporar essas condições em uma equação, introduzimos uma função auxiliar

${\ displaystyle {\ mathcal {L}} (x, y, \ lambda) = f (x, y) - \ lambda g (x, y),}$

e resolver

${\ displaystyle \ nabla _ {x, y, \ lambda} {\ mathcal {L}} (x, y, \ lambda) = 0.}$

Observe que isso equivale a resolver três equações em três incógnitas. Este é o método dos multiplicadores de Lagrange.

Observe que implica , como a derivada parcial de em relação a é , que claramente é zero se e somente se . ${\ displaystyle \ nabla _ {\ lambda} {\ mathcal {L}} (x, y, \ lambda) = 0}$${\ displaystyle g (x, y) = 0}$${\ displaystyle {\ mathcal {L}}}$${\ displaystyle \ lambda}$${\ displaystyle -g (x, y)}$${\ displaystyle g (x, y) = 0}$

Para resumir

${\ displaystyle \ nabla _ {x, y, \ lambda} {\ mathcal {L}} (x, y, \ lambda) = 0 \ iff {\ begin {cases} \ nabla _ {x, y} f (x , y) = \ lambda \, \ nabla _ {x, y} g (x, y) \\ g (x, y) = 0 \ end {casos}}}$

O método generaliza prontamente para funções em variáveis ${\ displaystyle n}$

${\ displaystyle \ nabla _ {x_ {1}, \ dots, x_ {n}, \ lambda} {\ mathcal {L}} (x_ {1}, \ dots, x_ {n}, \ lambda) = 0}$

o que equivale a resolver n + 1 equações em n + 1 incógnitas.

Os extremos restritos de f são pontos críticos da Lagrangiana , mas não são necessariamente extremos locais de (consulte o Exemplo 2 abaixo). ${\ displaystyle {\ mathcal {L}}}$${\ displaystyle {\ mathcal {L}}}$

Pode-se reformular o Lagrangiano como um Hamiltoniano , caso em que as soluções são mínimos locais para o Hamiltoniano. Isso é feito na teoria de controle ótimo , na forma do princípio mínimo de Pontryagin .

O fato de as soluções do Lagrangiano não serem necessariamente extremas também apresenta dificuldades para a otimização numérica. Isso pode ser resolvido calculando a magnitude do gradiente, já que os zeros da magnitude são necessariamente mínimos locais, conforme ilustrado no exemplo de otimização numérica .

Múltiplas restrições

Figura 2: Um parabolóide restringido ao longo de duas linhas que se cruzam.

Figura 3: Mapa de contorno da Figura 2.

O método dos multiplicadores de Lagrange pode ser estendido para resolver problemas com múltiplas restrições usando um argumento semelhante. Considere um parabolóide sujeito a duas restrições de linha que se cruzam em um único ponto. Como a única solução viável, esse ponto é obviamente um extremo restrito. No entanto, o conjunto de níveis de é claramente não paralelo a nenhuma das restrições no ponto de interseção (consulte a Figura 3); em vez disso, é uma combinação linear dos gradientes das duas restrições. No caso de restrições múltiplas, isso será o que buscamos em geral: o método de Lagrange busca pontos não nos quais o gradiente de seja múltiplo de qualquer gradiente de uma única restrição necessariamente, mas em que seja uma combinação linear de todas as restrições ' gradientes. ${\ displaystyle f}$${\ displaystyle f}$

Concretamente, suponha que temos restrições e estamos caminhando ao longo do conjunto de pontos que nos satisfazem . Cada ponto no contorno de uma dada função de restrição tem um espaço de direções permitidas: o espaço de vetores perpendiculares a . O conjunto de direções permitidas por todas as restrições é, portanto, o espaço de direções perpendicular a todos os gradientes das restrições. Denote este espaço de movimentos permitidos por e denote a extensão dos gradientes das restrições por . Então , o espaço de vetores perpendicular a cada elemento de . ${\ displaystyle M}$${\ displaystyle g_ {i} (\ mathbf {x}) = 0, i = 1, \ dots, M}$${\ displaystyle \ mathbf {x}}$${\ displaystyle g_ {i}}$${\ displaystyle \ nabla g_ {i} (\ mathbf {x})}$${\ displaystyle A}$${\ displaystyle S}$${\ displaystyle A = S ^ {\ perp}}$${\ displaystyle S}$

Ainda estamos interessados ​​em encontrar pontos que não mudem à medida que caminhamos, uma vez que esses pontos podem ser extremos (restritos). Portanto, buscamos de forma que qualquer direção permitida de movimento para longe de seja perpendicular a (caso contrário, poderíamos aumentar movendo ao longo dessa direção permitida). Em outras palavras ,. Assim, existem escalares tais que ${\ displaystyle f}$${\ displaystyle \ mathbf {x}}$${\ displaystyle \ mathbf {x}}$${\ displaystyle \ nabla f (\ mathbf {x})}$${\ displaystyle f}$${\ displaystyle \ nabla f (\ mathbf {x}) \ in A ^ {\ perp} = S}$${\ displaystyle \ lambda _ {1}, \ lambda _ {2}, .... \ lambda _ {M}}$

${\ displaystyle \ nabla f (\ mathbf {x}) = \ sum _ {k = 1} ^ {M} \ lambda _ {k} \, \ nabla g_ {k} (\ mathbf {x}) \ quad \ iff \ quad \ nabla f (\ mathbf {x}) - \ sum _ {k = 1} ^ {M} {\ lambda _ {k} \ nabla g_ {k} (\ mathbf {x})} = 0. }$

Esses escalares são os multiplicadores de Lagrange. Agora temos deles, um para cada restrição. ${\ displaystyle M}$

Como antes, apresentamos uma função auxiliar

${\ displaystyle {\ mathcal {L}} \ left (x_ {1}, \ ldots, x_ {n}, \ lambda _ {1}, \ ldots, \ lambda _ {M} \ right) = f \ left ( x_ {1}, \ ldots, x_ {n} \ right) - \ sum \ limits _ {k = 1} ^ {M} {\ lambda _ {k} g_ {k} \ left (x_ {1}, \ ldots, x_ {n} \ right)}}$

e resolver

${\ displaystyle \ nabla _ {x_ {1}, \ ldots, x_ {n}, \ lambda _ {1}, \ ldots, \ lambda _ {M}} {\ mathcal {L}} (x_ {1}, \ ldots, x_ {n}, \ lambda _ {1}, \ ldots, \ lambda _ {M}) = 0 \ iff {\ begin {cases} \ nabla f (\ mathbf {x}) - \ sum _ { k = 1} ^ {M} {\ lambda _ {k} \, \ nabla g_ {k} (\ mathbf {x})} = 0 \\ g_ {1} (\ mathbf {x}) = \ cdots = g_ {M} (\ mathbf {x}) = 0 \ end {casos}}}$

o que equivale a resolver equações em incógnitas. ${\ displaystyle n + M}$${\ displaystyle n + M}$

A suposição de qualificação de restrição quando há várias restrições é que os gradientes de restrição no ponto relevante são linearmente independentes.

Formulação moderna por meio de variedades diferenciáveis

O problema de encontrar máximos e mínimos locais sujeitos a restrições pode ser generalizado para encontrar máximos e mínimos locais em uma variedade diferenciável . A seguir, não é necessário que seja um espaço euclidiano, ou mesmo uma variedade Riemanniana. Todas as aparências do gradiente (que depende da escolha da métrica Riemanniana) podem ser substituídas pela derivada externa . ${\ displaystyle M}$${\ displaystyle M}$${\ displaystyle \ nabla}$ ${\ displaystyle d}$

Restrição única

Deixe ser uma variedade suave de dimensão . Suponha que desejamos encontrar os pontos estacionários de uma função suave quando restrita à subvariedade definida por onde está uma função suave para a qual 0 é um valor regular . ${\ displaystyle M}$${\ displaystyle m}$${\ displaystyle x}$${\ displaystyle f: M \ to \ mathbb {R}}$${\ displaystyle N}$${\ displaystyle g (x) = 0,}$${\ displaystyle g: M \ to \ mathbb {R}}$

Deixe e seja os derivados exteriores . Estacionaridade para a restrição em significa Equivalentemente, o kernel contém Em outras palavras, e são formas 1 proporcionais. Para isso, é necessário e suficiente que o seguinte sistema de equações seja válido: ${\ displaystyle df}$${\ displaystyle dg}$${\ displaystyle f | _ {N}}$${\ displaystyle x \ in N}$${\ displaystyle d (f | _ {N}) _ {x} = 0.}$${\ displaystyle \ ker (df_ {x})}$${\ displaystyle T_ {x} N = \ ker (dg_ {x}).}$${\ displaystyle df_ {x}}$${\ displaystyle dg_ {x}}$${\ displaystyle m (m-1) / 2}$

${\ displaystyle df_ {x} \ wedge dg_ {x} = 0 \ in \ Lambda ^ {2} (T_ {x} ^ {*} M)}$

onde denota o produto exterior . Os pontos estacionários são as soluções do sistema de equações acima mais a restrição. Observe que as equações não são independentes, pois o lado esquerdo da equação pertence à subvariedade de consistir em elementos decomponíveis . ${\ displaystyle \ wedge}$${\ displaystyle x}$${\ displaystyle g (x) = 0.}$${\ displaystyle {\ tfrac {1} {2}} m (m-1)}$${\ displaystyle \ Lambda ^ {2} (T_ {x} ^ {*} M)}$

Nesta formulação, não é necessário encontrar explicitamente o multiplicador de Lagrange, um número tal que${\ displaystyle \ lambda}$${\ displaystyle df_ {x} = \ lambda \, dg_ {x}.}$

Múltiplas restrições

Let and be como na seção acima com relação ao caso de uma única restrição. Em vez da função descrita aqui, considere agora uma função suave com funções de componente para a qual é um valor regular . Let ser a subvariedade de definido por${\ displaystyle M}$${\ displaystyle f}$${\ displaystyle g}$${\ displaystyle G: M \ to \ mathbb {R} ^ {p} (p> 1),}$${\ displaystyle g_ {i}: M \ to \ mathbb {R},}$${\ displaystyle 0 \ in \ mathbb {R} ^ {p}}$${\ displaystyle N}$${\ displaystyle M}$${\ displaystyle G (x) = 0.}$

${\ displaystyle x}$é um ponto estacionário de se e somente se contém . Por conveniência, deixe e onde denota o mapa tangente ou Jacobiano O subespaço tem dimensão menor que a de , a saber e pertence a se e somente se pertence à imagem de Computacionalmente falando, a condição é que pertence ao espaço de linha da matriz de ou equivalentemente, o espaço da coluna da matriz de (a transposta). Se denota o produto exterior das colunas da matriz da condição estacionária para em torna - se ${\ displaystyle f | _ {N}}$${\ displaystyle \ ker (df_ {x})}$${\ displaystyle \ ker (dG_ {x})}$${\ displaystyle L_ {x} = df_ {x}}$${\ displaystyle K_ {x} = dG_ {x},}$${\ displaystyle dG}$${\ displaystyle TM \ to T \ mathbb {R} ^ {p}.}$${\ displaystyle \ ker (K_ {x})}$${\ displaystyle \ ker (L_ {x})}$${\ displaystyle \ dim (\ ker (L_ {x})) = n-1}$${\ displaystyle \ dim (\ ker (K_ {x})) = np.}$ ${\ displaystyle \ ker (K_ {x})}$${\ displaystyle \ ker (L_ {x})}$${\ displaystyle L_ {x} \ in T_ {x} ^ {*} M}$${\ displaystyle K_ {x} ^ {*}: \ mathbb {R} ^ {p *} \ para T_ {x} ^ {*} M.}$${\ displaystyle L_ {x}}$${\ displaystyle K_ {x},}$${\ displaystyle K_ {x} ^ {*}}$${\ displaystyle \ omega _ {x} \ in \ Lambda ^ {p} (T_ {x} ^ {*} M)}$${\ displaystyle K_ {x} ^ {*},}$${\ displaystyle f | _ {N}}$${\ displaystyle x}$

${\ displaystyle L_ {x} \ wedge \ omega _ {x} = 0 \ in \ Lambda ^ {p + 1} \ left (T_ {x} ^ {*} M \ right)}$

Mais uma vez, nesta formulação não é necessário encontrar explicitamente os multiplicadores de Lagrange, os números tais que ${\ displaystyle \ lambda _ {1}, \ ldots, \ lambda _ {p}}$

${\ displaystyle df_ {x} = \ sum _ {i = 1} ^ {p} \ lambda _ {i} d (g_ {i}) _ {x}.}$

Interpretação dos multiplicadores de Lagrange

Freqüentemente, os multiplicadores de Lagrange têm uma interpretação como alguma quantidade de interesse. Por exemplo, ao parametrizar a linha de contorno da restrição, ou seja, se a expressão Lagrangiana é

${\ displaystyle {\ begin {alinhados} & {\ mathcal {L}} (x_ {1}, x_ {2}, \ ldots; \ lambda _ {1}, \ lambda _ {2}, \ ldots; c_ { 1}, c_ {2}, \ ldots) \\ [4pt] = {} & f (x_ {1}, x_ {2}, \ ldots) + \ lambda _ {1} (c_ {1} -g_ {1 } (x_ {1}, x_ {2}, \ ldots)) + \ lambda _ {2} (c_ {2} -g_ {2} (x_ {1}, x_ {2}, \ pontos)) + \ cdots \ end {alinhados}}}$

então

${\ displaystyle {\ frac {\ partial {\ mathcal {L}}} {\ partial c_ {k}}} = \ lambda _ {k}.}$

Portanto, λ _k é a taxa de variação da quantidade que está sendo otimizada em função do parâmetro de restrição. Como exemplos, na mecânica Lagrangiana as equações de movimento são derivadas encontrando pontos estacionários da ação , o tempo integral da diferença entre a energia cinética e potencial. Assim, a força sobre uma partícula devido a um potencial escalar, F = −∇ V , pode ser interpretada como um multiplicador de Lagrange determinando a mudança na ação (transferência de potencial para energia cinética) seguindo uma variação na trajetória restrita da partícula. Na teoria de controle, isso é formulado como equações de custo .

Além disso, pelo teorema do envelope, o valor ótimo de um multiplicador de Lagrange tem uma interpretação como o efeito marginal da constante de restrição correspondente sobre o valor atingível ideal da função objetivo original: se denotarmos valores no ótimo com um asterisco, então ele pode ser mostrado que

${\ displaystyle {\ frac {{\ text {d}} f (x_ {1} ^ {*} (c_ {1}, c_ {2}, \ dots), x_ {2} ^ {*} (c_ { 1}, c_ {2}, \ dots), \ dots)} {{\ text {d}} c_ {k}}} = \ lambda _ {k} ^ {*}.}$

Por exemplo, em economia, o lucro ótimo para um jogador é calculado sujeito a um espaço restrito de ações, onde um multiplicador de Lagrange é a mudança no valor ótimo da função objetivo (lucro) devido ao relaxamento de uma determinada restrição (por exemplo, através uma mudança na receita); em tal contexto, λ _k * é o custo marginal da restrição e é conhecido como preço sombra .

Condições suficientes

Condições suficientes para um máximo ou mínimo local restrito podem ser declaradas em termos de uma sequência de principais menores (determinantes de submatrizes justificadas no canto superior esquerdo) da matriz Hessiana limitada de segundas derivadas da expressão Lagrangiana.

Exemplos

Exemplo 1

Ilustração do problema de otimização restrita 1a

Exemplo 1a

Suponha que desejamos maximizar o sujeito à restrição . O conjunto viável é o círculo unitário, e os conjuntos de nível de f são linhas diagonais (com inclinação -1), de modo que podemos ver graficamente que o máximo ocorre em e o mínimo em . ${\ displaystyle f (x, y) = x + y}$${\ displaystyle x ^ {2} + y ^ {2} = 1}$${\ displaystyle \ left ({\ tfrac {1} {\ sqrt {2}}}, {\ tfrac {1} {\ sqrt {2}}} \ right)}$${\ displaystyle \ left (- {\ tfrac {1} {\ sqrt {2}}}, - {\ tfrac {1} {\ sqrt {2}}} \ right)}$

Para o método dos multiplicadores de Lagrange, a restrição é

${\ displaystyle g (x, y) = x ^ {2} + y ^ {2} -1 = 0,}$

portanto

${\ displaystyle {\ begin {align} {\ mathcal {L}} (x, y, \ lambda) & = f (x, y) + \ lambda \ cdot g (x, y) \\ [4pt] & = x + y + \ lambda (x ^ {2} + y ^ {2} -1). \ end {alinhado}}}$

uma função que é equivalente a quando está definida como . ${\ displaystyle f (x, y)}$${\ displaystyle g (x, y)}$${\ displaystyle 0}$

Agora podemos calcular o gradiente:

${\ displaystyle {\ begin {alinhados} \ nabla _ {x, y, \ lambda} {\ mathcal {L}} (x, y, \ lambda) & = \ left ({\ frac {\ partial {\ mathcal { L}}} {\ parcial x}}, {\ frac {\ parcial {\ mathcal {L}}} {\ parcial y}}, {\ frac {\ parcial {\ mathcal {L}}} {\ parcial \ lambda}} \ right) \\ [4pt] & = \ left (1 + 2 \ lambda x, 1 + 2 \ lambda y, x ^ {2} + y ^ {2} -1 \ right) \ end {alinhado }}}$

e portanto:

${\ displaystyle \ nabla _ {x, y, \ lambda} {\ mathcal {L}} (x, y, \ lambda) = 0 \ quad \ Leftrightarrow \ quad {\ begin {cases} 1 + 2 \ lambda x = 0 \\ 1 + 2 \ lambda y = 0 \\ x ^ {2} + y ^ {2} -1 = 0 \ final {casos}}}$

Observe que a última equação é a restrição original.

As duas primeiras equações geram

${\ displaystyle x = y = - {\ frac {1} {2 \ lambda}}, \ qquad \ lambda \ neq 0.}$

Ao substituir na última equação, temos:

${\ displaystyle {\ frac {1} {4 \ lambda ^ {2}}} + {\ frac {1} {4 \ lambda ^ {2}}} - 1 = 0,}$

tão

${\ displaystyle \ lambda = \ pm {\ frac {1} {\ sqrt {2}}},}$

o que implica que os pontos estacionários de são ${\ displaystyle {\ mathcal {L}}}$

${\ displaystyle \ left ({\ tfrac {\ sqrt {2}} {2}}, {\ tfrac {\ sqrt {2}} {2}}, - {\ tfrac {1} {\ sqrt {2}} } \ right), \ qquad \ left (- {\ tfrac {\ sqrt {2}} {2}}, - {\ tfrac {\ sqrt {2}} {2}}, {\ tfrac {1} {\ sqrt {2}}} \ right).}$

Avaliar a função objetivo f nesses pontos resulta

${\ displaystyle f \ left ({\ tfrac {\ sqrt {2}} {2}}, {\ tfrac {\ sqrt {2}} {2}} \ right) = {\ sqrt {2}}, \ qquad f \ left (- {\ tfrac {\ sqrt {2}} {2}}, - {\ tfrac {\ sqrt {2}} {2}} \ right) = - {\ sqrt {2}}.}$

Assim, o máximo restrito é e o mínimo restrito é . ${\ displaystyle {\ sqrt {2}}}$${\ displaystyle - {\ sqrt {2}}}$

Exemplo 1b

Ilustração do problema de otimização restrita 1b

Agora modificamos a função objetivo do Exemplo 1a para que minimizemos em vez de novamente ao longo do círculo . Agora, os conjuntos de níveis de ainda são linhas de inclinação -1, e os pontos no círculo tangente a esses conjuntos de níveis são novamente e . Esses pontos de tangência são máximos de  . ${\ displaystyle f (x, y) = (x + y) ^ {2}}$${\ displaystyle f (x, y) = x + y,}$${\ displaystyle g (x, y) = x ^ {2} + y ^ {2} -1 = 0}$${\ displaystyle f}$${\ displaystyle ({\ sqrt {2}} / 2, {\ sqrt {2}} / 2)}$${\ displaystyle (- {\ sqrt {2}} / 2, - {\ sqrt {2}} / 2)}$${\ displaystyle f}$

Por outro lado, os mínimos ocorrem no nível definido para  = 0 (já que por sua construção não pode assumir valores negativos), em e , onde as curvas de nível de não são tangentes à restrição. A condição que identifica corretamente todos os quatro pontos como extremos; os mínimos são caracterizados em particular por${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle ({\ sqrt {2}} / 2, - {\ sqrt {2}} / 2)}$${\ displaystyle (- {\ sqrt {2}} / 2, {\ sqrt {2}} / 2)}$${\ displaystyle f}$${\ displaystyle \ nabla f = \ lambda \, \ nabla g}$${\ displaystyle \ lambda = 0.}$

Exemplo 2

Ilustração do problema de otimização restrita

Este exemplo lida com cálculos mais árduos, mas ainda é um problema de restrição única.

Suponha que se queira encontrar os valores máximos de

${\ displaystyle f (x, y) = x ^ {2} y}$

com a condição de que as coordenadas - e - estejam no círculo em torno da origem com raio . Ou seja, sujeito à restrição ${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle {\ sqrt {3}}}$

${\ displaystyle g (x, y) = x ^ {2} + y ^ {2} -3 = 0.}$

Como existe apenas uma única restrição, existe um único multiplicador, digamos . ${\ displaystyle \ lambda}$

A restrição é identicamente zero no círculo do raio . Qualquer múltiplo de pode ser adicionado para deixar inalterado na região de interesse (no círculo onde nossa restrição original é satisfeita). ${\ displaystyle g (x, y)}$${\ displaystyle {\ sqrt {3}}}$${\ displaystyle g (x, y)}$${\ displaystyle g (x, y)}$${\ displaystyle g (x, y)}$

A aplicação do método do multiplicador de Lagrange comum produz

${\ displaystyle {\ begin {align} {\ mathcal {L}} (x, y, \ lambda) & = f (x, y) + \ lambda \ cdot g (x, y) \\ & = x ^ { 2} y + \ lambda (x ^ {2} + y ^ {2} -3). \ End {alinhado}}}$

a partir do qual o gradiente pode ser calculado:

${\ displaystyle {\ begin {alinhado} \ nabla _ {x, y, \ lambda} {\ mathcal {L}} (x, y, \ lambda) & = \ left ({\ frac {\ partial {\ mathcal { L}}} {\ parcial x}}, {\ frac {\ parcial {\ mathcal {L}}} {\ parcial y}}, {\ frac {\ parcial {\ mathcal {L}}} {\ parcial \ lambda}} \ right) \\ & = \ left (2xy + 2 \ lambda x, x ^ {2} +2 \ lambda y, x ^ {2} + y ^ {2} -3 \ right). \ end {alinhado}}}$

E portanto:

${\ displaystyle \ nabla _ {x, y, \ lambda} {\ mathcal {L}} (x, y, \ lambda) = 0 \ quad \ iff \ quad {\ begin {cases} 2xy + 2 \ lambda x = 0 \\ x ^ {2} +2 \ lambda y = 0 \\ x ^ {2} + y ^ {2} -3 = 0 \ end {casos}} \ quad \ iff \ quad {\ begin {casos} x (y + \ lambda) = 0 & {\ text {(i)}} \\ x ^ {2} = - 2 \ lambda y & {\ text {(ii)}} \\ x ^ {2} + y ^ { 2} = 3 & {\ text {(iii)}} \ end {cases}}}$

(iii) é apenas a restrição original. (i) implica ou . Se então por (iii) e, consequentemente, por (ii). Se , substituindo isso em (ii), você obtém . Substituindo isso em (iii) e resolvendo para dá . Portanto, existem seis pontos críticos de : ${\ displaystyle x = 0}$ ${\ displaystyle \ lambda = -y}$${\ displaystyle x = 0}$${\ displaystyle y = \ pm {\ sqrt {3}}}$${\ displaystyle \ lambda = 0}$${\ displaystyle \ lambda = -y}$${\ displaystyle x ^ {2} = 2y ^ {2}}$${\ displaystyle y}$${\ displaystyle y = \ pm 1}$${\ displaystyle {\ mathcal {L}}}$

${\ displaystyle ({\ sqrt {2}}, 1, -1); \ quad (- {\ sqrt {2}}, 1, -1); \ quad ({\ sqrt {2}}, - 1, 1); \ quad (- {\ sqrt {2}}, - 1,1); \ quad (0, {\ sqrt {3}}, 0); \ quad (0, - {\ sqrt {3}} , 0).}$

Avaliando o objetivo nestes pontos, descobre-se que

${\ displaystyle f (\ pm {\ sqrt {2}}, 1) = 2; \ quad f (\ pm {\ sqrt {2}}, - 1) = - 2; \ quad f (0, \ pm { \ sqrt {3}}) = 0.}$

Portanto, a função objetivo atinge o máximo global (sujeito às restrições) em e o mínimo global em O ponto é um mínimo local de e é um máximo local de , como pode ser determinado pela consideração da matriz Hessiana de . ${\ displaystyle (\ pm {\ sqrt {2}}, 1)}$${\ displaystyle (\ pm {\ sqrt {2}}, - 1).}$${\ displaystyle (0, {\ sqrt {3}})}$${\ displaystyle f}$${\ displaystyle (0, - {\ sqrt {3}})}$${\ displaystyle f}$${\ displaystyle {\ mathcal {L}} (x, y, 0)}$

Observe que embora seja um ponto crítico de , não é um extremo local de Nós temos ${\ displaystyle ({\ sqrt {2}}, 1, -1)}$${\ displaystyle {\ mathcal {L}}}$${\ displaystyle {\ mathcal {L}}.}$

${\ displaystyle {\ mathcal {L}} \ left ({\ sqrt {2}} + \ varepsilon, 1, -1 + \ delta \ right) = 2 + \ delta \ left (\ varejpsilon ^ {2} + \ esquerda (2 {\ sqrt {2}} \ direita) \ varepsilon \ direita).}$

Dada qualquer vizinhança de , pode-se escolher um pequeno positivo e um pequeno de qualquer sinal para obter valores maiores e menores que . Isso também pode ser visto na matriz de Hessian avaliada neste ponto (ou mesmo em qualquer um dos pontos críticos), que é uma matriz indefinida . Cada um dos pontos críticos de é um ponto de sela de . ${\ displaystyle ({\ sqrt {2}}, 1, -1)}$${\ displaystyle \ varepsilon}$${\ displaystyle \ delta}$${\ displaystyle {\ mathcal {L}}}$${\ displaystyle 2}$${\ displaystyle {\ mathcal {L}}}$${\ displaystyle {\ mathcal {L}}}$${\ displaystyle {\ mathcal {L}}}$

Exemplo 3: Entropia

Suponha que desejamos encontrar a distribuição de probabilidade discreta nos pontos com entropia de informação máxima . Isso é o mesmo que dizer que desejamos encontrar a distribuição de probabilidade menos estruturada nos pontos . Em outras palavras, desejamos maximizar a equação de entropia de Shannon : ${\ displaystyle \ {p_ {1}, p_ {2}, \ ldots, p_ {n} \}}$${\ displaystyle \ {p_ {1}, p_ {2}, \ cdots, p_ {n} \}}$

${\ displaystyle f (p_ {1}, p_ {2}, \ ldots, p_ {n}) = - \ sum _ {j = 1} ^ {n} p_ {j} \ log _ {2} p_ {j }.}$

Para que esta seja uma distribuição de probabilidade, a soma das probabilidades em cada ponto deve ser igual a 1, então nossa restrição é: ${\ displaystyle p_ {i}}$${\ displaystyle x_ {i}}$

${\ displaystyle g (p_ {1}, p_ {2}, \ ldots, p_ {n}) = \ sum _ {j = 1} ^ {n} p_ {j} = 1.}$

Usamos multiplicadores de Lagrange para encontrar o ponto de entropia máxima,, em todas as distribuições de probabilidade discretas em . Exigimos que: ${\ displaystyle {\ vec {p}} ^ {\, *}}$${\ displaystyle {\ vec {p}}}$${\ displaystyle \ {x_ {1}, x_ {2}, \ ldots, x_ {n} \}}$

${\ displaystyle \ left. {\ frac {\ partial} {\ partial {\ vec {p}}}} (f + \ lambda (g-1)) \ right | _ {{\ vec {p}} = {\ vec {p}} ^ {\, *}} = 0,}$

que dá um sistema de n equações , de modo que: ${\ displaystyle k = 1, \ ldots, n}$

${\ displaystyle \ left. {\ frac {\ partial} {\ partial p_ {k}}} \ left \ {- \ left (\ sum _ {j = 1} ^ {n} p_ {j} \ log _ { 2} p_ {j} \ direita) + \ lambda \ esquerda (\ sum _ {j = 1} ^ {n} p_ {j} -1 \ direita) \ direita \} \ direita | _ {p_ {k} = p_ {k} ^ {*}} = 0.}$

Fazendo a diferenciação dessas n equações, obtemos

${\ displaystyle - \ left ({\ frac {1} {\ ln 2}} + \ log _ {2} p_ {k} ^ {*} \ right) + \ lambda = 0.}$

Isso mostra que todos são iguais (porque dependem apenas de λ ). Usando a restrição ${\ displaystyle p_ {k} ^ {*}}$

${\ displaystyle \ sum _ {j} p_ {j} = 1,}$

nós achamos

${\ displaystyle p_ {k} ^ {*} = {\ frac {1} {n}}.}$

Portanto, a distribuição uniforme é a distribuição com a maior entropia, entre as distribuições em n pontos.

Exemplo 4: Otimização numérica

Os multiplicadores de Lagrange fazem com que os pontos críticos ocorram nos pontos de sela.

A magnitude do gradiente pode ser usada para forçar os pontos críticos a ocorrerem em mínimos locais.

Os pontos críticos de Lagrangians ocorrem em pontos de sela , ao invés de máximos (ou mínimos) locais. Infelizmente, muitas técnicas de otimização numérica, como escalada , descida em gradiente , alguns dos métodos quase-Newton , entre outros, são projetadas para encontrar máximos (ou mínimos) locais e não pontos de sela. Por este motivo, deve-se modificar a formulação para garantir que seja um problema de minimização (por exemplo, extraindo o quadrado do gradiente do Lagrangiano como abaixo), ou então usar uma técnica de otimização que encontre pontos estacionários (como o método de Newton sem uma busca de linha extrema) e não necessariamente extrema.

Como um exemplo simples, considere o problema de encontrar o valor de x que minimiza , restringido de tal forma . (Este problema é um tanto patológico porque existem apenas dois valores que satisfazem esta restrição, mas é útil para fins de ilustração porque a função irrestrita correspondente pode ser visualizada em três dimensões.) ${\ displaystyle f (x) = x ^ {2}}$${\ displaystyle x ^ {2} = 1}$

Usando multiplicadores de Lagrange, este problema pode ser convertido em um problema de otimização irrestrita:

${\ displaystyle {\ mathcal {L}} (x, \ lambda) = x ^ {2} + \ lambda (x ^ {2} -1).}$

Os dois pontos críticos ocorrem em pontos de sela onde x = 1 e x = −1 .

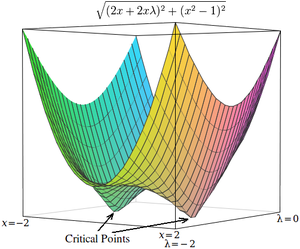
Para resolver este problema com uma técnica de otimização numérica, devemos primeiro transformar este problema de forma que os pontos críticos ocorram em mínimos locais. Isso é feito calculando a magnitude do gradiente do problema de otimização irrestrita.

Primeiro, calculamos a derivada parcial do problema irrestrito em relação a cada variável:

${\ displaystyle {\ begin {alinhados} & {\ frac {\ parcial {\ mathcal {L}}} {\ partial x}} = 2x + 2x \ lambda \\ [5pt] & {\ frac {\ partial {\ mathcal {L}}} {\ partial \ lambda}} = x ^ {2} -1. \ end {alinhado}}}$

Se a função de destino não for facilmente diferenciável, o diferencial em relação a cada variável pode ser aproximado como

${\ displaystyle {\ begin {align} {\ frac {\ partial {\ mathcal {L}}} {\ partial x}} \ approx {\ frac {{\ mathcal {L}} (x + \ varejpsilon, \ lambda) - {\ mathcal {L}} (x, \ lambda)} {\ varepsilon}}, \\ [5pt] {\ frac {\ partial {\ mathcal {L}}} {\ partial \ lambda}} \ approx { \ frac {{\ mathcal {L}} (x, \ lambda + \ varepsilon) - {\ mathcal {L}} (x, \ lambda)} {\ varejpsilon}}, \ end {alinhado}}}$

onde é um pequeno valor. ${\ displaystyle \ varepsilon}$

Em seguida, calculamos a magnitude do gradiente, que é a raiz quadrada da soma dos quadrados das derivadas parciais:

${\ displaystyle {\ begin {align} h (x, \ lambda) & = {\ sqrt {(2x + 2x \ lambda) ^ {2} + (x ^ {2} -1) ^ {2}}} \ \ [4pt] & \ approx {\ sqrt {\ left ({\ frac {{\ mathcal {L}} (x + \ varepsilon, \ lambda) - {\ mathcal {L}} (x, \ lambda)} {\ varejpsilon}} \ right) ^ {2} + \ left ({\ frac {{\ mathcal {L}} (x, \ lambda + \ varepsilon) - {\ mathcal {L}} (x, \ lambda)} { \ varejpsilon}} \ right) ^ {2}}}. \ end {alinhado}}}$

(Uma vez que a magnitude é sempre não negativa, otimizar sobre a magnitude quadrada é equivalente a otimizar sobre a magnitude. Assim, a '' raiz quadrada "pode ​​ser omitida dessas equações sem diferença esperada nos resultados da otimização.)

Os pontos críticos de h ocorrer em x = 1 e x = -1 , assim como em . Ao contrário dos pontos críticos em , no entanto, os pontos críticos em h ocorrem em mínimos locais, então técnicas de otimização numérica podem ser usadas para encontrá-los. ${\ displaystyle {\ mathcal {L}}}$${\ displaystyle {\ mathcal {L}}}$

Formulários

Teoria de controle

Na teoria de controle ótimo , os multiplicadores de Lagrange são interpretados como variáveis ​​de custo , e os multiplicadores de Lagrange são reformulados como a minimização do Hamiltoniano , no princípio do mínimo de Pontryagin .

Programação não linear

O método do multiplicador de Lagrange possui várias generalizações. Na programação não linear, existem várias regras de multiplicador, por exemplo, a Regra do Multiplicador de Carathéodory-John e a Regra do Multiplicador Convexo, para restrições de desigualdade.

Sistemas de energia

Os métodos baseados em multiplicadores de Lagrange têm aplicações em sistemas de potência , por exemplo, na colocação de recursos de energia distribuída (DER) e redução de carga.

Veja também

Referências

Leitura adicional

• Beavis, Brian; Dobbs, Ian M. (1990). "Otimização estática" . Otimização e Teoria da Estabilidade para Análise Econômica . Nova York: Cambridge University Press. pp. 32–72. ISBN 0-521-33605-8.
• Bertsekas, Dimitri P. (1982). Otimização Restrita e Métodos Multiplicadores de Lagrange . Nova York: Academic Press. ISBN 0-12-093480-9.
• Beveridge, Gordon SG; Schechter, Robert S. (1970). "Multiplicadores Lagrangianos" . Otimização: Teoria e Prática . Nova York: McGraw-Hill. pp. 244-259. ISBN 0-07-005128-3.
• Binger, Brian R .; Hoffman, Elizabeth (1998). "Otimização restrita". Microeconomics with Calculus (2ª ed.). Leitura: Addison-Wesley. pp. 56–91. ISBN 0-321-01225-9.
• Carter, Michael (2001). "Restrições de igualdade" . Fundamentos da Economia Matemática . Cambridge: MIT Press. pp. 516–549. ISBN 0-262-53192-5.
• Hestenes, Magnus R. (1966). "Mínimos de funções sujeitas a restrições de igualdade". Cálculo de Variações e Teoria de Controle Ótimo . Nova York: Wiley. pp. 29–34.
• Wylie, C. Ray; Barrett, Louis C. (1995). "O Extrema dos Integrais sob Restrição". Advanced Engineering Mathematics (Sexta ed.). Nova York: McGraw-Hill. pp. 1096-1103. ISBN 0-07-072206-4.

links externos

Exposição

• blog do kipid - Método dos multiplicadores de Lagrange
• Introdução conceitual (mais uma breve discussão dos multiplicadores de Lagrange no cálculo de variações usado na física)
• Multiplicadores de Lagrange para formas quadráticas com restrições lineares de Kenneth H. Carpenter

Para texto adicional e miniaplicativos interativos

• Explicação simples com um exemplo de governos usando impostos como multiplicadores de Lagrange
• Multiplicadores de Lagrange sem explicação de cicatriz permanente com foco na intuição de Dan Klein
• Representação geométrica do método dos multiplicadores de Lagrange Fornece uma visão convincente em 2 dimensões que, em um ponto de minimização, a direção da descida mais íngreme deve ser perpendicular à tangente da curva de restrição nesse ponto. [Precisa de InternetExplorer / Firefox / Safari] Demonstração do Mathematica por Shashi Sathyanarayana
• Applet
• MIT OpenCourseware Video Lecture on Lagrange Multipliers from Multivariable Calculus course
• Slides que acompanham o texto de otimização não linear de Bertsekas , com detalhes sobre os multiplicadores de Lagrange (aulas 11 e 12)
• Ideia geométrica por trás dos multiplicadores de Lagrange
• Exemplo MATLAB de uso de Multiplicadores Lagrange em Otimização