árvore k -d - k-d tree

árvore k -d
Uma árvore k- d tridimensional . A primeira divisão (o plano vertical vermelho) corta a célula raiz (branca) em duas subcélulas, cada uma das quais é então dividida (pelos planos horizontais verdes) em duas subcélulas. Finalmente, quatro células são divididas (pelos quatro planos verticais azuis) em duas subcélulas. Como não há mais divisão, as oito últimas são chamadas de células foliares.
Modelo	BST multidimensional
Inventado	1975
Inventado por	Jon Louis Bentley
Complexidade de tempo em notação grande O
Algoritmo Média Pior caso Espaço ${\ displaystyle O (n)}$ ${\ displaystyle O (n)}$ Procurar ${\ displaystyle O (\ log n)}$ ${\ displaystyle O (n)}$ Inserir ${\ displaystyle O (\ log n)}$ ${\ displaystyle O (n)}$ Excluir ${\ displaystyle O (\ log n)}$ ${\ displaystyle O (n)}$

Em ciência da computação , um k árvore -d (abreviação de k-dimensional da árvore ) é um de particionamento de espaço estrutura de dados para a organização de pontos em um k -dimensional espaço . As árvores k -d são uma estrutura de dados útil para várias aplicações, como pesquisas envolvendo uma chave de pesquisa multidimensional (por exemplo , pesquisas de intervalo e pesquisas de vizinho mais próximo ) e criação de nuvens de pontos . As árvores k -d são um caso especial de árvores de particionamento de espaço binário .

Descrição

A árvore k -d é uma árvore binária na qual cada nó é um ponto k- dimensional. Cada nó não folha pode ser pensado como gerando implicitamente um hiperplano de divisão que divide o espaço em duas partes, conhecidas como meios-espaços . Os pontos à esquerda desse hiperplano são representados pela subárvore esquerda desse nó e os pontos à direita do hiperplano são representados pela subárvore direita. A direção do hiperplano é escolhida da seguinte maneira: cada nó na árvore está associado a uma das k dimensões, com o hiperplano perpendicular ao eixo dessa dimensão. Assim, por exemplo, se para uma divisão particular o eixo "x" for escolhido, todos os pontos na subárvore com um valor "x" menor do que o nó aparecerão na subárvore esquerda e todos os pontos com valor "x" maior serão na subárvore certa. Nesse caso, o hiperplano seria definido pelo valor x do ponto e seu normal seria a unidade do eixo x.

Operações em árvores k -d

Construção

Como há muitas maneiras possíveis de escolher planos de divisão alinhados ao eixo, há muitas maneiras diferentes de construir árvores k -d. O método canônico de construção de árvore k -d tem as seguintes restrições:

• À medida que se desce na árvore, percorre-se os eixos usados ​​para selecionar os planos de divisão. (Por exemplo, em uma árvore tridimensional, a raiz teria um plano alinhado com x , os filhos da raiz teriam planos alinhados com y , os netos da raiz teriam todos planos alinhados com z, os bisnetos da raiz teriam todos ter planos alinhados com x, os trisnetos da raiz teriam todos planos alinhados com y e assim por diante.)
• Os pontos são inseridos selecionando a mediana dos pontos colocados na subárvore , em relação às suas coordenadas no eixo que está sendo usado para criar o plano de divisão. (Observe a suposição de que alimentamos o conjunto inteiro de n pontos no algoritmo antecipadamente.)

Este método leva a uma árvore k -d balanceada , na qual cada nó folha está aproximadamente à mesma distância da raiz. No entanto, árvores balanceadas não são necessariamente ideais para todas as aplicações.

Observe que não é necessário selecionar o ponto mediano. No caso em que os pontos medianos não são selecionados, não há garantia de que a árvore será equilibrada. Para evitar a codificação de um algoritmo de localização de mediana complexo O ( n ) ou usar uma classificação O ( n log n ) , como heapsort ou mergesort para classificar todos os n pontos, uma prática popular é classificar um número fixo de pontos selecionados aleatoriamente e usar a mediana desses pontos para servir como plano de divisão. Na prática, essa técnica geralmente resulta em árvores bem equilibradas.

Dada uma lista de n pontos, o algoritmo a seguir usa uma classificação de determinação de mediana para construir uma árvore k -d balanceada contendo esses pontos.

function kdtree (list of points pointList, int depth)
{
    // Select axis based on depth so that axis cycles through all valid values
    var int axis := depth mod k;

    // Sort point list and choose median as pivot element
    select median by axis from pointList;

    // Create node and construct subtree
    node.location := median;
    node.leftChild := kdtree(points in pointList before median, depth+1);
    node.rightChild := kdtree(points in pointList after median, depth+1);
    return node;
}

É comum que os pontos "após" a mediana incluam apenas aqueles estritamente maiores que a mediana. Para pontos que estão na mediana, é possível definir uma função "superchave" que compara os pontos em todas as dimensões. Em alguns casos, é aceitável permitir que pontos iguais à mediana fiquem em um lado da mediana, por exemplo, dividindo os pontos em um subconjunto "menor que" e um subconjunto "maior ou igual a".

Esse algoritmo cria a invariante de que, para qualquer nó, todos os nós da subárvore esquerda estão em um lado de um plano de divisão e todos os nós na subárvore direita estão do outro lado. Os pontos que se encontram no plano de divisão podem aparecer em ambos os lados. O plano de divisão de um nó passa pelo ponto associado a esse nó (referido no código como node.location ).

Algoritmos alternativos para construir uma árvore k -d balanceada pré-ordenam os dados antes de construir a árvore. Em seguida, eles mantêm a ordem da pré-classificação durante a construção da árvore e, portanto, eliminam a etapa custosa de encontrar a mediana em cada nível de subdivisão. Dois desses algoritmos constroem uma árvore k- d balanceada para classificar triângulos a fim de melhorar o tempo de execução do traçado de raio para computação gráfica tridimensional . Esses algoritmos pré-ordenam n triângulos antes de construir a árvore k- d e , em seguida, constroem a árvore em tempo O ( n log n ) no melhor caso. Um algoritmo que constrói uma árvore k -d balanceada para classificar pontos tem uma complexidade de pior caso de O ( kn log n ) . Este algoritmo pré-classifica n pontos em cada uma das k dimensões usando uma classificação O ( n log n ) , como Heapsort ou Mergesort, antes de construir a árvore. Em seguida, ele mantém a ordem dessas k pré-classificações durante a construção da árvore e, assim, evita encontrar a mediana em cada nível de subdivisão.

Implementação de exemplo

O algoritmo acima implementado na linguagem de programação Python é o seguinte:

from collections import namedtuple
from operator import itemgetter
from pprint import pformat

class Node(namedtuple("Node", "location left_child right_child")):
    def __repr__(self):
        return pformat(tuple(self))

def kdtree(point_list, depth: int = 0):
    if not point_list:
        return None

    k = len(point_list[0])  # assumes all points have the same dimension
    # Select axis based on depth so that axis cycles through all valid values
    axis = depth % k

    # Sort point list by axis and choose median as pivot element
    point_list.sort(key=itemgetter(axis))
    median = len(point_list) // 2

    # Create node and construct subtrees
    return Node(
        location=point_list[median],
        left_child=kdtree(point_list[:median], depth + 1),
        right_child=kdtree(point_list[median + 1 :], depth + 1),
    )

def main():
    """Example usage"""
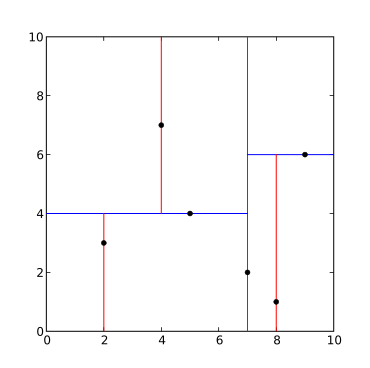
    point_list = [(7, 2), (5, 4), (9, 6), (4, 7), (8, 1), (2, 3)]
    tree = kdtree(point_list)
    print(tree)

if __name__ == "__main__":
    main()

A saída seria:

((7, 2),
 ((5, 4), ((2, 3), None, None), ((4, 7), None, None)),
 ((9, 6), ((8, 1), None, None), None))

A árvore gerada é mostrada abaixo.

decomposição da árvore k -d para o conjunto de pontos
(2,3), (5,4), (9,6), (4,7), (8,1), (7,2).

A árvore k -d resultante .

Adicionando elementos

Adiciona-se um novo ponto a uma árvore k -d da mesma forma que adiciona um elemento a qualquer outra árvore de pesquisa . Primeiro, atravesse a árvore, começando da raiz e movendo-se para a criança esquerda ou direita, dependendo se o ponto a ser inserido está no lado "esquerdo" ou "direito" do plano de divisão. Depois de chegar ao nó sob o qual o filho deve estar localizado, adicione o novo ponto como o filho esquerdo ou direito do nó folha, novamente dependendo de qual lado do plano de divisão do nó contém o novo nó.

Adicionar pontos dessa maneira pode fazer com que a árvore fique desequilibrada, levando à diminuição do desempenho da árvore. A taxa de degradação do desempenho da árvore depende da distribuição espacial dos pontos da árvore que estão sendo adicionados e do número de pontos adicionados em relação ao tamanho da árvore. Se uma árvore se tornar muito desequilibrada, pode ser necessário reequilibrá-la para restaurar o desempenho das consultas que dependem do equilíbrio da árvore, como a pesquisa do vizinho mais próximo.

Removendo elementos

Para remover um ponto de uma árvore k -d existente , sem quebrar o invariante, a maneira mais fácil é formar o conjunto de todos os nós e folhas dos filhos do nó de destino e recriar essa parte da árvore.

Outra abordagem é encontrar um substituto para o ponto removido. Primeiro, encontre o nó R que contém o ponto a ser removido. Para o caso base em que R é um nó folha, nenhuma substituição é necessária. Para o caso geral, encontre um ponto de substituição, digamos p, da subárvore enraizada em R. Substitua o ponto armazenado em R por p. Em seguida, remova recursivamente p.

Para encontrar um ponto de substituição, se R discrimina em x (digamos) e R tem um filho certo, encontre o ponto com o valor mínimo de x da subárvore enraizada no filho certo. Caso contrário, encontre o ponto com o valor máximo de x da subárvore enraizada no filho esquerdo.

Equilibrando

Equilibrar uma árvore k -d requer cuidado porque as árvores k -d são classificadas em múltiplas dimensões, então a técnica de rotação da árvore não pode ser usada para equilibrá-las, pois isso pode quebrar a invariante.

Existem várias variantes de árvores k- d balanceadas . Eles incluem árvore k -d dividida , árvore pseudo k -d, árvore KDB, árvore hB e árvore Bkd . Muitas dessas variantes são árvores kd adaptativas .

Pesquisa de vizinho mais próximo

Tocar mídia

Exemplo de pesquisa de um vizinho mais próximo em uma árvore 2-d. Aqui, a árvore já está construída, cada nó corresponde a um retângulo, cada retângulo é dividido em dois sub-retângulos iguais e as folhas correspondem a retângulos contendo um único ponto

O algoritmo de pesquisa de vizinho mais próximo (NN) visa encontrar o ponto na árvore que está mais próximo de um determinado ponto de entrada. Essa pesquisa pode ser feita de forma eficiente usando as propriedades da árvore para eliminar rapidamente grandes porções do espaço de pesquisa.

A procura de um vizinho mais próximo em uma árvore k -d procede da seguinte forma:

1. Começando com o nó raiz, o algoritmo desce na árvore recursivamente, da mesma forma que faria se o ponto de pesquisa estivesse sendo inserido (ou seja, ele vai para a esquerda ou para a direita dependendo se o ponto é menor ou maior que o nó atual em a dimensão dividida).
2. Uma vez que o algoritmo atinge um nó folha, ele verifica aquele ponto do nó e se a distância for melhor, aquele ponto do nó é salvo como o "melhor atual".
3. O algoritmo desenrola a recursão da árvore, executando as seguintes etapas em cada nó:
   1. Se o nó atual estiver mais próximo do que o melhor atual, ele se tornará o melhor atual.
   2. O algoritmo verifica se pode haver algum ponto do outro lado do plano de divisão que esteja mais próximo do ponto de busca do que o melhor atual. Conceitualmente, isso é feito cruzando o hiperplano em divisão com uma hiperesfera ao redor do ponto de busca que tem um raio igual à distância atual mais próxima. Uma vez que os hiperplanos estão todos alinhados ao eixo, isso é implementado como uma comparação simples para ver se a distância entre a coordenada de divisão do ponto de pesquisa e o nó atual é menor do que a distância (coordenadas gerais) do ponto de pesquisa ao melhor atual.
      1. Se a hiperesfera cruzar o plano, pode haver pontos mais próximos do outro lado do plano, então o algoritmo deve se mover para baixo no outro galho da árvore do nó atual procurando por pontos mais próximos, seguindo o mesmo processo recursivo de toda a pesquisa .
      2. Se a hiperesfera não interceptar o plano de divisão, o algoritmo continua subindo na árvore e todo o ramo do outro lado desse nó é eliminado.
4. Quando o algoritmo conclui esse processo para o nó raiz, a pesquisa está concluída.

Geralmente, o algoritmo usa distâncias quadradas para comparação para evitar o cálculo de raízes quadradas. Além disso, ele pode economizar computação mantendo a melhor distância quadrada da corrente em uma variável para comparação.

O algoritmo pode ser estendido de várias maneiras por meio de modificações simples. Ele pode fornecer os k vizinhos mais próximos a um ponto, mantendo k melhores atuais em vez de apenas um. Um ramo só é eliminado quando k pontos foram encontrados e o ramo não pode ter pontos mais próximos do que qualquer um dos k melhores atuais.

Ele também pode ser convertido em um algoritmo de aproximação para ser executado mais rapidamente. Por exemplo, a pesquisa aproximada do vizinho mais próximo pode ser alcançada simplesmente definindo um limite superior nos pontos de número a serem examinados na árvore, ou interrompendo o processo de pesquisa com base em um relógio de tempo real (que pode ser mais apropriado em implementações de hardware). Vizinho mais próximo para pontos que já estão na árvore pode ser alcançado não atualizando o refinamento para nós que fornecem distância zero como resultado, isso tem a desvantagem de descartar pontos que não são únicos, mas estão co-localizados com o ponto de busca original .

O vizinho mais próximo aproximado é útil em aplicações em tempo real, como robótica, devido ao aumento significativo de velocidade obtido por não pesquisar exaustivamente o melhor ponto. Uma de suas implementações é a pesquisa best-bin-first .

Pesquisa de alcance

Uma pesquisa de intervalo procura intervalos de parâmetros. Por exemplo, se uma árvore estiver armazenando valores correspondentes à renda e à idade, uma pesquisa de intervalo pode ser algo como procurar todos os membros da árvore com idade entre 20 e 50 anos e renda entre 50.000 e 80.000. Como as árvores kd dividem o intervalo de um domínio pela metade em cada nível da árvore, elas são úteis para realizar pesquisas de intervalo.

Análises de árvores de busca binária descobriu que o pior momento caso para faixa de busca é uma k -dimensional k árvore -d contendo n nós é dado pela seguinte equação.

${\ displaystyle t _ {\ text {pior}} = O \ left (k \ cdot n ^ {1 - {\ frac {1} {k}}} \ right)}$

Degradação no desempenho com dados de alta dimensão

Encontrar o ponto mais próximo é uma operação O (log n ) em média, no caso de pontos distribuídos aleatoriamente, embora a análise em geral seja complicada.

Em espaços de dimensões elevadas, a maldição da dimensionalidade faz com que o algoritmo precise visitar muito mais ramificações do que em espaços de dimensões inferiores. Em particular, quando o número de pontos é apenas ligeiramente superior ao número de dimensões, o algoritmo é apenas ligeiramente melhor do que uma pesquisa linear de todos os pontos. Como regra geral, se a dimensionalidade for k , o número de pontos nos dados, n , deve ser n ≫ 2 ^k . Caso contrário, quando árvores k -d são usadas com dados de alta dimensão, a maioria dos pontos na árvore será avaliada e a eficiência não é melhor do que uma pesquisa exaustiva e, se uma resposta suficientemente rápida for necessária, aproxime-se mais próximo métodos vizinhos devem ser usados ​​em seu lugar.

Degradação no desempenho quando o ponto de consulta está longe dos pontos na árvore k -d

Além disso, mesmo em espaço de baixa dimensão, se a distância par a par média entre os k vizinhos mais próximos do ponto de consulta for significativamente menor do que a distância média entre o ponto de consulta e cada um dos k vizinhos mais próximos, o desempenho da pesquisa de vizinho mais próximo diminui para linear, pois as distâncias do ponto de consulta a cada vizinho mais próximo são de magnitude semelhante. (No pior caso, considere uma nuvem de pontos distribuídos na superfície de uma esfera centrada na origem. Cada ponto é equidistante da origem, então uma busca pelo vizinho mais próximo da origem teria que iterar por todos os pontos no superfície da esfera para identificar o vizinho mais próximo - que neste caso nem mesmo é único.)

Para mitigar a degradação de desempenho potencialmente significativa de uma pesquisa de árvore k -d no pior caso, um parâmetro de distância máxima pode ser fornecido ao algoritmo de pesquisa de árvore, e a pesquisa recursiva pode ser podada sempre que o ponto mais próximo em um determinado ramo da árvore não pode estar mais perto do que esta distância máxima. Isso pode resultar na falha de uma pesquisa de vizinho mais próximo em retornar um vizinho mais próximo, o que significa que nenhum ponto está dentro desta distância máxima do ponto de consulta.

Complexidade

• Construir uma árvore k -d estática a partir de n pontos tem a seguinte complexidade de pior caso:
  • O ( n log ² n ) se um tipo O ( n log n ) , como Heapsort ou Mergesort, é usado para encontrar a mediana em cada nível da árvore nascente;
  • O ( n log n ) se um algoritmo de mediana de medianas O ( n ) for usado para selecionar a mediana em cada nível da árvore nascente;
  • O ( kn log n ) se n pontos forem pré-classificados em cada uma das k dimensões usando uma classificação O ( n log n ) , como Heapsort ou Mergesort antes de construir a árvore k -d .
• Inserir um novo ponto em uma árvore k -d balanceada leva tempo O (log n ) .
• Remover um ponto de uma árvore k -d balanceada leva tempo O (log n ) .
• Consultar uma faixa paralela ao eixo em uma árvore k -d balanceada leva O ( n ^{1−1 / k} + m ) tempo, onde m é o número de pontos relatados ek a dimensão da árvore k -d.
• Encontrar um vizinho mais próximo em uma árvore k- d balanceada com pontos distribuídos aleatoriamente leva um tempo O (log n ) em média.

Variações

Objetos volumétricos

Em vez de pontos, uma árvore k -d também pode conter retângulos ou hiper- retângulos . Assim, a pesquisa de alcance torna-se o problema de retornar todos os retângulos que cruzam o retângulo de pesquisa. A árvore é construída da maneira usual com todos os retângulos nas folhas. Em uma pesquisa de intervalo ortogonal , a coordenada oposta é usada na comparação com a mediana. Por exemplo, se o nível atual é dividido ao longo de x _alto , verificamos a coordenada x _baixo do retângulo de pesquisa. Se a mediana for menor do que a coordenada x _baixa do retângulo de pesquisa, nenhum retângulo no ramo esquerdo pode se cruzar com o retângulo de pesquisa e, portanto, pode ser podado. Caso contrário, ambos os ramos devem ser percorridos. Veja também a árvore de intervalo , que é um caso especial unidimensional.

Pontos apenas nas folhas

Também é possível definir uma árvore k -d com pontos armazenados apenas nas folhas. Esta forma de árvore k -d permite uma variedade de mecânicas de divisão além da divisão média padrão. A regra de divisão do ponto médio seleciona no meio do eixo mais longo do espaço que está sendo pesquisado, independentemente da distribuição dos pontos. Isso garante que a proporção da imagem será no máximo 2: 1, mas a profundidade depende da distribuição dos pontos. Uma variação, chamada de ponto médio deslizante, só se divide no meio se houver pontos em ambos os lados da divisão. Caso contrário, ele se divide no ponto mais próximo ao meio. Maneewongvatana e Mount mostram que isso oferece desempenho "bom o suficiente" em conjuntos de dados comuns.

Usando o ponto médio deslizante, uma consulta de vizinho mais próximo aproximado pode ser respondida em . A contagem de alcance aproximado pode ser respondida com este método. ${\ displaystyle O \ left ({\ tfrac {1} {{\ epsilon \} ^ {d}}} \ log n \ right)}$${\ displaystyle O \ left (\ log n + {\ left ({\ tfrac {1} {\ epsilon \}} \ right)} ^ {d} \ right)}$

Veja também

Variações aproximadas:

• árvore k -d implícita , uma árvore k -d definida por uma função de divisão implícita em vez de um conjunto de divisões armazenado explicitamente
• min / max k -d tree , uma árvore k -d que associa um valor mínimo e máximo a cada um de seus nós
• Árvore k -d relaxada , uma árvore k -d em que os discriminantes em cada nó são arbitrários

Variações relacionadas:

• Quadtree , uma estrutura de partição de espaço que se divide em duas dimensões simultaneamente, de modo que cada nó tem 4 filhos
• Octree , uma estrutura de partição do espaço que se divide em três dimensões simultaneamente, de modo que cada nó tem 8 filhos
• Ball tree , um particionamento de espaço multidimensional útil para a pesquisa do vizinho mais próximo
• Árvore R e hierarquia de intervalo delimitador , estrutura para objetos de particionamento em vez de pontos, com regiões sobrepostas
• Árvore de ponto de vista , uma variante de uma árvore k -d que usa hiperesferas em vez de hiperplanos para particionar os dados

Problemas que podem ser resolvidos com árvores k -d:

• Particionamento recursivo , uma técnica para construir árvores de decisão estatísticas semelhantes às árvores k -d
• O problema de medição de Klee , um problema de cálculo da área de uma união de retângulos, solucionável usando árvores k -d
• Problema de guilhotina , um problema de encontrar uma árvore k -d cujas células são grandes o suficiente para conter um determinado conjunto de retângulos

Implementações de código aberto

• ALGLIB tem implementações em C # e C ++ de algoritmos de vizinho mais próximo baseado em árvore k -d e vizinho mais próximo aproximado
• SciPy , uma biblioteca Python para computação científica, contém implementações de algoritmos de pesquisa de vizinho mais próximo baseados em árvore k -d.
• scikit-learn , uma biblioteca Python para aprendizado de máquina, contém implementações de árvores k -d para dar suporte a pesquisas de vizinho mais próximo e vizinho de raio.

Referências