Paridade (física) - Parity (physics)

Na mecânica quântica , uma transformação de paridade (também chamada de inversão de paridade ) é a mudança no sinal de uma coordenada espacial . Em três dimensões, também pode se referir à inversão simultânea no sinal de todas as três coordenadas espaciais (um ponto de reflexão ):

${\ displaystyle \ mathbf {P}: {\ begin {pmatrix} x \\ y \\ z \ end {pmatrix}} \ mapsto {\ begin {pmatrix} -x \\ - y \\ - z \ end {pmatrix }}.}$

Também pode ser pensado como um teste de quiralidade de um fenômeno físico, em que uma inversão de paridade transforma um fenômeno em sua imagem no espelho. Todas as interações fundamentais de partículas elementares , com exceção da interação fraca , são simétricas sob paridade. A interação fraca é quiral e, portanto, fornece um meio para investigar a quiralidade em física. Em interações simétricas sob paridade, como o eletromagnetismo na física atômica e molecular, a paridade serve como um poderoso princípio de controle subjacente às transições quânticas.

Uma representação de matriz de P (em qualquer número de dimensões) tem determinante igual a −1 e, portanto, é distinta de uma rotação , que tem um determinante igual a 1. Em um plano bidimensional, uma inversão simultânea de todas as coordenadas no sinal não é uma transformação de paridade; é o mesmo que uma rotação de 180 ° .

Na mecânica quântica , as funções de onda que não são alteradas por uma transformação de paridade são descritas como funções pares , enquanto aquelas que mudam de sinal sob uma transformação de paridade são funções ímpares.

Relações de simetria simples

Sob rotações , objetos geométricos clássicos podem ser classificados em escalares , vetores e tensores de classificação superior. Na física clássica , as configurações físicas precisam se transformar em representações de todos os grupos de simetria.

A teoria quântica prevê que os estados em um espaço de Hilbert não precisam se transformar sob representações do grupo de rotações, mas apenas sob representações projetivas . A palavra projetiva refere-se ao fato de que se projetarmos a fase de cada estado, onde lembramos que a fase geral de um estado quântico não é observável, então uma representação projetiva se reduz a uma representação comum. Todas as representações também são representações projetivas, mas o inverso não é verdadeiro, portanto a condição de representação projetiva nos estados quânticos é mais fraca do que a condição de representação nos estados clássicos.

As representações projetivas de qualquer grupo são isomórficas às representações comuns de uma extensão central do grupo. Por exemplo, representações projetivas do grupo de rotação tridimensional, que é o grupo ortogonal especial SO (3), são representações ordinárias do grupo unitário especial SU (2) (ver Teoria de representação de SU (2) ). As representações projetivas do grupo de rotação que não são representações são chamadas de espinores e, portanto, os estados quânticos podem se transformar não apenas como tensores, mas também como espinores.

Se adicionarmos a isso uma classificação por paridade, estes podem ser estendidos, por exemplo, em noções de

• escalares ( P = +1 ) e pseudoescalares ( P = −1 ) que são rotacionalmente invariantes.
• vetores ( P = −1 ) e vetores axiais (também chamados de pseudovetores ) ( P = +1 ) que se transformam em vetores sob rotação.

Pode-se definir reflexos como

${\ displaystyle V_ {x}: {\ begin {pmatrix} x \\ y \\ z \ end {pmatrix}} \ mapsto {\ begin {pmatrix} -x \\ y \\ z \ end {pmatrix}}, }$

que também têm determinante negativo e formam uma transformação de paridade válida. Então, combinando-as com rotações (ou realizando sucessivamente reflexões x -, y - e z ), pode-se recuperar a transformação de paridade específica definida anteriormente. A primeira transformação de paridade fornecida não funciona em um número par de dimensões, porém, porque resulta em um determinante positivo. Em dimensões pares, apenas o último exemplo de uma transformação de paridade (ou qualquer reflexão de um número ímpar de coordenadas) pode ser usado.

A paridade forma o grupo abeliano devido à relação . Todos os grupos Abelianos têm apenas representações irredutíveis unidimensionais . Pois , há duas representações irredutíveis: uma é par em paridade , a outra é ímpar ,. Eles são úteis na mecânica quântica . No entanto, como é elaborado abaixo, na mecânica quântica os estados não precisam se transformar sob representações reais de paridade, mas apenas sob representações projetivas e, portanto, em princípio, uma transformação de paridade pode girar um estado em qualquer fase . ${\ displaystyle \ mathbb {Z} _ {2}}$${\ displaystyle {\ hat {\ mathcal {P}}} ^ {2} = {\ hat {1}}}$${\ displaystyle \ mathbb {Z} _ {2}}$${\ displaystyle {\ hat {\ mathcal {P}}} \ phi = + \ phi}$${\ displaystyle {\ hat {\ mathcal {P}}} \ phi = - \ phi}$

Mecânica clássica

A equação de movimento de Newton (se a massa for constante) equivale a dois vetores e, portanto, é invariante sob paridade. A lei da gravidade também envolve apenas vetores e também é, portanto, invariante sob a paridade. ${\ displaystyle \ mathbf {F} = m \ mathbf {a}}$

No entanto, o momento angular é um vetor axial , ${\ displaystyle \ mathbf {L}}$

${\ displaystyle {\ begin {alinhados} \ mathbf {L} & = \ mathbf {r} \ times \ mathbf {p} \\ {\ hat {P}} \ left (\ mathbf {L} \ right) & = (- \ mathbf {r}) \ times (- \ mathbf {p}) = \ mathbf {L}. \ end {alinhado}}}$

Na eletrodinâmica clássica , a densidade de carga é um escalar, o campo elétrico , e a corrente são vetores, mas o campo magnético é um vetor axial. No entanto, as equações de Maxwell são invariantes sob paridade porque a curvatura de um vetor axial é um vetor. ${\ displaystyle \ rho}$${\ displaystyle \ mathbf {E}}$${\ displaystyle \ mathbf {j}}$${\ displaystyle \ mathbf {B}}$

Efeito da inversão espacial em algumas variáveis ​​da física clássica

As duas principais divisões das variáveis ​​físicas clássicas têm paridade par ou ímpar. A maneira pela qual variáveis ​​e vetores específicos se classificam em qualquer uma das categorias depende se o número de dimensões do espaço é ímpar ou par. As categorias de ímpar ou par fornecidas abaixo para a transformação de paridade são uma questão diferente, mas intimamente relacionada.

As respostas fornecidas abaixo estão corretas para 3 dimensões espaciais. Em um espaço bidimensional, por exemplo, quando restringido para permanecer na superfície de um planeta, algumas das variáveis ​​mudam de lado.

Ímpar

Variáveis ​​clássicas cujos sinais mudam quando invertidos na inversão do espaço são predominantemente vetores. Eles incluem:

Até

Variáveis ​​clássicas, quantidades predominantemente escalares, que não mudam com a inversão espacial incluem:

Mecânica quântica

Autovalores possíveis

As representações bidimensionais de paridade são fornecidas por um par de estados quânticos que se inserem em paridade. No entanto, essa representação sempre pode ser reduzida a combinações lineares de estados, cada um dos quais é par ou ímpar em paridade. Diz-se que todas as representações irredutíveis de paridade são unidimensionais.

Na mecânica quântica , as transformações do espaço-tempo atuam nos estados quânticos . A transformação de paridade, , é um operador unitária , em geral, agindo sobre um estado como se segue: . ${\ displaystyle {\ hat {\ mathcal {P}}}}$${\ displaystyle \ psi}$${\ displaystyle {\ hat {\ mathcal {P}}} \, \ psi {\ left (r \ right)} = e ^ {\ frac {i \ phi} {2}} \ psi {\ left (-r \direito)}}$

Deve-se então ter , uma vez que uma fase geral não é observável. O operador , que inverte a paridade de um estado duas vezes, deixa o espaço-tempo invariante e, portanto, é uma simetria interna que gira seus estados próprios por fases . Se for um elemento de um grupo de simetria contínua U (1) de rotações de fase, então faz parte desse U (1) e, portanto, também é uma simetria. Em particular, podemos definir , que também é uma simetria, e então podemos escolher chamar nosso operador de paridade, em vez de . Observe que e assim tem autovalores . As funções de onda com valor próprio +1 sob uma transformação de paridade são funções pares , enquanto o valor próprio -1 corresponde a funções ímpares. No entanto, quando não existe tal grupo de simetria, pode ser que todas as transformações de paridade tenham alguns valores próprios que são fases diferentes de . ${\ displaystyle {\ hat {\ mathcal {P}}} ^ {2} \, \ psi {\ left (r \ right)} = e ^ {i \ phi} \ psi {\ left (r \ right)} }$${\ displaystyle {\ hat {\ mathcal {P}}} ^ {2}}$${\ displaystyle e ^ {i \ phi}}$${\ displaystyle {\ hat {\ mathcal {P}}} ^ {2}}$${\ displaystyle e ^ {iQ}}$${\ displaystyle e ^ {- iQ}}$${\ displaystyle {\ hat {\ mathcal {P}}} '\ equiv {\ hat {\ mathcal {P}}} \, e ^ {- {iQ} / {2}}}$${\ displaystyle {\ hat {\ mathcal {P}}} '}$${\ displaystyle {\ hat {\ mathcal {P}}}}$${\ displaystyle {{\ hat {\ mathcal {P}}} '} ^ {2} = 1}$${\ displaystyle {\ hat {\ mathcal {P}}} '}$${\ displaystyle \ pm 1}$${\ displaystyle \ pm 1}$

Para funções de onda eletrônicas, os estados pares são geralmente indicados por um subscrito g para gerade (alemão: par) e os estados ímpares por um subscrito u para ungerade (alemão: ímpar). Por exemplo, o nível de energia mais baixo do íon da molécula de hidrogênio (H ₂ ⁺ ) é rotulado e o nível de energia mais próximo (mais alto) é rotulado . ${\ displaystyle 1 \ sigma _ {g}}$${\ displaystyle 1 \ sigma _ {u}}$

As funções de onda de uma partícula movendo-se para um potencial externo, que é centrosimétrico (energia potencial invariante em relação a uma inversão espacial, simétrica à origem), ou permanecem invariáveis ​​ou mudam de sinal: esses dois estados possíveis são chamados de estado par ou ímpar estado das funções de onda.

A lei da conservação da paridade da partícula (não é verdade para o decaimento beta dos núcleos) afirma que, se um conjunto isolado de partículas tem uma paridade definida, então a paridade permanece invariável no processo de evolução do conjunto.

A paridade dos estados de uma partícula se movendo em um campo externo esfericamente simétrico é determinada pelo momento angular , e o estado da partícula é definido por três números quânticos: energia total, momento angular e a projeção do momento angular.

Consequências da simetria de paridade

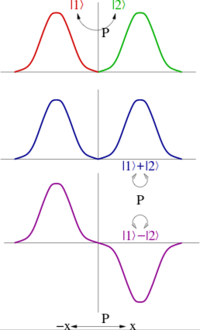
Quando a paridade gera o grupo Abeliano ℤ ₂ , pode-se sempre tomar combinações lineares de estados quânticos de modo que sejam pares ou ímpares sob paridade (veja a figura). Portanto, a paridade de tais estados é ± 1. A paridade de um estado de multipartículas é o produto das paridades de cada estado; em outras palavras, a paridade é um número quântico multiplicativo.

Na mecânica quântica, os hamiltonianos são invariantes (simétricos) sob uma transformação de paridade se comuta com o hamiltoniano. Na mecânica quântica não relativística , isso acontece para qualquer potencial escalar, ou seja , portanto, o potencial é esfericamente simétrico. Os seguintes fatos podem ser facilmente comprovados: ${\ displaystyle {\ hat {\ mathcal {P}}}}$ ${\ displaystyle V = V {\ left (r \ right)}}$

• Se e tiver a mesma paridade, onde está o operador de posição .${\ displaystyle \ left | \ varphi \ right \ rangle}$${\ displaystyle \ left | \ psi \ right \ rangle}$${\ displaystyle \ left \ langle \ varphi \ left | {\ hat {X}} \ right | \ psi \ right \ rangle = 0}$${\ displaystyle {\ hat {X}}}$
• Para um estado de momento angular orbital com projeção no eixo z , então .${\ displaystyle \ left | {\ vec {L}}, L_ {z} \ right \ rangle}$${\ displaystyle {\ vec {L}}}$${\ displaystyle L_ {z}}$${\ displaystyle {\ hat {\ mathcal {P}}} \ left | {\ vec {L}}, L_ {z} \ right \ rangle = \ left (-1 \ right) ^ {L} \ left | { \ vec {L}}, L_ {z} \ right \ rangle}$
• Se , então, as transições dipolo atômicas ocorrem apenas entre estados de paridade oposta.${\ displaystyle \ left [{\ hat {H}}, {\ hat {P}} \ right] = 0}$
• Se , então, um estado próprio não degenerado de também é um estado próprio do operador de paridade; isto é, uma autofunção não degenerada de é invariante para ou tem seu sinal alterado por .${\ displaystyle \ left [{\ hat {H}}, {\ hat {P}} \ right] = 0}$${\ displaystyle {\ hat {H}}}$${\ displaystyle {\ hat {H}}}$${\ displaystyle {\ hat {\ mathcal {P}}}}$${\ displaystyle {\ hat {\ mathcal {P}}}}$

Algumas das autofunções não degeneradas de não são afetadas (invariantes) pela paridade e as outras são meramente invertidas no sinal quando o operador hamiltoniano e o operador de paridade comutam : ${\ displaystyle {\ hat {H}}}$${\ displaystyle {\ hat {\ mathcal {P}}}}$

${\ displaystyle {\ hat {\ mathcal {P}}} \ left | \ psi \ right \ rangle = c \ left | \ psi \ right \ rangle,}$

onde é uma constante, o autovalor de , ${\ displaystyle c}$${\ displaystyle {\ hat {\ mathcal {P}}}}$

${\ displaystyle {\ hat {\ mathcal {P}}} ^ {2} \ left | \ psi \ right \ rangle = c \, {\ hat {\ mathcal {P}}} \ left | \ psi \ right \ rangle.}$

Sistemas de muitas partículas: átomos, moléculas, núcleos

A paridade geral de um sistema de muitas partículas é o produto das paridades dos estados de uma partícula. É -1 se um número ímpar de partículas estiver em estados de paridade ímpar e +1 caso contrário. Diferentes notações são usadas para denotar a paridade de núcleos, átomos e moléculas.

Átomos

Orbitais atômicos têm paridade (−1) ^ℓ , onde o expoente ℓ é o número quântico azimutal . A paridade é ímpar para os orbitais p, f, ... com ℓ = 1, 3, ..., e um estado atômico tem paridade ímpar se um número ímpar de elétrons ocupar esses orbitais. Por exemplo, o estado fundamental do átomo de nitrogênio tem a configuração eletrônica 1s ² 2s ² 2p ³ e é identificado pelo símbolo de termo ⁴ S ^o , onde o sobrescrito o denota paridade ímpar. No entanto, o terceiro termo excitado em cerca de 83.300 cm ⁻¹ acima do estado fundamental tem configuração de elétron 1s ² 2s ² 2p ² 3s tem paridade uniforme, uma vez que há apenas dois elétrons 2p, e seu símbolo de termo é ⁴ P (sem um sobrescrito o).

Moléculas

O hamiltoniano eletromagnético completo (spin rotacional-vibracional-eletrônico-nuclear) de qualquer molécula comuta com (ou é invariante) a operação de paridade P (ou E *, na notação introduzida por Longuet-Higgins ) e seus autovalores podem ser dados a etiqueta de simetria de paridade + ou - visto que são pares ou ímpares, respectivamente. A operação de paridade envolve a inversão das coordenadas espaciais eletrônicas e nucleares no centro de massa molecular.

As moléculas centrossimétricas em equilíbrio têm um centro de simetria em seu ponto médio (o centro nuclear de massa). Isso inclui todas as moléculas diatômicas homonucleares , bem como certas moléculas simétricas, como etileno , benzeno , tetrafluoreto de xenônio e hexafluoreto de enxofre . Para moléculas centrosimétricas, o grupo de pontos contém a operação i, que não deve ser confundida com a operação de paridade. A operação i envolve a inversão das coordenadas de deslocamento eletrônico e vibracional no centro de massa nuclear. Para moléculas centrosimétricas, a operação i comuta com o hamiltoniano rovibrônico (rotação-vibração-eletrônico) e pode ser usada para rotular tais estados. Os estados eletrônicos e vibracionais das moléculas centrossimétricas não são alterados pela operação i , ou seus sinais são alterados por i . Os primeiros são denotados pelo subscrito ge são chamados de gerade, enquanto os últimos são denotados pelo subscrito u e são chamados de ungerade. O hamiltoniano completo de uma molécula centrosimétrica não comuta com a operação de inversão do grupo de pontos i devido ao efeito do hamiltoniano hiperfino nuclear. O hiperfina nuclear Hamiltoniano pode misturar os níveis de rotação de g e u estados vibrônicas (chamados orto - para mistura) e dar origem a orto - para- transições

Núcleos

Em núcleos atômicos, o estado de cada nucleon (próton ou nêutron) tem paridade par ou ímpar, e as configurações do nucleon podem ser previstas usando o modelo de camada nuclear . Quanto aos elétrons nos átomos, o estado do núcleo tem paridade geral ímpar se e somente se o número de núcleos nos estados de paridade ímpar for ímpar. A paridade é geralmente escrita como + (par) ou - (ímpar) após o valor de spin nuclear. Por exemplo, os isótopos de oxigênio incluem ¹⁷ O (5/2 +), o que significa que o spin é 5/2 e a paridade é par. O modelo de casca explica isso porque os primeiros 16 núcleos são emparelhados de modo que cada par tenha spin zero e paridade par, e o último nucleon está na camada 1d _5/2 , que tem paridade par, uma vez que ℓ = 2 para orbital ad.

Teoria quântica de campos

As atribuições de paridade intrínseca nesta seção são verdadeiras para a mecânica quântica relativística, bem como para a teoria quântica de campos.

Se pudermos mostrar que o estado de vácuo é invariante em paridade, o hamiltoniano é invariante em paridade e as condições de quantização permanecem inalteradas em paridade, então segue-se que todo estado tem boa paridade, e essa paridade é conservada em qualquer reação. ${\ displaystyle {\ hat {\ mathcal {P}}} \ left | 0 \ right \ rangle = \ left | 0 \ right \ rangle}$${\ displaystyle \ left [{\ hat {H}}, {\ hat {\ mathcal {P}}} \ right]}$

Para mostrar que a eletrodinâmica quântica é invariante sob paridade, temos que provar que a ação é invariante e a quantização também é invariante. Para simplificar, assumiremos que a quantização canônica é usada; o estado de vácuo é então invariante em paridade por construção. A invariância da ação segue da invariância clássica das equações de Maxwell. A invariância do procedimento de quantização canônica pode ser calculada e acaba dependendo da transformação do operador de aniquilação:

Pa ( p , ±) P ⁺  = - a (- p , ±)

onde p denota o momento de um fóton e ± refere-se ao seu estado de polarização. Isso é equivalente à afirmação de que o fóton tem paridade intrínseca ímpar . Da mesma forma, todos os bósons de vetor podem ter paridade intrínseca ímpar e todos os vetores axiais têm paridade intrínseca par.

Uma extensão direta desses argumentos às teorias de campo escalar mostra que os escalares têm paridade uniforme, uma vez que

Pa ( p ) P ⁺  =  a (- p ).

Isso é verdade mesmo para um campo escalar complexo. (Os detalhes dos espinores são tratados no artigo sobre a equação de Dirac , onde é mostrado que os férmions e os antifermions têm paridade intrínseca oposta. )

Com férmions , há uma pequena complicação porque há mais de um grupo de spin .

Paridade no modelo padrão

Corrigindo as simetrias globais

No modelo padrão de interações fundamentais há precisamente três interna globais U (1) grupos de simetria disponíveis, com encargos equivalentes a baryon número B , o lepton número L ea carga elétrica Q . O produto do operador de paridade com qualquer combinação dessas rotações é outro operador de paridade. É convencional escolher uma combinação específica dessas rotações para definir um operador de paridade padrão, e outros operadores de paridade são relacionados ao padrão por rotações internas. Uma maneira de fixar um operador de paridade padrão é atribuir as paridades de três partículas com cargas B , L e Q linearmente independentes . Em geral, atribui-se a paridade das partículas massivas mais comuns, o próton , o nêutron e o elétron , como +1.

Steven Weinberg mostrou que se P ² = (−1) ^F , onde F é o operador do número do férmion , então, uma vez que o número do férmion é a soma do número do leptão mais o número do bárion, F = B + L , para todas as partículas no Modelo Padrão e como o número de leptões e o número de bárions são cargas Q de simetrias contínuas e ^iQ , é possível redefinir o operador de paridade para que P ² = 1 . No entanto, se existem neutrinos de Majorana , que os experimentalistas hoje acreditam ser possível, seu número de férmions é igual a um porque eles são neutrinos, enquanto seus números de bárions e leptões são zero porque eles são de Majorana, e assim (-1) ^F não seria incorporado em um grupo de simetria contínua. Assim, os neutrinos de Majorana teriam paridade ± i .

Paridade do píon

Em 1954, um artigo de William Chinowsky e Jack Steinberger demonstrou que o píon tem paridade negativa. Eles estudaram a decomposição de um "átomo" feito de um deutério (²
₁H⁺
) e um píon carregado negativamente (
π^-
) em um estado com momento angular orbital zero em dois nêutrons ( ). ${\ displaystyle ~ \ mathbf {L} = {\ boldsymbol {0}} ~}$${\ displaystyle n}$

Os nêutrons são férmions e, portanto, obedecem às estatísticas de Fermi-Dirac , o que implica que o estado final é antissimétrico. Usando o fato de que o deutério tem spin um e o píon spin zero juntamente com a antissimetria do estado final, eles concluíram que os dois nêutrons devem ter momento angular orbital. A paridade total é o produto das paridades intrínsecas das partículas e da paridade extrínseca. da função harmônica esférica Uma vez que o momento orbital muda de zero para um neste processo, se o processo deve conservar a paridade total, então os produtos das paridades intrínsecas das partículas inicial e final devem ter sinal oposto. Um núcleo deutério é feito de um próton e um nêutron e, portanto, usando a convenção mencionada de que prótons e nêutrons têm paridades intrínsecas iguais a eles argumentaram que a paridade do píon é igual a menos o produto das paridades dos dois nêutrons dividido por a do próton e do nêutron no deutério, explicitamente a partir da qual eles concluíram que o píon é uma partícula pseudoescalar . ${\ displaystyle ~ L = 1 ~.}$${\ displaystyle ~ \ left (-1 \ right) ^ {L} ~.}$${\ displaystyle ~ + 1 ~}$${\ textstyle {\ frac {(-1) (1) ^ {2}} {(1) ^ {2}}} = - 1 ~,}$

Violação de paridade

Acima: Simetria P: um relógio construído como sua imagem espelhada se comporta como a imagem espelhada do relógio original.

Abaixo: P- uma simetria: Um relógio construído como sua imagem espelhada que não se comporta como uma imagem espelhada do relógio original.

Embora a paridade seja conservada no eletromagnetismo , nas interações fortes e na gravidade , ela é violada nas interações fracas . O modelo padrão incorpora violação de paridade , expressando a interação fraca como uma interação de medidor quiral . Apenas os componentes canhotos das partículas e os componentes destros das antipartículas participam de interações fracas carregadas no Modelo Padrão . Isso implica que a paridade não é uma simetria de nosso universo, a menos que exista um setor de espelho oculto no qual a paridade seja violada de maneira oposta.

Um obscuro experimento de 1928, feito por RT Cox , GC McIlwraith e B. Kurrelmeyer, havia relatado violação de paridade em decaimentos fracos , mas uma vez que os conceitos apropriados ainda não haviam sido desenvolvidos, esses resultados não tiveram impacto. Em 1929, Hermann Weyl explorou, sem qualquer evidência, a existência de uma partícula sem massa de dois componentes de spin meio. Essa ideia foi rejeitada por Pauli, pois implicava violação da paridade.

Em meados do século 20, vários cientistas sugeriram que a paridade poderia não ser conservada (em contextos diferentes), mas sem evidências sólidas essas sugestões não eram consideradas importantes. Então, em 1956, uma cuidadosa revisão e análise pelos físicos teóricos Tsung-Dao Lee e Chen-Ning Yang foram além, mostrando que, embora a conservação da paridade tenha sido verificada em decaimentos pelas interações fortes ou eletromagnéticas , não foi testada na interação fraca . Eles propuseram vários testes experimentais diretos possíveis. Quase todos foram ignorados, mas Lee conseguiu convencer seu colega de Columbia, Chien-Shiung Wu, a tentar. Ela precisava de instalações criogênicas especiais e experiência, então o experimento foi feito no National Bureau of Standards .

Wu , Ambler , Hayward, Hoppes e Hudson (1957) encontraram uma violação clara da conservação da paridade na decadência beta do cobalto-60 . À medida que o experimento estava terminando, com uma dupla verificação em andamento, Wu informou Lee e Yang de seus resultados positivos e, dizendo que os resultados precisavam de um exame mais aprofundado, ela pediu a eles que não publicassem os resultados primeiro. No entanto, Lee revelou os resultados a seus colegas de Columbia em 4 de janeiro de 1957 em um encontro de "almoço de sexta-feira" do Departamento de Física de Columbia. Três deles, RL Garwin , LM Lederman e RM Weinrich modificaram um experimento de ciclotron existente e verificaram imediatamente a violação de paridade. Eles atrasaram a publicação de seus resultados até depois que o grupo de Wu estivesse pronto, e os dois artigos apareceram consecutivamente no mesmo periódico de física.

A descoberta da violação de paridade explicou imediatamente o notável quebra - cabeça τ – θ na física dos kaons .

Em 2010, foi relatado que os físicos trabalhando com o Relativistic Heavy Ion Collider (RHIC) criaram uma bolha de quebra de simetria de paridade de curta duração em plasmas quark-gluon . Um experimento conduzido por vários físicos na colaboração STAR , sugeriu que a paridade também pode ser violada na interação forte. Prevê-se que esta violação da paridade local, que seria análogo ao efeito que é induzido pela flutuação do campo axion , se manifeste por efeito magnético quiral .

Paridade intrínseca de hádrons

A cada partícula pode-se atribuir uma paridade intrínseca , desde que a natureza preserve a paridade. Embora as interações fracas não o façam, ainda se pode atribuir uma paridade a qualquer hádron examinando a forte reação de interação que a produz, ou por decaimentos que não envolvem a interação fraca , como o decaimento do meson rho para píons .

Veja também

• Simetria molecular
• Teoria eletrofraca
• Modelo Padrão
• Violação de CP
• Matéria espelho
• Simetria T
• Simetria C

Referências

Em geral

• Perkins, Donald H. (2000). Introdução à Física de Altas Energias . ISBN 9780521621960.
• Sozzi, MS (2008). Simetrias discretas e violação de CP . Oxford University Press . ISBN 978-0-19-929666-8.
• Bigi, II; Sanda, AI (2000). Violação de CP . Cambridge Monographs on Particle Physics, Nuclear Physics and Cosmology. Cambridge University Press . ISBN 0-521-44349-0.
• Weinberg, S. (1995). The Quantum Theory of Fields . Cambridge University Press . ISBN 0-521-67053-5.

Específico