óptica -Optics

Um pesquisador trabalhando em um sistema óptico

Parte de uma série sobre
Física
A ciência fundamental
Índice Contorno Glossário História ( linha do tempo )
Galhos Acústica Astrofísica física atômica Biofísica física clássica Eletromagnetismo Geofísica Mecânica física moderna Física nuclear óptica Termodinâmica
Pesquisar Físico ( lista ) Lista de prêmios de física Lista de revistas Lista de problemas não resolvidos
portal de física  Categoria
v t e

A óptica é o ramo da física que estuda o comportamento e as propriedades da luz , incluindo suas interações com a matéria e a construção de instrumentos que a utilizam ou detectam . A óptica geralmente descreve o comportamento da luz visível , ultravioleta e infravermelha . Como a luz é uma onda eletromagnética , outras formas de radiação eletromagnética , como raios X , micro-ondas e ondas de rádio , exibem propriedades semelhantes.

A maioria dos fenômenos ópticos pode ser explicada usando a descrição eletromagnética clássica da luz, no entanto descrições eletromagnéticas completas da luz são muitas vezes difíceis de aplicar na prática. A óptica prática geralmente é feita usando modelos simplificados. A mais comum delas, a óptica geométrica , trata a luz como uma coleção de raios que viajam em linhas retas e se dobram quando passam ou refletem em superfícies. A ótica física é um modelo mais abrangente de luz, que inclui efeitos de onda , como difração e interferência , que não podem ser contabilizados na ótica geométrica. Historicamente, o modelo de luz baseado em raios foi desenvolvido primeiro, seguido pelo modelo de onda de luz. O progresso na teoria eletromagnética no século 19 levou à descoberta de que as ondas de luz eram de fato radiação eletromagnética.

Alguns fenômenos dependem da luz ter propriedades semelhantes a ondas e partículas . A explicação desses efeitos requer a mecânica quântica . Ao considerar as propriedades de partículas da luz, a luz é modelada como uma coleção de partículas chamadas " fótons ". A óptica quântica lida com a aplicação da mecânica quântica a sistemas ópticos.

A ciência óptica é relevante e estudada em muitas disciplinas relacionadas, incluindo astronomia , vários campos da engenharia , fotografia e medicina (particularmente oftalmologia e optometria , nas quais é chamada de óptica fisiológica). As aplicações práticas da óptica são encontradas em uma variedade de tecnologias e objetos do cotidiano, incluindo espelhos , lentes , telescópios , microscópios , lasers e fibras ópticas .

História

A lente de Nimrud

A óptica começou com o desenvolvimento de lentes pelos antigos egípcios e mesopotâmios . As primeiras lentes conhecidas, feitas de cristal polido, muitas vezes quartzo , datam de 2000 aC de Creta (Museu Arqueológico de Heraclion, Grécia). As lentes de Rodes datam de cerca de 700 aC, assim como as lentes assírias , como a lente de Nimrud . Os antigos romanos e gregos enchiam esferas de vidro com água para fazer lentes. Esses desenvolvimentos práticos foram seguidos pelo desenvolvimento de teorias de luz e visão pelos antigos filósofos gregos e indianos , e pelo desenvolvimento da óptica geométrica no mundo greco-romano . A palavra óptica vem da antiga palavra grega ὀπτική ( optikē ), que significa "aparência, olhar".

A filosofia grega sobre óptica se dividiu em duas teorias opostas sobre como a visão funcionava, a teoria da intromissão e a teoria da emissão . A abordagem de intromissão via a visão como proveniente de objetos lançando cópias de si mesmos (chamados eidola) que foram capturados pelo olho. Com muitos propagadores, incluindo Demócrito , Epicuro , Aristóteles e seus seguidores, essa teoria parece ter algum contato com as teorias modernas sobre o que a visão realmente é, mas permaneceu apenas especulação sem qualquer fundamento experimental.

Platão primeiro articulou a teoria da emissão, a ideia de que a percepção visual é realizada por raios emitidos pelos olhos. Ele também comentou sobre a inversão de paridade dos espelhos no Timeu . Algumas centenas de anos depois, Euclides (século IV-III aC) escreveu um tratado intitulado Óptica , onde ligou a visão à geometria , criando a óptica geométrica . Ele baseou seu trabalho na teoria da emissão de Platão, na qual descreveu as regras matemáticas da perspectiva e descreveu os efeitos da refração qualitativamente, embora questionasse que um feixe de luz do olho poderia iluminar instantaneamente as estrelas toda vez que alguém piscasse. Euclides declarou o princípio da trajetória mais curta da luz e considerou reflexões múltiplas em espelhos planos e esféricos. Ptolomeu , em seu tratado Óptica , sustentava uma teoria da visão de extramissão-intromissão: os raios (ou fluxo) do olho formavam um cone, o vértice estando dentro do olho e a base definindo o campo visual. Os raios eram sensíveis e transmitiam informações ao intelecto do observador sobre a distância e a orientação das superfícies. Ele resumiu muito de Euclides e passou a descrever uma maneira de medir o ângulo de refração , embora não tenha percebido a relação empírica entre ele e o ângulo de incidência. Plutarco (século I-II dC) descreveu reflexões múltiplas em espelhos esféricos e discutiu a criação de imagens ampliadas e reduzidas, tanto reais quanto imaginárias, incluindo o caso da quiralidade das imagens.

Reprodução de uma página do manuscrito de Ibn Sahl mostrando seu conhecimento da lei da refração

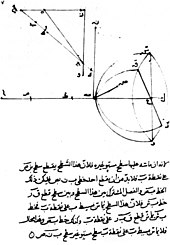
Durante a Idade Média , as idéias gregas sobre óptica foram ressuscitadas e estendidas por escritores do mundo muçulmano . Um dos primeiros foi Al-Kindi (c. 801–873), que escreveu sobre os méritos das ideias aristotélicas e euclidianas da óptica, favorecendo a teoria da emissão, uma vez que poderia quantificar melhor os fenômenos ópticos. Em 984, o matemático persa Ibn Sahl escreveu o tratado "Sobre a queima de espelhos e lentes", descrevendo corretamente uma lei de refração equivalente à lei de Snell. Ele usou essa lei para calcular formas ótimas para lentes e espelhos curvos . No início do século XI, Alhazen (Ibn al-Haytham) escreveu o Livro da Óptica ( Kitab al-manazir ) no qual explorou a reflexão e a refração e propôs um novo sistema para explicar a visão e a luz com base na observação e na experiência. Ele rejeitou a "teoria da emissão" da óptica ptolomaica com seus raios sendo emitidos pelo olho e, em vez disso, apresentou a ideia de que a luz refletia em todas as direções em linhas retas de todos os pontos dos objetos vistos e então entrava no olho, embora ele foi incapaz de explicar corretamente como o olho capturou os raios. O trabalho de Alhazen foi amplamente ignorado no mundo árabe, mas foi traduzido anonimamente para o latim por volta de 1200 dC e posteriormente resumido e expandido pelo monge polonês Witelo , tornando-o um texto padrão sobre óptica na Europa pelos próximos 400 anos.

No século 13 na Europa medieval, o bispo inglês Robert Grosseteste escreveu sobre uma ampla gama de tópicos científicos e discutiu a luz de quatro perspectivas diferentes: uma epistemologia da luz, uma metafísica ou cosmogonia da luz, uma etiologia ou física da luz e uma teologia da luz, baseando-se nas obras de Aristóteles e do Platonismo. O discípulo mais famoso de Grosseteste, Roger Bacon , escreveu obras citando uma ampla gama de obras ópticas e filosóficas recentemente traduzidas, incluindo as de Alhazen, Aristóteles, Avicena , Averróis , Euclides, al-Kindi, Ptolomeu, Tideus e Constantino, o Africano . Bacon foi capaz de usar partes de esferas de vidro como lupas para demonstrar que a luz reflete nos objetos em vez de ser liberada deles.

Os primeiros óculos vestíveis foram inventados na Itália por volta de 1286. Este foi o início da indústria ótica de polimento e polimento de lentes para esses "óculos", primeiro em Veneza e Florença no século XIII, e mais tarde nos centros de fabricação de óculos em ambos os Holanda e Alemanha. Os fabricantes de óculos criaram tipos aprimorados de lentes para a correção da visão com base mais no conhecimento empírico obtido da observação dos efeitos das lentes, em vez de usar a teoria óptica rudimentar da época (teoria que, na maioria das vezes, nem conseguia explicar adequadamente como os óculos funcionavam ). Esse desenvolvimento prático, domínio e experimentação com lentes levaram diretamente à invenção do microscópio óptico composto por volta de 1595 e do telescópio refrator em 1608, ambos os quais apareceram nos centros de fabricação de óculos na Holanda.

O primeiro tratado sobre óptica de Johannes Kepler , Ad Vitellionem paralipomena quibus astronomiae pars optica traditur (1604)

Capa da primeira edição de Newton's Opticks (1704)

Placa com dispositivos ópticos, 1728 Cyclopaedia

No início do século XVII, Johannes Kepler expandiu a óptica geométrica em seus escritos, abrangendo lentes, reflexos de espelhos planos e curvos, os princípios das câmeras pinhole , a lei do quadrado inverso que rege a intensidade da luz e as explicações ópticas de fenômenos astronômicos como como eclipses lunares e solares e paralaxe astronômica . Ele também foi capaz de deduzir corretamente o papel da retina como o órgão real que registra as imagens, finalmente sendo capaz de quantificar cientificamente os efeitos de diferentes tipos de lentes que os fabricantes de óculos observaram nos últimos 300 anos. Após a invenção do telescópio, Kepler estabeleceu a base teórica de como eles funcionavam e descreveu uma versão melhorada, conhecida como telescópio Kepleriano , usando duas lentes convexas para produzir maior ampliação.

A teoria óptica progrediu em meados do século XVII com tratados escritos pelo filósofo René Descartes , que explicavam uma variedade de fenômenos ópticos, incluindo reflexão e refração, assumindo que a luz era emitida por objetos que a produziam. Isso diferia substancialmente da antiga teoria de emissão grega. No final da década de 1660 e início da década de 1670, Isaac Newton expandiu as ideias de Descartes em uma teoria do corpúsculo da luz , determinando que a luz branca era uma mistura de cores que podem ser separadas em suas partes componentes com um prisma . Em 1690, Christiaan Huygens propôs uma teoria ondulatória para a luz baseada nas sugestões feitas por Robert Hooke em 1664. O próprio Hooke criticou publicamente as teorias da luz de Newton e a rixa entre os dois durou até a morte de Hooke. Em 1704, Newton publicou Opticks e, na época, em parte por causa de seu sucesso em outras áreas da física, era geralmente considerado o vencedor no debate sobre a natureza da luz.

A óptica newtoniana foi geralmente aceita até o início do século 19, quando Thomas Young e Augustin-Jean Fresnel conduziram experimentos sobre a interferência da luz que estabeleceu firmemente a natureza ondulatória da luz. O famoso experimento de fenda dupla de Young mostrou que a luz seguia o princípio da superposição , que é uma propriedade semelhante à onda não prevista pela teoria dos corpúsculos de Newton. Este trabalho levou a uma teoria da difração da luz e abriu toda uma área de estudo em óptica física. A óptica de onda foi unificada com sucesso com a teoria eletromagnética por James Clerk Maxwell na década de 1860.

O próximo desenvolvimento na teoria óptica veio em 1899, quando Max Planck modelou corretamente a radiação do corpo negro assumindo que a troca de energia entre a luz e a matéria ocorria apenas em quantidades discretas que ele chamou de quanta . Em 1905, Albert Einstein publicou a teoria do efeito fotoelétrico que estabeleceu firmemente a quantização da própria luz. Em 1913, Niels Bohr mostrou que os átomos só podiam emitir quantidades discretas de energia, explicando assim as linhas discretas vistas nos espectros de emissão e absorção . A compreensão da interação entre luz e matéria que se seguiu a esses desenvolvimentos não apenas formou a base da óptica quântica, mas também foi crucial para o desenvolvimento da mecânica quântica como um todo. A culminação final, a teoria da eletrodinâmica quântica , explica todos os processos ópticos e eletromagnéticos em geral como resultado da troca de fótons reais e virtuais . A óptica quântica ganhou importância prática com as invenções do maser em 1953 e do laser em 1960.

Seguindo o trabalho de Paul Dirac na teoria quântica de campos , George Sudarshan , Roy J. Glauber e Leonard Mandel aplicaram a teoria quântica ao campo eletromagnético nas décadas de 1950 e 1960 para obter uma compreensão mais detalhada da fotodetecção e das estatísticas da luz.

óptica clássica

A óptica clássica é dividida em dois ramos principais: óptica geométrica (ou de raios) e óptica física (ou de onda). Na óptica geométrica, considera-se que a luz viaja em linhas retas, enquanto na óptica física, a luz é considerada como uma onda eletromagnética.

A óptica geométrica pode ser vista como uma aproximação da óptica física que se aplica quando o comprimento de onda da luz usada é muito menor que o tamanho dos elementos ópticos no sistema que está sendo modelado.

óptica geométrica

Geometria de reflexão e refração dos raios de luz

A óptica geométrica , ou óptica de raios , descreve a propagação da luz em termos de "raios" que viajam em linhas retas e cujos caminhos são regidos pelas leis de reflexão e refração nas interfaces entre diferentes meios. Essas leis foram descobertas empiricamente já em 984 dC e têm sido usadas no projeto de componentes e instrumentos ópticos desde então até os dias atuais. Eles podem ser resumidos da seguinte forma:

Quando um raio de luz atinge o limite entre dois materiais transparentes, ele é dividido em um raio refletido e um refratado.

A lei da reflexão diz que o raio refletido está no plano de incidência, e o ângulo de reflexão é igual ao ângulo de incidência.

A lei da refração diz que o raio refratado está no plano de incidência, e o seno do ângulo de incidência dividido pelo seno do ângulo de refração é uma constante:

${\displaystyle {\frac {\sin {\theta _{1}}}{\sin {\theta _{2}}}}=n}$,

onde n é uma constante para quaisquer dois materiais e uma dada cor de luz. Se o primeiro material for ar ou vácuo, n é o índice de refração do segundo material.

As leis de reflexão e refração podem ser derivadas do princípio de Fermat , que afirma que o caminho percorrido entre dois pontos por um raio de luz é o caminho que pode ser percorrido no menor tempo.

aproximações

A óptica geométrica é muitas vezes simplificada fazendo a aproximação paraxial , ou "aproximação de pequeno ângulo". O comportamento matemático torna-se então linear, permitindo que componentes e sistemas ópticos sejam descritos por matrizes simples. Isso leva às técnicas de óptica gaussiana e rastreamento de raios paraxiais , que são usadas para encontrar propriedades básicas de sistemas ópticos, como imagens aproximadas e posições e ampliações de objetos .

Reflexões

Diagrama de reflexão especular

As reflexões podem ser divididas em dois tipos: reflexão especular e reflexão difusa . A reflexão especular descreve o brilho de superfícies como espelhos, que refletem a luz de maneira simples e previsível. Isso permite a produção de imagens refletidas que podem ser associadas a uma localização real ( real ) ou extrapolada ( virtual ) no espaço. A reflexão difusa descreve materiais não brilhantes, como papel ou pedra. As reflexões dessas superfícies só podem ser descritas estatisticamente, com a distribuição exata da luz refletida dependendo da estrutura microscópica do material. Muitos refletores difusos são descritos ou podem ser aproximados pela lei dos cossenos de Lambert , que descreve superfícies que têm luminância igual quando vistas de qualquer ângulo. Superfícies brilhantes podem dar reflexão especular e difusa.

Na reflexão especular, a direção do raio refletido é determinada pelo ângulo que o raio incidente faz com a superfície normal , uma linha perpendicular à superfície no ponto onde o raio atinge. Os raios incidente e refletido e a normal estão em um único plano, e o ângulo entre o raio refletido e a superfície normal é o mesmo que entre o raio incidente e a normal. Isso é conhecido como a Lei da Reflexão .

Para espelhos planos , a lei da reflexão implica que as imagens dos objetos estão na vertical e à mesma distância atrás do espelho que os objetos estão na frente do espelho. O tamanho da imagem é igual ao tamanho do objeto. A lei também implica que as imagens espelhadas são invertidas em paridade, o que percebemos como uma inversão esquerda-direita. As imagens formadas pela reflexão em dois (ou qualquer número par de) espelhos não são invertidas em paridade. Os refletores de canto produzem raios refletidos que viajam de volta na direção de onde vieram os raios incidentes. Isso é chamado de retrorreflexão .

Espelhos com superfícies curvas podem ser modelados por traçado de raios e usando a lei de reflexão em cada ponto da superfície. Para espelhos com superfícies parabólicas , raios paralelos incidentes no espelho produzem raios refletidos que convergem em um foco comum . Outras superfícies curvas também podem focalizar a luz, mas com aberrações devido à forma divergente fazendo com que o foco seja espalhado no espaço. Em particular, espelhos esféricos exibem aberrações esféricas . Espelhos curvos podem formar imagens com ampliação maior ou menor que um, e a ampliação pode ser negativa, indicando que a imagem está invertida. Uma imagem vertical formada pela reflexão em um espelho é sempre virtual, enquanto uma imagem invertida é real e pode ser projetada em uma tela.

refrações

Ilustração da Lei de Snell para o caso n ₁ < n ₂ , como interface ar/água

A refração ocorre quando a luz viaja através de uma área do espaço que tem um índice de refração variável; este princípio permite lentes e o foco da luz. O caso mais simples de refração ocorre quando existe uma interface entre um meio uniforme com índice de refração e outro meio com índice de refração . Em tais situações, a Lei de Snell descreve a deflexão resultante do raio de luz: ${\displaystyle n_{1}}$${\displaystyle n_{2}}$

${\displaystyle n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}\ }$

onde e são os ângulos entre a normal (à interface) e as ondas incidente e refratada, respectivamente. ${\displaystyle \theta _{1}}$${\displaystyle \theta _{2}}$

O índice de refração de um meio está relacionado com a velocidade, v , da luz nesse meio por

${\displaystyle n=c/v}$,

onde c é a velocidade da luz no vácuo .

A Lei de Snell pode ser usada para prever a deflexão dos raios de luz quando eles passam por um meio linear, desde que os índices de refração e a geometria do meio sejam conhecidos. Por exemplo, a propagação da luz através de um prisma resulta no desvio do raio de luz dependendo da forma e orientação do prisma. Na maioria dos materiais, o índice de refração varia com a frequência da luz. Levando isso em consideração, a Lei de Snell pode ser usada para prever como um prisma irá dispersar a luz em um espectro. A descoberta desse fenômeno ao passar a luz através de um prisma é notoriamente atribuída a Isaac Newton.

Alguns meios têm um índice de refração que varia gradualmente com a posição e, portanto, os raios de luz no meio são curvos. Esse efeito é responsável pelas miragens observadas em dias quentes: uma mudança no índice de refração do ar com a altura faz com que os raios de luz se dobrem, criando a aparência de reflexos especulares ao longe (como se estivessem na superfície de uma poça d'água). Materiais ópticos com índices variados de refração são chamados de materiais de índice de gradiente (GRIN). Esses materiais são usados ​​para fazer óptica de índice de gradiente .

Para raios de luz que viajam de um material com alto índice de refração para um material com baixo índice de refração, a lei de Snell prevê que não há quando é grande. Nesse caso, não ocorre transmissão; toda a luz é refletida. Esse fenômeno é chamado de reflexão interna total e permite a tecnologia de fibra óptica. À medida que a luz viaja por uma fibra óptica, ela sofre reflexão interna total, permitindo que praticamente nenhuma luz seja perdida ao longo do comprimento do cabo. ${\displaystyle \theta _{2}}$${\displaystyle \theta _{1}}$

Lentes

Um diagrama de rastreamento de raios para uma lente convergente

Um dispositivo que produz raios de luz convergentes ou divergentes devido à refração é conhecido como lente . As lentes são caracterizadas por sua distância focal : uma lente convergente tem distância focal positiva, enquanto uma lente divergente tem distância focal negativa. A distância focal menor indica que a lente tem um efeito convergente ou divergente mais forte. A distância focal de uma lente simples no ar é dada pela equação do fabricante da lente .

O rastreamento de raios pode ser usado para mostrar como as imagens são formadas por uma lente. Para uma lente fina no ar, a localização da imagem é dada pela equação simples

${\displaystyle {\frac {1}{S_{1}}}+{\frac {1}{S_{2}}}={\frac {1}{f}}}$,

onde é a distância do objeto à lente, é a distância da lente à imagem e é a distância focal da lente. Na convenção de sinais usada aqui, as distâncias do objeto e da imagem são positivas se o objeto e a imagem estiverem em lados opostos da lente. ${\displaystyle S_{1}}$${\displaystyle S_{2}}$${\displaystyle f}$

Os raios paralelos que chegam são focados por uma lente convergente em um ponto a uma distância focal da lente, no lado oposto da lente. Isso é chamado de ponto focal traseiro da lente. Os raios de um objeto a uma distância finita são focados mais longe da lente do que a distância focal; quanto mais próximo o objeto estiver da lente, mais longe a imagem estará da lente.

Com lentes divergentes, os raios paralelos incidentes divergem após passarem pela lente, de tal forma que parecem ter se originado em um ponto a uma distância focal à frente da lente. Este é o ponto focal frontal da lente. Os raios de um objeto a uma distância finita estão associados a uma imagem virtual que está mais próxima da lente do que do ponto focal e do mesmo lado da lente que o objeto. Quanto mais próximo o objeto estiver da lente, mais próxima a imagem virtual estará da lente. Assim como nos espelhos, as imagens verticais produzidas por uma única lente são virtuais, enquanto as imagens invertidas são reais.

As lentes sofrem de aberrações que distorcem as imagens. As aberrações monocromáticas ocorrem porque a geometria da lente não direciona perfeitamente os raios de cada ponto do objeto para um único ponto na imagem, enquanto a aberração cromática ocorre porque o índice de refração da lente varia com o comprimento de onda da luz.

Imagens de letras pretas em uma lente convexa fina de distância focal f   são mostradas em vermelho. Os raios selecionados são mostrados para as letras E , I e K em azul, verde e laranja, respectivamente. Note que E (em 2 f ) tem uma imagem de igual tamanho, real e invertida; I (em f ) tem sua imagem no infinito; e K (em f /2) tem uma imagem de tamanho duplo, virtual e vertical.

Óptica física

Na ótica física, considera-se que a luz se propaga como uma onda. Este modelo prevê fenômenos como interferência e difração, que não são explicados pela óptica geométrica. A velocidade das ondas de luz no ar é de aproximadamente 3,0 × 10 ⁸  m/s (exatamente 299.792.458 m/s no vácuo ). O comprimento de onda das ondas de luz visível varia entre 400 e 700 nm, mas o termo "luz" também é frequentemente aplicado ao infravermelho (0,7 a 300 μm) e à radiação ultravioleta (10 a 400 nm).

O modelo de onda pode ser usado para fazer previsões sobre como um sistema óptico se comportará sem exigir uma explicação do que está "ondulando" em qual meio. Até meados do século 19, a maioria dos físicos acreditava em um meio "etéreo" no qual a perturbação da luz se propagava. A existência de ondas eletromagnéticas foi prevista em 1865 pelas equações de Maxwell . Essas ondas se propagam na velocidade da luz e possuem campos elétricos e magnéticos variáveis ​​que são ortogonais entre si e também à direção de propagação das ondas. As ondas de luz agora são geralmente tratadas como ondas eletromagnéticas, exceto quando os efeitos da mecânica quântica devem ser considerados.

Modelagem e projeto de sistemas ópticos usando óptica física

Muitas aproximações simplificadas estão disponíveis para analisar e projetar sistemas ópticos. A maioria deles usa uma única quantidade escalar para representar o campo elétrico da onda de luz, em vez de usar um modelo vetorial com vetores elétricos e magnéticos ortogonais. A equação de Huygens-Fresnel é um desses modelos. Isso foi derivado empiricamente por Fresnel em 1815, com base na hipótese de Huygens de que cada ponto em uma frente de onda gera uma frente de onda esférica secundária, que Fresnel combinou com o princípio da superposição de ondas . A equação de difração de Kirchhoff , que é derivada usando as equações de Maxwell, coloca a equação de Huygens-Fresnel em uma base física mais firme. Exemplos da aplicação do princípio de Huygens-Fresnel podem ser encontrados nos artigos sobre difração e difração de Fraunhofer .

Modelos mais rigorosos, envolvendo a modelagem de campos elétricos e magnéticos da onda de luz, são necessários quando se trata de materiais cujas propriedades elétricas e magnéticas afetam a interação da luz com o material. Por exemplo, o comportamento de uma onda de luz interagindo com uma superfície metálica é bem diferente do que ocorre quando ela interage com um material dielétrico. Um modelo vetorial também deve ser usado para modelar a luz polarizada.

Técnicas de modelagem numérica , como o método dos elementos finitos , o método dos elementos de contorno e o método da matriz da linha de transmissão, podem ser usados ​​para modelar a propagação da luz em sistemas que não podem ser resolvidos analiticamente. Tais modelos são computacionalmente exigentes e normalmente são usados ​​apenas para resolver problemas de pequena escala que exigem precisão além daquela que pode ser alcançada com soluções analíticas.

Todos os resultados da óptica geométrica podem ser recuperados usando as técnicas da óptica de Fourier , que aplicam muitas das mesmas técnicas matemáticas e analíticas usadas na engenharia acústica e no processamento de sinais .

A propagação de feixe gaussiano é um modelo de óptica física paraxial simples para a propagação de radiação coerente, como feixes de laser. Essa técnica considera parcialmente a difração, permitindo cálculos precisos da taxa na qual um feixe de laser se expande com a distância e o tamanho mínimo para o qual o feixe pode ser focalizado. A propagação do feixe gaussiano preenche a lacuna entre a óptica geométrica e a óptica física.

Superposição e interferência

Na ausência de efeitos não lineares , o princípio da superposição pode ser usado para prever a forma de formas de onda interativas através da simples adição de perturbações. Essa interação de ondas para produzir um padrão resultante é geralmente chamada de "interferência" e pode resultar em uma variedade de resultados. Se duas ondas de mesmo comprimento de onda e frequência estiverem em fase , ambas as cristas e vales das ondas se alinham. Isso resulta em interferência construtiva e aumento da amplitude da onda, que para a luz está associada a um brilho da forma de onda naquele local. Alternativamente, se as duas ondas do mesmo comprimento de onda e frequência estiverem fora de fase, as cristas das ondas se alinharão com os vales das ondas e vice-versa. Isso resulta em interferência destrutiva e diminuição da amplitude da onda, que para a luz está associada a um escurecimento da forma de onda naquele local. Veja abaixo uma ilustração desse efeito.

forma de onda combinada
onda 1
onda 2
	Duas ondas em fase	Duas ondas 180° fora de fase

Quando óleo ou combustível é derramado, padrões coloridos são formados por interferência de película fina.

Como o princípio de Huygens-Fresnel afirma que cada ponto de uma frente de onda está associado à produção de uma nova perturbação, é possível que uma frente de onda interfira consigo mesma de forma construtiva ou destrutiva em diferentes locais, produzindo franjas claras e escuras em padrões regulares e previsíveis. A interferometria é a ciência de medir esses padrões, geralmente como um meio de fazer determinações precisas de distâncias ou resoluções angulares . O interferômetro de Michelson era um instrumento famoso que usava efeitos de interferência para medir com precisão a velocidade da luz.

A aparência de filmes finos e revestimentos é diretamente afetada por efeitos de interferência. Os revestimentos antirreflexo usam interferência destrutiva para reduzir a refletividade das superfícies que revestem e podem ser usados ​​para minimizar o brilho e reflexos indesejados. O caso mais simples é uma única camada com espessura de um quarto do comprimento de onda da luz incidente. A onda refletida do topo do filme e a onda refletida da interface filme/material ficam exatamente 180° fora de fase, causando interferência destrutiva. As ondas estão exatamente fora de fase para um comprimento de onda, que normalmente seria escolhido para estar próximo ao centro do espectro visível, em torno de 550 nm. Projetos mais complexos usando várias camadas podem atingir baixa refletividade em uma banda larga ou refletividade extremamente baixa em um único comprimento de onda.

A interferência construtiva em filmes finos pode criar um forte reflexo de luz em uma faixa de comprimentos de onda, que pode ser estreito ou amplo, dependendo do design do revestimento. Esses filmes são usados ​​para fazer espelhos dielétricos , filtros de interferência , refletores de calor e filtros para separação de cores em câmeras de televisão em cores . Esse efeito de interferência também é o que causa os padrões coloridos do arco-íris vistos nas manchas de óleo.

Difração e resolução óptica

Difração em duas fendas separadas pela distância . As franjas brilhantes ocorrem ao longo de linhas onde linhas pretas se cruzam com linhas pretas e linhas brancas se cruzam com linhas brancas. Essas franjas são separadas por ângulo e são numeradas de acordo com a ordem .${\displaystyle d}$${\displaystyle \theta}$${\displaystyle n}$

A difração é o processo pelo qual a interferência da luz é mais comumente observada. O efeito foi descrito pela primeira vez em 1665 por Francesco Maria Grimaldi , que também cunhou o termo do latim diffringere , 'quebrar em pedaços'. Mais tarde naquele século, Robert Hooke e Isaac Newton também descreveram fenômenos agora conhecidos como difração nos anéis de Newton , enquanto James Gregory registrou suas observações de padrões de difração de penas de pássaros.

O primeiro modelo de óptica física de difração que se baseava no princípio de Huygens-Fresnel foi desenvolvido em 1803 por Thomas Young em seus experimentos de interferência com os padrões de interferência de duas fendas próximas umas das outras. Young mostrou que seus resultados só poderiam ser explicados se as duas fendas agissem como duas fontes únicas de ondas em vez de corpúsculos. Em 1815 e 1818, Augustin-Jean Fresnel estabeleceu firmemente a matemática de como a interferência de ondas pode explicar a difração.

Os modelos físicos mais simples de difração usam equações que descrevem a separação angular das franjas claras e escuras devido à luz de um determinado comprimento de onda (λ). Em geral, a equação assume a forma

${\displaystyle m\lambda =d\sin \theta }$

onde é a separação entre duas fontes de frente de onda (no caso dos experimentos de Young, eram duas fendas ), é a separação angular entre a franja central e a franja de enésima ordem, onde o máximo central é . ${\displaystyle d}$${\displaystyle \theta}$${\displaystyle m}$${\displaystyle m=0}$

Esta equação é ligeiramente modificada para levar em conta uma variedade de situações, como difração através de um único intervalo, difração através de fendas múltiplas ou difração através de uma grade de difração que contém um grande número de fendas com espaçamento igual. Modelos de difração mais complicados requerem trabalhar com a matemática da difração de Fresnel ou Fraunhofer.

A difração de raios-X faz uso do fato de que os átomos em um cristal têm espaçamento regular em distâncias que são da ordem de um angstrom . Para ver os padrões de difração, raios-x com comprimentos de onda semelhantes a esse espaçamento são passados ​​através do cristal. Como os cristais são objetos tridimensionais em vez de grades bidimensionais, o padrão de difração associado varia em duas direções de acordo com a reflexão de Bragg , com os pontos brilhantes associados ocorrendo em padrões únicos e sendo o dobro do espaçamento entre os átomos. ${\displaystyle d}$

Os efeitos de difração limitam a capacidade de um detector óptico de resolver opticamente fontes de luz separadas. Em geral, a luz que passa por uma abertura sofrerá difração e as melhores imagens que podem ser criadas (conforme descrito em óptica limitada por difração ) aparecem como um ponto central com anéis brilhantes circundantes, separados por nulos escuros; este padrão é conhecido como padrão de Airy , e o lóbulo brilhante central como um disco de Airy . O tamanho desse disco é dado por

${\displaystyle \sin \theta =1.22{\frac {\lambda }{D}}}$

onde θ é a resolução angular, λ é o comprimento de onda da luz e D é o diâmetro da abertura da lente. Se a separação angular dos dois pontos for significativamente menor que o raio angular do disco de Airy, então os dois pontos não podem ser resolvidos na imagem, mas se a separação angular for muito maior do que isso, imagens distintas dos dois pontos são formadas e eles pode, portanto, ser resolvido. Rayleigh definiu o " critério de Rayleigh " um tanto arbitrário de que dois pontos cuja separação angular é igual ao raio do disco de Airy (medido até o primeiro nulo, ou seja, até o primeiro lugar onde nenhuma luz é vista) podem ser considerados resolvidos . Pode-se observar que quanto maior o diâmetro da lente ou sua abertura, mais fina é a resolução. A interferometria , com sua capacidade de imitar aberturas de linha de base extremamente grandes, permite a maior resolução angular possível.

Para imagens astronômicas, a atmosfera impede que a resolução ideal seja alcançada no espectro visível devido à dispersão e espalhamento atmosférico que faz com que as estrelas brilhem . Os astrônomos se referem a esse efeito como a qualidade da visão astronômica . Técnicas conhecidas como óptica adaptativa têm sido usadas para eliminar a perturbação atmosférica das imagens e obter resultados que se aproximam do limite de difração.

Dispersão e espalhamento

Animação conceitual de dispersão de luz através de um prisma. A luz de alta frequência (azul) é mais desviada e a de baixa frequência (vermelha) menos.

Os processos refrativos ocorrem no limite da ótica física, onde o comprimento de onda da luz é semelhante a outras distâncias, como uma espécie de espalhamento. O tipo mais simples de espalhamento é o espalhamento de Thomson , que ocorre quando as ondas eletromagnéticas são desviadas por partículas individuais. No limite do espalhamento de Thomson, no qual a natureza ondulatória da luz é evidente, a luz é dispersa independentemente da frequência, em contraste com o espalhamento de Compton , que é dependente da frequência e estritamente um processo mecânico quântico , envolvendo a natureza da luz como partículas. Em um sentido estatístico, a dispersão elástica da luz por numerosas partículas muito menores que o comprimento de onda da luz é um processo conhecido como dispersão de Rayleigh , enquanto o processo semelhante de dispersão por partículas que são semelhantes ou maiores em comprimento de onda é conhecido como dispersão de Mie com o Tyndall sendo um resultado comumente observado. Uma pequena proporção de dispersão de luz de átomos ou moléculas pode sofrer dispersão Raman , em que a frequência muda devido à excitação dos átomos e moléculas. O espalhamento Brillouin ocorre quando a frequência da luz muda devido a mudanças locais com o tempo e movimentos de um material denso.

A dispersão ocorre quando diferentes frequências de luz têm diferentes velocidades de fase , devido às propriedades do material ( dispersão do material ) ou à geometria de um guia de onda óptico ( dispersão do guia de onda ). A forma mais familiar de dispersão é uma diminuição no índice de refração com o aumento do comprimento de onda, que é visto na maioria dos materiais transparentes. Isso é chamado de "dispersão normal". Ocorre em todos os materiais dielétricos , em faixas de comprimento de onda onde o material não absorve luz. Nas faixas de comprimento de onda em que um meio tem absorção significativa, o índice de refração pode aumentar com o comprimento de onda. Isso é chamado de "dispersão anômala".

A separação de cores por um prisma é um exemplo de dispersão normal. Nas superfícies do prisma, a lei de Snell prevê que a luz incidente em um ângulo θ com a normal será refratada em um ângulo arcsin(sin (θ) / n ). Assim, a luz azul, com seu índice de refração mais alto, é curvada mais fortemente do que a luz vermelha, resultando no conhecido padrão de arco-íris .

Dispersão: duas senoides se propagando em velocidades diferentes formam um padrão de interferência em movimento. O ponto vermelho se move com a velocidade de fase e os pontos verdes se propagam com a velocidade de grupo . Neste caso, a velocidade de fase é o dobro da velocidade de grupo. O ponto vermelho ultrapassa dois pontos verdes, ao passar da esquerda para a direita da figura. Com efeito, as ondas individuais (que viajam com a velocidade de fase) escapam do pacote de ondas (que viaja com a velocidade de grupo).

A dispersão do material é frequentemente caracterizada pelo número de Abbe , que fornece uma medida simples de dispersão com base no índice de refração em três comprimentos de onda específicos. A dispersão do guia de onda depende da constante de propagação . Ambos os tipos de dispersão causam mudanças nas características do grupo da onda, as características do pacote de ondas que mudam com a mesma frequência que a amplitude da onda eletromagnética. A "dispersão de velocidade de grupo" se manifesta como uma dispersão do "envelope" de sinal da radiação e pode ser quantificada com um parâmetro de atraso de dispersão de grupo:

${\displaystyle D={\frac {1}{v_{g}^{2}}}{\frac {dv_{g}}{d\lambda }}}$

onde é a velocidade de grupo. Para um meio uniforme, a velocidade de grupo é ${\displaystyle v_{g}}$

${\displaystyle v_{g}=c\left(n-\lambda {\frac {dn}{d\lambda }}\right)^{-1}}$

onde n é o índice de refração e c é a velocidade da luz no vácuo. Isso fornece uma forma mais simples para o parâmetro de atraso de dispersão:

${\displaystyle D=-{\frac {\lambda }{c}}\,{\frac {d^{2}n}{d\lambda ^{2}}}.}$

Se D for menor que zero, diz-se que o meio tem dispersão positiva ou dispersão normal. Se D for maior que zero, o meio tem dispersão negativa . Se um pulso de luz é propagado através de um meio normalmente dispersivo, o resultado é que os componentes de frequência mais alta desaceleram mais do que os componentes de frequência mais baixa. O pulso, portanto, torna-se positivamente chirped , ou up-chirped , aumentando em frequência com o tempo. Isso faz com que o espectro que sai de um prisma apareça com a luz vermelha a menos refratada e a luz azul/violeta a mais refratada. Por outro lado, se um pulso viaja através de um meio dispersivo anômalo (negativamente), os componentes de alta frequência viajam mais rápido do que os mais baixos, e o pulso torna-se um chilreado negativo , ou um chilreado baixo , diminuindo a frequência com o tempo.

O resultado da dispersão da velocidade do grupo, seja negativa ou positiva, é, em última instância, a dispersão temporal do pulso. Isso torna o gerenciamento de dispersão extremamente importante em sistemas de comunicações ópticas baseados em fibras ópticas , pois se a dispersão for muito alta, um grupo de pulsos representando informações se espalhará no tempo e se fundirá, impossibilitando a extração do sinal.

Polarização

A polarização é uma propriedade geral das ondas que descreve a orientação de suas oscilações. Para ondas transversais , como muitas ondas eletromagnéticas, descreve a orientação das oscilações no plano perpendicular à direção de propagação da onda. As oscilações podem ser orientadas em uma única direção ( polarização linear ), ou a direção da oscilação pode girar à medida que a onda viaja ( polarização circular ou elíptica ). Ondas circularmente polarizadas podem girar para a direita ou para a esquerda na direção do deslocamento, e qual dessas duas rotações está presente em uma onda é chamada de quiralidade da onda .

A maneira típica de considerar a polarização é acompanhar a orientação do vetor do campo elétrico à medida que a onda eletromagnética se propaga. O vetor campo elétrico de uma onda plana pode ser arbitrariamente dividido em dois componentes perpendiculares denominados x e y (com z indicando a direção do deslocamento). A forma traçada no plano xy pelo vetor campo elétrico é uma figura de Lissajous que descreve o estado de polarização . As figuras a seguir mostram alguns exemplos da evolução do vetor campo elétrico (azul), com o tempo (os eixos verticais), em um determinado ponto do espaço, juntamente com seus componentes x e y (vermelho/esquerda e verde / direita ) , e o caminho traçado pelo vetor no plano (roxo): A mesma evolução ocorreria ao olhar para o campo elétrico em um determinado momento enquanto evoluísse o ponto no espaço, no sentido oposto à propagação.

Linear

Circular

Polarização elíptica

Na figura mais à esquerda acima, os componentes x e y da onda de luz estão em fase. Nesse caso, a proporção de suas forças é constante, de modo que a direção do vetor elétrico (a soma vetorial desses dois componentes) é constante. Como a ponta do vetor traça uma única linha no plano, esse caso especial é chamado de polarização linear. A direção desta linha depende das amplitudes relativas dos dois componentes.

Na figura do meio, os dois componentes ortogonais têm as mesmas amplitudes e estão 90° fora de fase. Neste caso, uma componente é zero quando a outra componente está na amplitude máxima ou mínima. Existem duas relações de fase possíveis que satisfazem este requisito: a componente x pode estar 90° à frente da componente y ou pode estar 90° atrás da componente y . Nesse caso especial, o vetor elétrico traça um círculo no plano, então essa polarização é chamada de polarização circular. A direção de rotação no círculo depende de qual das relações bifásicas existe e corresponde à polarização circular à direita e à polarização circular à esquerda .

Em todos os outros casos, onde os dois componentes não têm as mesmas amplitudes e/ou sua diferença de fase não é zero nem múltiplo de 90°, a polarização é chamada de polarização elíptica porque o vetor elétrico traça uma elipse no plano ( a elipse de polarização ). Isso é mostrado na figura acima à direita. A matemática detalhada da polarização é feita usando o cálculo de Jones e é caracterizada pelos parâmetros de Stokes .

Mudando a polarização

Meios que possuem diferentes índices de refração para diferentes modos de polarização são chamados de birrefringentes . Manifestações bem conhecidas deste efeito aparecem em placas /retardadores de ondas ópticas (modos lineares) e na rotação de Faraday / rotação óptica (modos circulares). Se o comprimento do caminho no meio birrefringente for suficiente, as ondas planas sairão do material com uma direção de propagação significativamente diferente, devido à refração. Por exemplo, este é o caso dos cristais macroscópicos de calcita , que apresentam ao observador duas imagens deslocadas e ortogonalmente polarizadas de tudo o que é visto através deles. Foi esse efeito que forneceu a primeira descoberta da polarização, por Erasmus Bartholinus em 1669. Além disso, a mudança de fase e, portanto, a mudança no estado de polarização geralmente depende da frequência, o que, em combinação com o dicroísmo , geralmente dá origem a brilhos cores e efeitos de arco-íris. Na mineralogia , essas propriedades, conhecidas como pleocroísmo , são frequentemente exploradas com o objetivo de identificar minerais usando microscópios de polarização. Além disso, muitos plásticos que normalmente não são birrefringentes se tornarão quando sujeitos a estresse mecânico , um fenômeno que é a base da fotoelasticidade . Métodos não birrefringentes, para girar a polarização linear de feixes de luz, incluem o uso de rotadores de polarização prismática que usam reflexão interna total em um conjunto de prismas projetado para transmissão colinear eficiente.

Um polarizador que altera a orientação da luz linearmente polarizada.
Nesta figura, θ ₁ – θ ₀ = θ _i .

Os meios que reduzem a amplitude de certos modos de polarização são chamados dicróicos , com dispositivos que bloqueiam quase toda a radiação em um modo conhecidos como filtros polarizadores ou simplesmente " polarizadores ". A lei de Malus, que leva o nome de Étienne-Louis Malus , diz que quando um polarizador perfeito é colocado em um feixe de luz polarizado linear, a intensidade, I , da luz que passa é dada por

${\displaystyle I=I_{0}\cos ^{2}\theta _{i}\quad ,}$

onde

I ₀ é a intensidade inicial,

e θ _i é o ângulo entre a direção de polarização inicial da luz e o eixo do polarizador.

Um feixe de luz não polarizada pode ser pensado como contendo uma mistura uniforme de polarizações lineares em todos os ângulos possíveis. Como o valor médio de é 1/2, o coeficiente de transmissão torna-se ${\displaystyle \cos ^{2}\theta }$

${\displaystyle {\frac {I}{I_{0}}}={\frac {1}{2}}\quad }$

Na prática, alguma luz é perdida no polarizador e a transmissão real de luz não polarizada será um pouco menor do que isso, cerca de 38% para polarizadores do tipo Polaroid, mas consideravelmente maior (>49,9%) para alguns tipos de prisma birrefringente.

Além da birrefringência e dicroísmo em meios estendidos, efeitos de polarização também podem ocorrer na interface (refletiva) entre dois materiais de diferentes índices de refração. Esses efeitos são tratados pelas equações de Fresnel . Parte da onda é transmitida e parte é refletida, com a proporção dependendo do ângulo de incidência e do ângulo de refração. Desta forma, a ótica física recupera o ângulo de Brewster . Quando a luz reflete de um filme fino em uma superfície, a interferência entre os reflexos das superfícies do filme pode produzir polarização na luz refletida e transmitida.

Luz natural

Os efeitos de um filtro polarizador no céu em uma fotografia. A foto da esquerda foi tirada sem polarizador. Para a imagem certa, o filtro foi ajustado para eliminar certas polarizações da luz azul espalhada do céu.

A maioria das fontes de radiação eletromagnética contém um grande número de átomos ou moléculas que emitem luz. A orientação dos campos elétricos produzidos por esses emissores pode não estar correlacionada , caso em que a luz é dita não polarizada . Se houver correlação parcial entre os emissores, a luz é parcialmente polarizada . Se a polarização for consistente em todo o espectro da fonte, a luz parcialmente polarizada pode ser descrita como uma superposição de um componente completamente não polarizado e um completamente polarizado. Pode-se então descrever a luz em termos do grau de polarização e os parâmetros da elipse de polarização.

A luz refletida por materiais transparentes brilhantes é parcial ou totalmente polarizada, exceto quando a luz é normal (perpendicular) à superfície. Foi esse efeito que permitiu ao matemático Étienne-Louis Malus fazer as medições que permitiram o desenvolvimento dos primeiros modelos matemáticos para a luz polarizada. A polarização ocorre quando a luz é espalhada na atmosfera . A luz espalhada produz o brilho e a cor em céu claro . Esta polarização parcial da luz espalhada pode ser aproveitada usando filtros polarizadores para escurecer o céu nas fotografias . A polarização óptica é principalmente de importância em química devido ao dicroísmo circular e rotação óptica (" birrefringência circular ") exibida por moléculas opticamente ativas ( quirais ) .

óptica moderna

A óptica moderna abrange as áreas da ciência e engenharia óptica que se tornaram populares no século XX. Essas áreas da ciência óptica normalmente se relacionam com as propriedades eletromagnéticas ou quânticas da luz, mas incluem outros tópicos. Um importante subcampo da ótica moderna, a ótica quântica , trata especificamente das propriedades mecânicas quânticas da luz. A óptica quântica não é apenas teórica; alguns dispositivos modernos, como lasers, têm princípios de operação que dependem da mecânica quântica. Detectores de luz, como fotomultiplicadores e channeltrons , respondem a fótons individuais. Sensores eletrônicos de imagem , como CCDs , exibem ruído de tiro correspondente às estatísticas de eventos de fótons individuais. Diodos emissores de luz e células fotovoltaicas também não podem ser compreendidos sem a mecânica quântica. No estudo desses dispositivos, a óptica quântica frequentemente se sobrepõe à eletrônica quântica .

As áreas de especialidade da pesquisa em óptica incluem o estudo de como a luz interage com materiais específicos, como na óptica de cristal e metamateriais . Outras pesquisas se concentram na fenomenologia das ondas eletromagnéticas como em óptica singular , óptica sem imagem , óptica não linear , óptica estatística e radiometria . Além disso, os engenheiros de computação se interessaram por óptica integrada , visão de máquina e computação fotônica como possíveis componentes da "próxima geração" de computadores.

Hoje, a ciência pura da óptica é chamada de ciência óptica ou física óptica para distingui-la das ciências ópticas aplicadas, que são chamadas de engenharia óptica . Subcampos proeminentes da engenharia óptica incluem engenharia de iluminação , fotônica e optoeletrônica com aplicações práticas como design de lentes , fabricação e teste de componentes ópticos e processamento de imagem . Alguns desses campos se sobrepõem, com fronteiras nebulosas entre os termos dos assuntos que significam coisas ligeiramente diferentes em diferentes partes do mundo e em diferentes áreas da indústria. Uma comunidade profissional de pesquisadores em óptica não linear se desenvolveu nas últimas décadas devido aos avanços na tecnologia laser.

lasers

Experimentos como este com lasers de alta potência fazem parte da pesquisa ótica moderna.

Um laser é um dispositivo que emite luz, uma espécie de radiação eletromagnética, por meio de um processo denominado emissão estimulada . O termo laser é um acrônimo para Light Amplification by Stimulated Emission of Radiation . A luz do laser geralmente é espacialmente coerente , o que significa que a luz é emitida em um feixe estreito e de baixa divergência ou pode ser convertida em um com a ajuda de componentes ópticos, como lentes. Como o equivalente em micro-ondas do laser, o maser , foi desenvolvido primeiro, os dispositivos que emitem micro-ondas e frequências de rádio são geralmente chamados de masers .

Estrela guia laser do VLT

O primeiro laser funcional foi demonstrado em 16 de maio de 1960 por Theodore Maiman no Hughes Research Laboratories . Quando inventados, eles foram chamados de "uma solução procurando um problema". Desde então, os lasers se tornaram uma indústria multibilionária, encontrando utilidade em milhares de aplicações altamente variadas. A primeira aplicação de laser visível na vida diária da população em geral foi o scanner de código de barras de supermercado , lançado em 1974. O reprodutor de laserdisc , lançado em 1978, foi o primeiro produto de consumo de sucesso a incluir um laser, mas o reprodutor de CD foi o primeiro dispositivo equipado com laser a se tornar realmente comum nas casas dos consumidores, a partir de 1982. Esses dispositivos de armazenamento óptico usam um laser semicondutor com menos de um milímetro de largura para escanear a superfície do disco para recuperação de dados. A comunicação por fibra óptica depende de lasers para transmitir grandes quantidades de informações na velocidade da luz. Outras aplicações comuns de lasers incluem impressoras a laser e ponteiros a laser . Os lasers são usados ​​na medicina em áreas como cirurgia sem sangue , cirurgia ocular a laser e microdissecção por captura a laser e em aplicações militares , como sistemas de defesa antimísseis , contramedidas eletro-ópticas (EOCM) e lidar . Lasers também são usados ​​em hologramas , bubblegrams , shows de luz laser e depilação a laser .

Efeito Kapitsa-Dirac

O efeito Kapitsa-Dirac faz com que os feixes de partículas sejam difratados como resultado do encontro de uma onda estacionária de luz. A luz pode ser usada para posicionar a matéria usando vários fenômenos (ver pinças ópticas ).

Formulários

A ótica faz parte da vida cotidiana. A onipresença dos sistemas visuais na biologia indica o papel central que a óptica desempenha como a ciência de um dos cinco sentidos . Muitas pessoas se beneficiam de óculos ou lentes de contato , e a ótica é essencial para o funcionamento de muitos bens de consumo, incluindo câmeras . Arco-íris e miragens são exemplos de fenômenos ópticos. A comunicação óptica fornece o backbone tanto para a Internet quanto para a telefonia moderna .

Olho humano

Modelo de um olho humano. As características mencionadas neste artigo são 1. humor vítreo 3. músculo ciliar , 6. pupila , 7. câmara anterior , 8. córnea , 10. córtex do cristalino , 22. nervo óptico , 26. fóvea , 30. retina .

O olho humano funciona focalizando a luz em uma camada de células fotorreceptoras chamada retina, que forma o revestimento interno da parte posterior do olho. A focalização é realizada por uma série de meios transparentes. A luz que entra no olho passa primeiro pela córnea, que fornece grande parte da potência óptica do olho. A luz então continua através do fluido logo atrás da córnea - a câmara anterior , passando então pela pupila . A luz então passa pela lente , que focaliza ainda mais a luz e permite o ajuste do foco. A luz então passa pelo corpo principal do fluido no olho - o humor vítreo , e atinge a retina. As células da retina revestem a parte de trás do olho, exceto onde sai o nervo óptico; isso resulta em um ponto cego .

Existem dois tipos de células fotorreceptoras, bastonetes e cones, que são sensíveis a diferentes aspectos da luz. Os bastonetes são sensíveis à intensidade da luz em uma ampla faixa de frequência, portanto, são responsáveis ​​pela visão em preto e branco . Os bastonetes não estão presentes na fóvea, a área da retina responsável pela visão central, e não respondem tanto quanto os cones às mudanças espaciais e temporais da luz. Há, no entanto, vinte vezes mais bastonetes do que cones na retina porque os bastonetes estão presentes em uma área mais ampla. Devido à sua distribuição mais ampla, os bastonetes são responsáveis ​​pela visão periférica .

Em contraste, as células cone são menos sensíveis à intensidade geral da luz, mas vêm em três variedades que são sensíveis a diferentes faixas de frequência e, portanto, são usadas na percepção de cores e visão fotópica . As células cone são altamente concentradas na fóvea e têm uma alta acuidade visual, o que significa que são melhores em resolução espacial do que os bastonetes. Como os cones não são tão sensíveis à luz fraca quanto os bastonetes, a maior parte da visão noturna é limitada aos bastonetes. Da mesma forma, uma vez que os cones estão na fóvea, a visão central (incluindo a visão necessária para fazer a maior parte da leitura, trabalhos detalhados como costura ou exame cuidadoso de objetos) é feita por cones.

Os músculos ciliares ao redor da lente permitem que o foco do olho seja ajustado. Este processo é conhecido como acomodação . O ponto próximo e o ponto distante definem as distâncias mais próximas e mais distantes do olho em que um objeto pode ser focalizado com nitidez. Para uma pessoa com visão normal, o ponto distante está localizado no infinito. A localização do ponto próximo depende de quanto os músculos podem aumentar a curvatura da lente e de quão inflexível a lente se tornou com a idade. Optometristas , oftalmologistas e oftalmologistas geralmente consideram um ponto próximo apropriado como sendo mais próximo do que a distância de leitura normal - aproximadamente 25 cm.

Defeitos na visão podem ser explicados usando princípios ópticos. À medida que as pessoas envelhecem, a lente se torna menos flexível e o ponto próximo se afasta do olho, uma condição conhecida como presbiopia . Da mesma forma, as pessoas que sofrem de hipermetropia não podem diminuir a distância focal de suas lentes o suficiente para permitir que objetos próximos sejam visualizados em sua retina. Por outro lado, as pessoas que não conseguem aumentar a distância focal de suas lentes o suficiente para permitir que objetos distantes sejam visualizados na retina sofrem de miopia e têm um ponto distante consideravelmente mais próximo do que o infinito. Uma condição conhecida como astigmatismo ocorre quando a córnea não é esférica, mas sim mais curvada em uma direção. Isso faz com que os objetos estendidos horizontalmente sejam focados em diferentes partes da retina do que os objetos estendidos verticalmente e resulta em imagens distorcidas.

Todas essas condições podem ser corrigidas usando lentes corretivas . Para presbiopia e hipermetropia, uma lente convergente fornece a curvatura extra necessária para aproximar o ponto próximo do olho, enquanto para miopia uma lente divergente fornece a curvatura necessária para enviar o ponto distante ao infinito. O astigmatismo é corrigido com uma lente de superfície cilíndrica que se curva mais fortemente em uma direção do que em outra, compensando a não uniformidade da córnea.

A potência ótica das lentes corretivas é medida em dioptrias , valor igual ao recíproco da distância focal medida em metros; com uma distância focal positiva correspondente a uma lente convergente e uma distância focal negativa correspondente a uma lente divergente. Para lentes que também corrigem o astigmatismo, são dados três números: um para a potência esférica, um para a potência cilíndrica e um para o ângulo de orientação do astigmatismo.

Efeitos visuais

A Ilusão do Ponzo baseia-se no fato de que as linhas paralelas parecem convergir quando se aproximam do infinito.

As ilusões de ótica (também chamadas de ilusões visuais) são caracterizadas por imagens visualmente percebidas que diferem da realidade objetiva. A informação recolhida pelo olho é processada no cérebro para dar uma percepção que difere do objeto que está sendo visualizado. As ilusões de ótica podem ser o resultado de uma variedade de fenômenos, incluindo efeitos físicos que criam imagens diferentes dos objetos que as produzem, os efeitos fisiológicos nos olhos e no cérebro de estimulação excessiva (por exemplo, brilho, inclinação, cor, movimento) e ilusões cognitivas onde o olho e o cérebro fazem inferências inconscientes .

As ilusões cognitivas incluem algumas que resultam da má aplicação inconsciente de certos princípios ópticos. Por exemplo, as ilusões da sala Ames , Hering , Müller-Lyer , Orbison , Ponzo , Sander e Wundt dependem todas da sugestão da aparência de distância usando linhas convergentes e divergentes, da mesma forma que raios de luz paralelos (ou mesmo qualquer conjunto de linhas paralelas) parecem convergir em um ponto de fuga no infinito em imagens bidimensionais com perspectiva artística. Essa sugestão também é responsável pela famosa ilusão da lua , onde a lua, apesar de ter essencialmente o mesmo tamanho angular, parece muito maior perto do horizonte do que no zênite . Essa ilusão confundiu tanto Ptolomeu que ele a atribuiu incorretamente à refração atmosférica quando a descreveu em seu tratado Óptica .

Outro tipo de ilusão de ótica explora padrões quebrados para induzir a mente a perceber simetrias ou assimetrias que não estão presentes. Os exemplos incluem a parede do café , Ehrenstein , espiral de Fraser , Poggendorff e ilusões de Zöllner . Relacionados, mas não estritamente ilusórios, estão os padrões que ocorrem devido à sobreposição de estruturas periódicas. Por exemplo, tecidos transparentes com uma estrutura de grade produzem formas conhecidas como padrões moiré , enquanto a sobreposição de padrões transparentes periódicos compreendendo linhas opacas paralelas ou curvas produz padrões de linha moiré .

Instrumentos ópticos

Ilustrações de vários instrumentos ópticos da Cyclopaedia de 1728

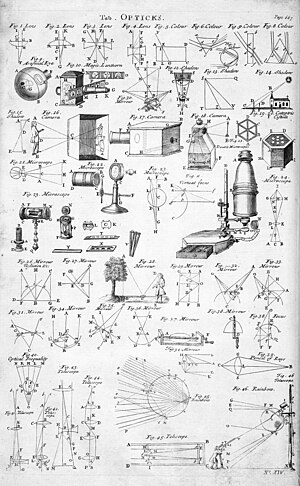
As lentes individuais têm uma variedade de aplicações, incluindo lentes fotográficas , lentes corretivas e lupas, enquanto os espelhos individuais são usados ​​em refletores parabólicos e espelhos retrovisores . A combinação de vários espelhos, prismas e lentes produz instrumentos ópticos compostos que têm usos práticos. Por exemplo, um periscópio é simplesmente dois espelhos planos alinhados para permitir a visualização ao redor de obstruções. Os instrumentos ópticos compostos mais famosos da ciência são o microscópio e o telescópio, ambos inventados pelos holandeses no final do século XVI.

Os microscópios foram desenvolvidos pela primeira vez com apenas duas lentes: uma lente objetiva e uma ocular . A lente objetiva é essencialmente uma lupa e foi projetada com uma distância focal muito pequena, enquanto a ocular geralmente tem uma distância focal maior. Isso tem o efeito de produzir imagens ampliadas de objetos próximos. Geralmente, uma fonte adicional de iluminação é usada, pois as imagens ampliadas são mais escuras devido à conservação de energia e à propagação dos raios de luz sobre uma área de superfície maior. Os microscópios modernos, conhecidos como microscópios compostos, possuem muitas lentes (normalmente quatro) para otimizar a funcionalidade e aumentar a estabilidade da imagem. Uma variedade ligeiramente diferente de microscópio, o microscópio de comparação , analisa imagens lado a lado para produzir uma visão binocular estereoscópica que parece tridimensional quando usada por humanos.

Os primeiros telescópios, chamados de telescópios refratários, também foram desenvolvidos com uma única objetiva e lente ocular. Em contraste com o microscópio, a lente objetiva do telescópio foi projetada com uma grande distância focal para evitar aberrações ópticas. A objetiva focaliza uma imagem de um objeto distante em seu ponto focal, que é ajustado para estar no ponto focal de uma ocular de distância focal muito menor. O objetivo principal de um telescópio não é necessariamente a ampliação, mas sim a coleta de luz que é determinada pelo tamanho físico da lente objetiva. Assim, os telescópios são normalmente indicados pelos diâmetros de suas objetivas, e não pela ampliação que pode ser alterada trocando as oculares. Como a ampliação de um telescópio é igual à distância focal da objetiva dividida pela distância focal da ocular, oculares de menor distância focal causam maior ampliação.

Como fabricar lentes grandes é muito mais difícil do que criar espelhos grandes, a maioria dos telescópios modernos são telescópios refletores , ou seja, telescópios que usam um espelho primário em vez de uma lente objetiva. As mesmas considerações ópticas gerais se aplicam aos telescópios refletores que se aplicam aos telescópios refratores, ou seja, quanto maior o espelho primário, mais luz coletada, e a ampliação ainda é igual à distância focal do espelho primário dividida pela distância focal da ocular. . Os telescópios profissionais geralmente não possuem oculares e, em vez disso, colocam um instrumento (geralmente um dispositivo de carga acoplada) no ponto focal.

Fotografia

Fotografia tirada com abertura f /32

Fotografia tirada com abertura f /5

A ótica da fotografia envolve tanto as lentes quanto o meio no qual a radiação eletromagnética é registrada, seja uma placa , filme ou dispositivo de carga acoplada. Os fotógrafos devem considerar a reciprocidade da câmera e a tomada que é resumida pela relação

Exposição ∝ ApertureArea × ExposureTime × SceneLuminance

Em outras palavras, quanto menor a abertura (dando maior profundidade de foco), menos luz entra, então o período de tempo deve ser aumentado (levando a possível desfoque se ocorrer movimento). Um exemplo do uso da lei da reciprocidade é a regra Sunny 16 , que fornece uma estimativa aproximada das configurações necessárias para estimar a exposição adequada à luz do dia.

A abertura de uma câmera é medida por um número sem unidade chamado número f ou f-stop, f /#, muitas vezes notado como , e dado por ${\displaystyle N}$

${\displaystyle f/\#=N={\frac {f}{D}}\ }$

onde é a distância focal e é o diâmetro da pupila de entrada. Por convenção, " f /#" é tratado como um único símbolo e valores específicos de f /# são escritos substituindo o sinal numérico pelo valor. As duas maneiras de aumentar o f-stop são diminuir o diâmetro da pupila de entrada ou mudar para uma distância focal maior (no caso de uma lente zoom , isso pode ser feito simplesmente ajustando a lente). Números f mais altos também têm uma profundidade de campo maior devido à lente se aproximar do limite de uma câmera pinhole que é capaz de focalizar todas as imagens perfeitamente, independentemente da distância, mas requer tempos de exposição muito longos. ${\displaystyle f}$${\displaystyle D}$

O campo de visão que a lente fornecerá muda com a distância focal da lente. Existem três classificações básicas baseadas na relação entre o tamanho diagonal do filme ou o tamanho do sensor da câmera e a distância focal da lente:

• Lente normal : ângulo de visão de cerca de 50° (denominado normal porque esse ângulo é considerado aproximadamente equivalente à visão humana) e uma distância focal aproximadamente igual à diagonal do filme ou sensor.
• Lente grande angular : ângulo de visão maior que 60° e distância focal menor que uma lente normal.
• Lente de foco longo : ângulo de visão mais estreito que uma lente normal. Esta é qualquer lente com uma distância focal maior que a medida diagonal do filme ou sensor. O tipo mais comum de lente de foco longo é a lente telefoto , um design que usa um grupo especial de telefoto para ser fisicamente mais curto que sua distância focal.

As lentes de zoom modernas podem ter alguns ou todos esses atributos.

O valor absoluto para o tempo de exposição necessário depende de quão sensível à luz é o meio que está sendo usado (medido pela velocidade do filme ou, para mídia digital, pela eficiência quântica ). A fotografia antiga usava mídia com sensibilidade à luz muito baixa e, portanto, os tempos de exposição tinham que ser longos, mesmo para fotos muito brilhantes. À medida que a tecnologia melhorou, também aumentou a sensibilidade por meio de câmeras de filme e câmeras digitais.

Outros resultados da ótica física e geométrica se aplicam à ótica da câmera. Por exemplo, a capacidade máxima de resolução de uma determinada configuração de câmera é determinada pelo limite de difração associado ao tamanho da pupila e dada, aproximadamente, pelo critério de Rayleigh.

Óptica atmosférica

Um céu colorido geralmente se deve à dispersão de luz de partículas e poluição, como nesta fotografia de um pôr do sol durante os incêndios florestais de outubro de 2007 na Califórnia .

As propriedades ópticas únicas da atmosfera causam uma ampla gama de fenômenos ópticos espetaculares. A cor azul do céu é um resultado direto da dispersão de Rayleigh, que redireciona a luz solar de frequência mais alta (azul) de volta ao campo de visão do observador. Como a luz azul se espalha mais facilmente do que a luz vermelha, o sol assume uma tonalidade avermelhada quando é observado através de uma atmosfera espessa, como durante o nascer ou o pôr do sol . Matéria particulada adicional no céu pode espalhar cores diferentes em ângulos diferentes, criando céus coloridos e brilhantes ao entardecer e ao amanhecer. A dispersão de cristais de gelo e outras partículas na atmosfera são responsáveis ​​por halos , brilhos residuais , coroas , raios de sol e cães solares . A variação nesses tipos de fenômenos se deve a diferentes tamanhos e geometrias de partículas.

As miragens são fenômenos ópticos nos quais os raios de luz são desviados devido a variações térmicas no índice de refração do ar, produzindo imagens deslocadas ou fortemente distorcidas de objetos distantes. Outros fenômenos ópticos dramáticos associados a isso incluem o efeito Novaya Zemlya , onde o sol parece nascer mais cedo do que o previsto com uma forma distorcida. Uma forma espetacular de refração ocorre com uma inversão de temperatura chamada Fata Morgana , onde objetos no horizonte ou mesmo além do horizonte, como ilhas, falésias, navios ou icebergs, aparecem alongados e elevados, como "castelos de contos de fadas".

Arco-íris são o resultado de uma combinação de reflexão interna e refração dispersiva da luz nas gotas de chuva. Uma única reflexão nas costas de uma série de gotas de chuva produz um arco-íris com um tamanho angular no céu que varia de 40° a 42° com vermelho do lado de fora. Arco-íris duplos são produzidos por duas reflexões internas com tamanho angular de 50,5° a 54° com violeta do lado de fora. Como os arco-íris são vistos com o sol a 180° de distância do centro do arco-íris, os arco-íris são mais proeminentes quanto mais próximo o sol estiver do horizonte.

Veja também

• óptica de íons
• Publicações importantes em óptica
• Lista de tópicos ópticos

Referências

Leitura adicional

• Nascido, Max; Lobo, Emil (2002). Princípios de Óptica . Cambridge University Press. ISBN 978-1-139-64340-5.
• Hecht, Eugene (2002). Óptica (4 ed.). Addison-Wesley Longman, Incorporated. ISBN 978-0-8053-8566-3.
• Serway, Raymond A.; Jewett, John W. (2004). Física para cientistas e engenheiros (6, edição ilustrada). Belmont, CA: Thomson-Brooks/Cole. ISBN 978-0-534-40842-8.
• Tipler, Paul A.; Mosca, Gene (2004). Física para cientistas e engenheiros: eletricidade, magnetismo, luz e física moderna elementar . Vol. 2. WH Freeman. ISBN 978-0-7167-0810-0.
• Lipson, Stephen G.; Lipson, Henry; Tannhauser, David Stefan (1995). Física Óptica . Cambridge University Press. ISBN 978-0-521-43631-1.
• Fowles, Grant R. (1975). Introdução à Óptica Moderna . Publicações Courier Dover. ISBN 978-0-486-65957-2.

links externos

Discussões relevantes

• Optics em In Our Time na BBC

Livros didáticos e tutoriais

• Light and Matter - um livro de código aberto, contendo um tratamento de óptica no cap. 28-32
• Optics2001 – biblioteca e comunidade de óptica
• Óptica Fundamental – Guia Técnico Melles Griot
• Física da Luz e Óptica - Livro de Graduação da Universidade Brigham Young
• Óptica para PV - uma introdução passo a passo à óptica clássica

Módulos do Wikilivros

Leitura adicional

• Óptica e fotônica: a física aprimorando nossas vidas pelas publicações do Institute of Physics

Sociedades