Operação Módulo - Modulo operation
Na computação , a operação do módulo retorna o resto ou o resto com sinal de uma divisão , depois que um número é dividido por outro (chamado de módulo da operação).
Dados dois números positivos um e n , um modulo n (abreviado como um mod n ) é o resto da divisão euclidiano de um por n , em que uma é o dividendo e n é o divisor . A operação do módulo deve ser distinguida do símbolo mod , que se refere ao módulo (ou divisor) a partir do qual se está operando.
Por exemplo, a expressão "5 mod 2" seria avaliada como 1, porque 5 dividido por 2 tem um quociente de 2 e um resto de 1, enquanto "9 mod 3" seria avaliada como 0, porque a divisão de 9 por 3 tem um quociente de 3 e um restante de 0; não há nada a subtrair de 9 depois de multiplicar 3 por 3.
Embora normalmente executado com a e n sendo ambos inteiros , muitos sistemas de computação agora permitem outros tipos de operandos numéricos. O intervalo de valores para uma operação de módulo inteiro de n é 0 a n - 1 inclusive ( um mod 1 é sempre 0; um mod 0 é indefinido, possivelmente resultando em uma divisão por erro zero em algumas linguagens de programação ). Consulte Aritmética modular para uma convenção mais antiga e relacionada aplicada na teoria dos números .
Quando exatamente um de a ou n é negativo, a definição ingênua falha e as linguagens de programação diferem na forma como esses valores são definidos.
Variantes da definição
Em matemática , o resultado da operação do módulo é uma classe de equivalência e qualquer membro da classe pode ser escolhido como representante ; entretanto, o representante usual é o menor resíduo positivo , o menor inteiro não negativo que pertence àquela classe (isto é, o restante da divisão euclidiana ). No entanto, outras convenções são possíveis. Computadores e calculadoras têm várias maneiras de armazenar e representar números; portanto, sua definição da operação do módulo depende da linguagem de programação ou do hardware subjacente .
Em quase todos os sistemas de computação, o quociente q e o restante r de a dividido por n satisfazem as seguintes condições:
-
( 1 )
No entanto, isso ainda deixa uma ambigüidade de sinal se o resto for diferente de zero: duas escolhas possíveis para o resto ocorrem, uma negativa e outra positiva, e duas escolhas possíveis para o quociente ocorrem. Na teoria dos números, o resto positivo é sempre escolhido, mas na computação, as linguagens de programação escolhem dependendo da linguagem e dos sinais de a ou n . Pascal padrão e ALGOL 68 , por exemplo, fornecem um resto positivo (ou 0) mesmo para divisores negativos, e algumas linguagens de programação, como C90, deixam para a implementação quando n ou a é negativo (consulte a tabela em § Em linguagens de programação para detalhes). um módulo 0 é indefinido na maioria dos sistemas, embora alguns o definam como um .
-
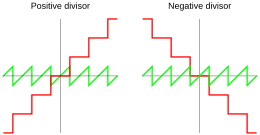
Muitas implementações usam divisão truncada , onde o quociente é definido por truncamento (parte inteira) e, portanto, de acordo com a equação ( 1 ), o restante teria o mesmo sinal do dividendo . O quociente é arredondado para zero: igual ao primeiro inteiro na direção de zero a partir do quociente racional exato.
-
Donald Knuth descreveu a divisão de piso onde o quociente é definido pela função de piso e, portanto, de acordo com a equação ( 1 ), o resto teria o mesmo sinal do divisor . Devido à função floor, o quociente é sempre arredondado para baixo, mesmo que já seja negativo.
-
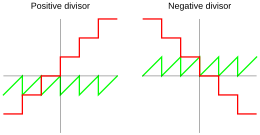
Raymond T. Boute descreve a definição euclidiana em que o resto é sempre não negativo, 0 ≤ r , e é, portanto, consistente com o algoritmo de divisão euclidiana . Nesse caso,
ou equivalente
onde sgn é a função de sinal e, portanto,
- Uma divisão de arredondamento é onde está o quociente , ou seja, arredondado para o número inteiro mais próximo. É encontrado em Common Lisp e IEEE 754 (consulte a rodada para a convenção mais próxima em IEEE-754). Assim, o sinal do resto é escolhido para ser o mais próximo de zero .
- Common Lisp também define a divisão do teto (resto do sinal diferente do divisor) onde o quociente é dado por . Assim, o sinal do resto é escolhido para ser diferente daquele do divisor .
Conforme descrito por Leijen,
Boute argumenta que a divisão euclidiana é superior às outras em termos de regularidade e propriedades matemáticas úteis, embora a divisão por piso, promovida por Knuth, também seja uma boa definição. Apesar de seu uso generalizado, a divisão truncada mostra-se inferior às outras definições.
- Daan Leijen, Divisão e Módulo para Cientistas da Computação
No entanto, a divisão truncada satisfaz a identidade .
Notação
Algumas calculadoras têm um botão de função mod () e muitas linguagens de programação têm uma função semelhante, expressa como mod ( a , n ) , por exemplo. Alguns também oferecem suporte a expressões que usam "%", "mod" ou "Mod" como um módulo ou operador de resto , como a % nou a mod n.
Para ambientes sem uma função semelhante, qualquer uma das três definições acima pode ser usada.
Armadilhas comuns
Quando o resultado de uma operação de módulo tem o sinal do dividendo (definição de truncamento), pode levar a erros surpreendentes.
Por exemplo, para testar se um número inteiro é ímpar , pode-se estar inclinado a testar se o resto por 2 é igual a 1:
bool is_odd(int n) {
return n % 2 == 1;
}
Mas em uma linguagem onde o módulo tem o sinal do dividendo, isso é incorreto, porque quando n (o dividendo) é negativo e ímpar, n mod 2 retorna -1, e a função retorna falso.
Uma alternativa correta é testar se o resto não é 0 (porque o resto 0 é o mesmo, independentemente dos sinais):
bool is_odd(int n) {
return n % 2 != 0;
}
Outra alternativa é usar o fato de que, para qualquer número ímpar, o resto pode ser 1 ou -1:
bool is_odd(int n) {
return n % 2 == 1 || n % 2 == -1;
}
Problemas de desempenho
As operações de módulo podem ser implementadas de forma que uma divisão com um resto seja calculada a cada vez. Para casos especiais, em alguns hardwares, existem alternativas mais rápidas. Por exemplo, o módulo de potências de 2 pode ser expresso alternativamente como uma operação AND bit a bit (assumindo que x é um número inteiro positivo ou usando uma definição não truncada):
x % 2n == x & (2n - 1)
Exemplos:
x % 2 == x & 1x % 4 == x & 3x % 8 == x & 7
Em dispositivos e softwares que implementam operações bit a bit com mais eficiência do que o módulo, essas formas alternativas podem resultar em cálculos mais rápidos.
As otimizações do compilador podem reconhecer expressões da forma expression % constantonde constanté uma potência de dois e implementá-las automaticamente como expression & (constant-1), permitindo ao programador escrever um código mais claro sem comprometer o desempenho. Esta otimização simples não é possível para idiomas nos quais o resultado da operação do módulo tenha o sinal do dividendo (incluindo C ), a menos que o dividendo seja de um tipo inteiro sem sinal. Isso porque, se o dividendo for negativo, o módulo será negativo, expression & (constant-1)mas sempre será positivo. Para essas linguagens, a equivalência deve ser usada, expressa usando operações bit a bit OR, NOT e AND.
x % 2n == x < 0 ? x | ~(2n - 1) : x & (2n - 1)
Otimizações para operações gerais de módulo constante também existem calculando a divisão primeiro usando a otimização de divisor constante .
Propriedades (identidades)
Algumas operações de módulo podem ser fatoradas ou expandidas de forma semelhante a outras operações matemáticas. Isso pode ser útil em provas de criptografia , como a troca de chaves Diffie – Hellman .
- Identidade:
- ( a mod n ) mod n = a mod n .
- n x mod n = 0 para todos os valores inteiros positivos de x .
- Se p é um número primo que não é divisor de b , então ab p −1 mod p = a mod p , devido ao pequeno teorema de Fermat .
- Inverso:
- [(- a mod n ) + ( a mod n )] mod n = 0 .
- b −1 mod n denota o inverso multiplicativo modular , que é definido se e somente se b e n são relativamente primos , que é o caso quando o lado esquerdo é definido: [( b −1 mod n ) ( b mod n ) ] mod n = 1 .
- Distributiva:
- ( a + b ) mod n = [( a mod n ) + ( b mod n )] mod n .
- ab mod n = [( a mod n ) ( b mod n )] mod n .
- Divisão (definição): uma/bmod n = [( a mod n ) ( b −1 mod n )] mod n , quando o lado direito é definido (isto é, quando b e n são coprimos ), e indefinido caso contrário.
- Multiplicação inversa: [( ab mod n ) ( b −1 mod n )] mod n = a mod n .
Em linguagens de programação
| Língua | Operador | Inteiro | Ponto flutuante | Definição |
|---|---|---|---|---|
| ABAP |
MOD
|
sim | sim | Euclidiana |
| ActionScript |
%
|
sim | Não | Truncado |
| Ada |
mod
|
sim | Não | Chão |
rem
|
sim | Não | Truncado | |
| ALGOL 68 |
÷×, mod
|
sim | Não | Euclidiana |
| AMPL |
mod
|
sim | Não | Truncado |
| APL |
|
|
sim | Não | Chão |
| AppleScript |
mod
|
sim | Não | Truncado |
| AutoLISP |
(rem d n)
|
sim | Não | Truncado |
| AWK |
%
|
sim | Não | Truncado |
| BASIC |
Mod
|
sim | Não | Indefinido |
| ac |
%
|
sim | Não | Truncado |
|
C C ++ |
%, div
|
sim | Não | Truncado |
fmod(C) std::fmod(C ++)
|
Não | sim | Truncado | |
remainder(C) std::remainder(C ++)
|
Não | sim | Arredondado | |
| C # |
%
|
sim | sim | Truncado |
| Clarion |
%
|
sim | Não | Truncado |
| Limpar |
rem
|
sim | Não | Truncado |
| Clojure |
mod
|
sim | Não | Chão |
rem
|
sim | Não | Truncado | |
| COBOL |
FUNCTION MOD
|
sim | Não | Chão |
| CoffeeScript |
%
|
sim | Não | Truncado |
%%
|
sim | Não | Chão | |
| Fusão a frio |
%, MOD
|
sim | Não | Truncado |
| Lisp Comum |
mod
|
sim | sim | Chão |
rem
|
sim | sim | Truncado | |
| Cristal |
%
|
sim | Não | Truncado |
| D |
%
|
sim | sim | Truncado |
| Dardo |
%
|
sim | sim | Euclidiana |
remainder()
|
sim | sim | Truncado | |
| Eiffel |
\\
|
sim | Não | Truncado |
| Elixir |
rem/2
|
sim | Não | Truncado |
Integer.mod/2
|
sim | Não | Chão | |
| Olmo |
modBy
|
sim | Não | Chão |
remainderBy
|
sim | Não | Truncado | |
| Erlang |
rem
|
sim | Não | Truncado |
math:fmod/2
|
Não | sim | Truncado (igual a C) | |
| Euforia |
mod
|
sim | Não | Chão |
remainder
|
sim | Não | Truncado | |
| F # |
%
|
sim | sim | Truncado |
| Fator |
mod
|
sim | Não | Truncado |
| FileMaker |
Mod
|
sim | Não | Chão |
| Adiante |
mod
|
sim | Não | Implementação definida |
fm/mod
|
sim | Não | Chão | |
sm/rem
|
sim | Não | Truncado | |
| Fortran |
mod
|
sim | sim | Truncado |
modulo
|
sim | sim | Chão | |
| Frink |
mod
|
sim | Não | Chão |
| GLSL |
%
|
sim | Não | Indefinido |
mod
|
Não | sim | Chão | |
| GameMaker Studio (GML) |
mod, %
|
sim | Não | Truncado |
| GDScript (Godot) |
%
|
sim | Não | Truncado |
fmod
|
Não | sim | Truncado | |
posmod
|
sim | Não | Chão | |
fposmod
|
Não | sim | Chão | |
| Ir |
%
|
sim | Não | Truncado |
math.Mod
|
Não | sim | Truncado | |
| Groovy |
%
|
sim | Não | Truncado |
| Haskell |
mod
|
sim | Não | Chão |
rem
|
sim | Não | Truncado | |
Data.Fixed.mod'( GHC )
|
Não | sim | Chão | |
| Haxe |
%
|
sim | Não | Truncado |
| HLSL |
%
|
sim | sim | Indefinido |
| J |
|
|
Yes | Não | Chão |
| Java |
%
|
sim | sim | Truncado |
Math.floorMod
|
sim | Não | Chão | |
|
JavaScript TypeScript |
%
|
sim | sim | Truncado |
| Julia |
mod
|
sim | Não | Chão |
%, rem
|
sim | Não | Truncado | |
| Kotlin |
%, rem
|
sim | sim | Truncado |
mod
|
sim | sim | Chão | |
| ksh |
%
|
sim | Não | Truncado (igual a POSIX sh) |
fmod
|
Não | sim | Truncado | |
| LabVIEW |
mod
|
sim | sim | Truncado |
| LibreOffice |
=MOD()
|
sim | Não | Chão |
| Logotipo |
MODULO
|
sim | Não | Chão |
REMAINDER
|
sim | Não | Truncado | |
| Lua 5 |
%
|
sim | sim | Chão |
| Lua 4 |
mod(x,y)
|
sim | sim | Truncado |
| Liberty BASIC |
MOD
|
sim | Não | Truncado |
| Mathcad |
mod(x,y)
|
sim | Não | Chão |
| Bordo |
e mod m (por padrão), modp(e, m)
|
sim | Não | Euclidiana |
mods(e, m)
|
sim | Não | Arredondado | |
frem(e, m)
|
sim | sim | Arredondado | |
| Mathematica |
Mod[a, b]
|
sim | Não | Chão |
| MATLAB |
mod
|
sim | Não | Chão |
rem
|
sim | Não | Truncado | |
| Maxima |
mod
|
sim | Não | Chão |
remainder
|
sim | Não | Truncado | |
| Maya Embedded Language |
%
|
sim | Não | Truncado |
| Microsoft Excel |
=MOD()
|
sim | sim | Chão |
| Minitab |
MOD
|
sim | Não | Chão |
| Modula-2 |
MOD
|
sim | Não | Chão |
REM
|
sim | Não | Truncado | |
| CAXUMBA |
#
|
sim | Não | Chão |
| Netwide Assembler ( NASM , NASMX ) |
%, div(sem sinal)
|
sim | Não | N / D |
%% (assinado)
|
sim | Não | Definido pela implementação | |
| Nim |
mod
|
sim | Não | Truncado |
| Oberon |
MOD
|
sim | Não | Chão |
| Objective-C |
%
|
sim | Não | Truncado (igual a C99) |
| Object Pascal , Delphi |
mod
|
sim | Não | Truncado |
| OCaml |
mod
|
sim | Não | Truncado |
mod_float
|
Não | sim | Truncado | |
| Occam |
\
|
sim | Não | Truncado |
| Pascal (ISO-7185 e -10206) |
mod
|
sim | Não | Como euclidiano |
| Código de Programação Avançada ( PCA ) |
\
|
sim | Não | Indefinido |
| Perl |
%
|
sim | Não | Chão |
POSIX::fmod
|
Não | sim | Truncado | |
| Phix |
mod
|
sim | Não | Chão |
remainder
|
sim | Não | Truncado | |
| PHP |
%
|
sim | Não | Truncado |
fmod
|
Não | sim | Truncado | |
| PIC BASIC Pro |
\\
|
sim | Não | Truncado |
| PL / I |
mod
|
sim | Não | Com piso (ANSI PL / I) |
| PowerShell |
%
|
sim | Não | Truncado |
| Código de Programação ( PRC ) |
MATH.OP - 'MOD; (\)'
|
sim | Não | Indefinido |
| Progresso |
modulo
|
sim | Não | Truncado |
| Prolog ( ISO 1995 ) |
mod
|
sim | Não | Chão |
rem
|
sim | Não | Truncado | |
| PureBasic |
%, Mod(x,y)
|
sim | Não | Truncado |
| PureScript |
`mod`
|
sim | Não | Chão |
| Pure Data |
%
|
sim | Não | Truncado (igual a C) |
mod
|
sim | Não | Chão | |
| Pitão |
%
|
sim | sim | Chão |
math.fmod
|
Não | sim | Truncado | |
| Q # |
%
|
sim | Não | Truncado |
| R |
%%
|
sim | Não | Chão |
| Raquete |
modulo
|
sim | Não | Chão |
remainder
|
sim | Não | Truncado | |
| Raku |
%
|
Não | sim | Chão |
| RealBasic |
MOD
|
sim | Não | Truncado |
| Razão |
mod
|
sim | Não | Truncado |
| Rexx |
//
|
sim | sim | Truncado |
| RPG |
%REM
|
sim | Não | Truncado |
| Rubi |
%, modulo()
|
sim | sim | Chão |
remainder()
|
sim | sim | Truncado | |
| Ferrugem |
%
|
sim | sim | Truncado |
rem_euclid()
|
sim | sim | Euclidiana | |
| SAS |
MOD
|
sim | Não | Truncado |
| Scala |
%
|
sim | Não | Truncado |
| Esquema |
modulo
|
sim | Não | Chão |
remainder
|
sim | Não | Truncado | |
| Esquema R 6 RS |
mod
|
sim | Não | Euclidiana |
mod0
|
sim | Não | Arredondado | |
flmod
|
Não | sim | Euclidiana | |
flmod0
|
Não | sim | Arredondado | |
| Arranhar |
mod
|
sim | Não | Chão |
mod
|
Não | sim | Truncado | |
| Seed7 |
mod
|
sim | sim | Chão |
rem
|
sim | sim | Truncado | |
| SenseTalk |
modulo
|
sim | Não | Chão |
rem
|
sim | Não | Truncado | |
sh(POSIX) (inclui bash , mksh , etc.)
|
%
|
sim | Não | Truncado (igual a C) |
| Conversa fiada |
\\
|
sim | Não | Chão |
rem:
|
sim | Não | Truncado | |
| Foto! |
mod
|
sim | Não | Chão |
| Rodar |
//
|
sim | Não | Chão |
| Solidez |
%
|
sim | Não | Chão |
| SQL ( SQL: 1999 ) |
mod(x,y)
|
sim | Não | Truncado |
| SQL ( SQL: 2011 ) |
%
|
sim | Não | Truncado |
| ML padrão |
mod
|
sim | Não | Chão |
Int.rem
|
sim | Não | Truncado | |
Real.rem
|
Não | sim | Truncado | |
| Stata |
mod(x,y)
|
sim | Não | Euclidiana |
| Rápido |
%
|
sim | Não | Truncado |
truncatingRemainder(dividingBy:)
|
Não | sim | Truncado | |
| Tcl |
%
|
sim | Não | Chão |
| Torque |
%
|
sim | Não | Truncado |
| Turing |
mod
|
sim | Não | Chão |
| Verilog (2001) |
%
|
sim | Não | Truncado |
| VHDL |
mod
|
sim | Não | Chão |
rem
|
sim | Não | Truncado | |
| VimL |
%
|
sim | Não | Truncado |
| Visual básico |
Mod
|
sim | Não | Truncado |
| WebAssembly |
i32.rem_s, i64.rem_s
|
sim | Não | Truncado |
| montagem x86 |
IDIV
|
sim | Não | Truncado |
| XBase ++ |
%
|
sim | sim | Truncado |
Mod()
|
sim | sim | Chão | |
| Provador de teorema Z3 |
div, mod
|
sim | Não | Euclidiana |
Além disso, muitos sistemas de computador fornecem uma divmodfuncionalidade que produz o quociente e o restante ao mesmo tempo. Exemplos incluem a arquitetura x86 de IDIVinstrução, da linguagem de programação C div()função, e Python 's divmod()função.
Generalizações
Módulo com deslocamento
Às vezes é útil que o resultado de um módulo n não esteja entre 0 e n - 1 , mas entre algum número d e d + n - 1 . Nesse caso, d é chamado de deslocamento. Não parece haver uma notação padrão para esta operação, portanto, vamos usar um mod d n . Temos, portanto, a seguinte definição: x = a mod d n apenas no caso de d ≤ x ≤ d + n - 1 e x mod n = a mod n . Claramente, a operação usual do módulo corresponde ao deslocamento de zero: a mod n = a mod 0 n . A operação do módulo com deslocamento está relacionada à função de piso da seguinte forma:
(Para ver isso, vamos . Primeiro mostramos que x mod n = a mod n . Em geral, é verdade que ( a + bn ) mod n = a mod n para todos os inteiros b ; portanto, isso também é verdadeiro no caso caso em que ; mas isso significa que , que é o que queríamos provar. Resta ser mostrado que d ≤ x ≤ d + n - 1. Sejam k e r os inteiros tais que a - d = kn + r com 0 ≤ r ≤ n - 1 (ver divisão euclidiana ). Então , assim . Agora pegue 0 ≤ r ≤ n - 1 e adicione d a ambos os lados, obtendo d ≤ d + r ≤ d + n - 1. Mas nós vimos que x = d + r , então terminamos. □)
O módulo com deslocamento a mod d n é implementado no Mathematica como Mod[a, n, d] .
Implementar outras definições de módulo usando truncamento
Apesar da elegância matemática da divisão de Knuth e da divisão euclidiana, é geralmente muito mais comum encontrar um módulo baseado em divisão truncado em linguagens de programação. Leijen fornece os seguintes algoritmos para calcular as duas divisões, dada uma divisão inteira truncada:
/* Euclidean and Floored divmod, in the style of C's ldiv() */
typedef struct {
/* This structure is part of the C stdlib.h, but is reproduced here for clarity */
long int quot;
long int rem;
} ldiv_t;
/* Euclidean division */
inline ldiv_t ldivE(long numer, long denom) {
/* The C99 and C++11 languages define both of these as truncating. */
long q = numer / denom;
long r = numer % denom;
if (r < 0) {
if (denom > 0) {
q = q - 1;
r = r + denom;
} else {
q = q + 1;
r = r - denom;
}
}
return (ldiv_t){.quot = q, .rem = r};
}
/* Floored division */
inline ldiv_t ldivF(long numer, long denom) {
long q = numer / denom;
long r = numer % denom;
if ((r > 0 && denom < 0) || (r < 0 && denom > 0)) {
q = q - 1;
r = r + denom;
}
return (ldiv_t){.quot = q, .rem = r};
}
Observe que, para ambos os casos, o resto pode ser calculado independentemente do quociente, mas não vice-versa. As operações são combinadas aqui para economizar espaço na tela, pois as ramificações lógicas são as mesmas.
Veja também
- Módulo (desambiguação) e módulo (jargão) - muitos usos da palavra módulo , todos originados da introdução da aritmética modular de Carl F. Gauss em 1801.
- Módulo (matemática) , uso geral do termo em matemática
- Exponenciação modular
- Vire (unidade)
Notas
Referências
links externos
- Modulorama , animação de uma representação cíclica de tabuada (explicação em francês)