Algoritmo π de Liu Hui -Liu Hui's π algorithm

Método de Liu Hui para calcular a área de um círculo

O algoritmo π de Liu Hui foi inventado por Liu Hui (fl. Século III), um matemático do Reino de Cao Wei . Antes de sua época, a razão entre a circunferência de um círculo e seu diâmetro era frequentemente considerada experimentalmente como três na China, enquanto Zhang Heng (78-139) a traduziu como 3,1724 (da proporção do círculo celestial para o diâmetro da terra , 92/29 ) ou como . Liu Hui não ficou satisfeito com esse valor. Ele comentou que era muito grande e ultrapassou a marca. Outro matemático Wang Fan (219–257) forneceu π ≈ 142/45 ≈ 3,156 . Todos esses valores empíricos π foram precisos até dois dígitos (ou seja, uma casa decimal). Liu Hui foi o primeiro matemático chinês a fornecer um algoritmo rigoroso para o cálculo de π com qualquer precisão. O cálculo do próprio Liu Hui com um 96-gon forneceu uma precisão de cinco dígitos: π ≈ 3,1416 . ${\ displaystyle \ pi \ approx {\ sqrt {10}} \ approx 3.162}$

Liu Hui observou em seu comentário aos Nove Capítulos sobre a Arte Matemática , que a razão entre a circunferência de um hexágono inscrito e o diâmetro do círculo era três, portanto, π deve ser maior do que três. Ele passou a fornecer uma descrição detalhada passo a passo de um algoritmo iterativo para calcular π com qualquer precisão necessária com base em polígonos bisseccionados; ele calculou π entre 3,141024 e 3,142708 com um 96-gon; ele sugeriu que 3,14 era uma aproximação boa o suficiente e expressou π como 157/50; ele admitiu que esse número era um pouco pequeno. Mais tarde, ele inventou um método rápido e engenhoso para melhorá-lo e obteve π ≈ 3,1416 com apenas um 96-gon, com uma precisão comparável à de um 1536-gon. Sua contribuição mais importante nessa área foi seu algoritmo iterativo π simples.

Área de um círculo

A área dentro de um círculo é igual ao raio multiplicado pela metade da circunferência, ou A = r x C / 2 = r x r x π .

Liu Hui argumentou:

" Multiplique um lado de um hexágono pelo raio (de seu círculo circunflexo) e, em seguida, multiplique por três, para obter a área de um dodecágono; se cortarmos um hexágono em um dodecágono, multiplique seu lado por seu raio e, em seguida, multiplique novamente por seis, obtemos a área de um 24-gon; quanto mais fino cortarmos, menor será a perda em relação à área do círculo, o

Além disso, Liu Hui provou que a área de um círculo é a metade de sua circunferência multiplicada por seu raio. Ele disse:

“ Entre um polígono e um círculo, existe um raio excedente. Multiplique o raio excedente por um lado do polígono. A área resultante excede o limite do círculo ”.

No diagrama d = raio excedente. Multiplicar d por um lado resulta em ABCD oblongo que excede o limite do círculo. Se um lado do polígono for pequeno (ou seja, se houver um grande número de lados), o raio excedente será pequeno, portanto, a área excedente será pequena.

Como no diagrama, quando N → ∞ , d → 0 e ABCD → 0 .

" Multiplique o lado de um polígono por seu raio e a área dobra; portanto, multiplique metade da circunferência pelo raio para obter a área do círculo ".

Quando N → ∞ , metade da circunferência do N -gon se aproxima de um semicírculo, portanto, metade da circunferência de um círculo multiplicada por seu raio é igual à área do círculo. Liu Hui não explicou em detalhes essa dedução. No entanto, é evidente ao usar o "princípio do complemento para dentro e para fora" de Liu Hui, que ele forneceu em outro lugar nos Nove Capítulos sobre a Arte Matemática : Corte uma forma geométrica em partes, reorganize as partes para formar outra forma, a área do duas formas serão idênticas.

Assim, reorganizando os seis triângulos verdes, três triângulos azuis e três triângulos vermelhos em um retângulo com largura = 3 L e altura R mostra que a área do dodecágono = 3 RL .

Em geral, multiplicar metade da circunferência de um N- gon pelo seu raio resulta na área de 2 N -gon. Liu Hui usou esse resultado repetidamente em seu algoritmo π .

Desigualdade π de Liu Hui

Desigualdade π de Liu Hui

Liu Hui provou uma desigualdade envolvendo π ao considerar a área dos polígonos inscritos com N e 2 N lados.

No diagrama, a área amarela representa a área de um N -gon, denotada por , e a área amarela mais a área verde representa a área de 2 N -gon, denotada por . Portanto, a área verde representa a diferença entre as áreas do 2 N -gon e do N -gon: ${\ displaystyle A_ {N}}$${\ displaystyle A_ {2N}}$

${\ displaystyle D_ {2N} = A_ {2N} -A_ {N}.}$

A área vermelha é igual à área verde e também . Então ${\ displaystyle D_ {2N}}$

Área amarela + área verde + área vermelha = ${\ displaystyle A_ {2N} + D_ {2N}.}$

Deixe representar a área do círculo. Então ${\ displaystyle A_ {C}}$

${\ displaystyle A_ {2N} <A_ {C} <A_ {2N} + D_ {2N}.}$

Se o raio do círculo for considerado 1, então temos a desigualdade π de Liu Hui :

${\ displaystyle A_ {2N} <\ pi <A_ {2N} + D_ {2N}.}$

Algoritmo iterativo

Algoritmo π de Liu Hui

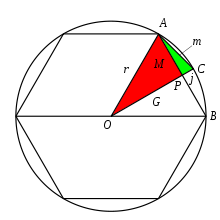
Liu Hui começou com um hexágono inscrito. Seja M o comprimento de um lado AB do hexágono, r é o raio do círculo.

Divida AB com a linha OPC , AC torna-se um lado do dodecágono (12-gon), deixe seu comprimento ser m . Deixe o comprimento do PC ser j eo comprimento do OP seja G .

AOP , APC são dois triângulos retângulos. Liu Hui usou o teorema de Pitágoras repetidamente:

${\ displaystyle {} G ^ {2} = r ^ {2} - \ left ({\ tfrac {M} {2}} \ right) ^ {2}}$

${\ displaystyle {} G = {\ sqrt {r ^ {2} - {\ tfrac {M ^ {2}} {4}}}}}$

${\ displaystyle {} j = rG = r - {\ sqrt {r ^ {2} - {\ tfrac {M ^ {2}} {4}}}}}$

${\ displaystyle {} m ^ {2} = \ left ({\ tfrac {M} {2}} \ right) ^ {2} + j ^ {2}}$

${\ displaystyle {} m = {\ sqrt {\ left ({\ tfrac {M} {2}} \ right) ^ {2} + j ^ {2}}}}$

${\ displaystyle {} m = {\ sqrt {\ left ({\ tfrac {M} {2}} \ right) ^ {2} + \ left (rG \ right) ^ {2}}}}$

${\ displaystyle {} m = {\ sqrt {\ left ({\ tfrac {M} {2}} \ right) ^ {2} + \ left (r - {\ sqrt {r ^ {2} - {\ tfrac {M ^ {2}} {4}}}} \ right) ^ {2}}}}$

A partir daqui, existe agora uma técnica para determinar m de M , que fornece o comprimento lateral de um polígono com duas vezes o número de arestas. Começando com um hexágono , Liu Hui poderia determinar o comprimento lateral de um dodecágono usando esta fórmula. Em seguida, continue repetidamente para determinar o comprimento lateral de um icositetrágono dado o comprimento lateral de um dodecágono. Ele poderia fazer isso recursivamente quantas vezes forem necessárias. Sabendo como determinar a área desses polígonos, Liu Hui poderia então aproximar π .

Com unidades, ele obteve ${\ displaystyle r = 10}$

área de 48 gon ${\ displaystyle {} A_ {96} = 313 {584 \ over 625}}$

área de 96 gon ${\ displaystyle {} A_ {192} = 314 {64 \ over 625}}$

Diferença de 96 gon e 48 gon:

${\ displaystyle {} D_ {192} = 314 {\ frac {64} {625}} - 313 {\ frac {584} {625}} = {\ frac {105} {625}}}$

da desigualdade π de Liu Hui :

${\ displaystyle A_ {2N} <A_ {C} <A_ {2N} + D_ {2N}.}$

Uma vez que r = 10,${\ displaystyle A_ {C} = 100 \ vezes \ pi}$

portanto:

${\ displaystyle {} 314 {\ frac {64} {625}} <100 \ vezes \ pi <314 {\ frac {64} {625}} + {\ frac {105} {625}}}$

${\ displaystyle {} 314 {\ frac {64} {625}} <100 \ vezes \ pi <314 {\ frac {169} {625}}}$

${\ displaystyle {} 3,141024 <\ pi <3,142704.}$

Ele nunca considerou π como a média do limite inferior 3,141024 e do limite superior 3,142704. Em vez disso, ele sugeriu que 3,14 era uma aproximação boa o suficiente para π , e o expressou como uma fração ; ele apontou que este número é ligeiramente menor que o valor real de π . ${\ displaystyle {\ tfrac {157} {50}}}$

Liu Hui realizou seus cálculos com cálculo de bastão e expressou seus resultados com frações. No entanto, a natureza iterativa do algoritmo π de Liu Hui é bastante clara:

${\ displaystyle 2-m ^ {2} = {\ sqrt {2+ (2-M ^ {2})}} \ ,,}$

em que m é o comprimento de um dos lados do polígono-próxima ordem bissectada a partir de H . O mesmo cálculo é feito repetidamente, cada etapa exigindo apenas uma adição e uma extração de raiz quadrada.

Método rápido

O cálculo de raízes quadradas de números irracionais não era uma tarefa fácil no século III com a contagem de barras . Liu Hui descobriu um atalho comparando os diferenciais de área dos polígonos e descobriu que a proporção da diferença na área de polígonos de ordem sucessiva era de aproximadamente 1/4.

Deixe D _N denotar a diferença nas áreas de N -gon e ( N / 2) -gon

${\ displaystyle D_ {N} = A_ {N} -A_ {N / 2} \,}$

Ele encontrou:

${\ displaystyle D_ {96} \ approx {\ tfrac {1} {4}} D_ {48}}$

${\ displaystyle D_ {192} \ approx {\ tfrac {1} {4}} D_ {96}}$

Por isso:

${\ displaystyle {\ begin {alinhados} D_ {384} & {} \ approx {\ tfrac {1} {4}} D_ {192} \\ D_ {768} & {} \ approx \ left ({\ tfrac { 1} {4}} \ direita) ^ {2} D_ {192} \\ D_ {1536} & {} \ aprox \ esquerda ({\ tfrac {1} {4}} \ direita) ^ {3} D_ { 192} \\ D_ {3072} & {} \ approx \ left ({\ tfrac {1} {4}} \ right) ^ {4} D_ {192} \\ & {} \ \ \ vdots \ end {alinhados }}}$

Área do círculo de raio unitário =

${\ displaystyle {} \ pi = A_ {192} + D_ {384} + D_ {768} + D_ {1536} + D_ {3072} + \ cdots \ approx A_ {192} + F \ cdot D_ {192}. \,}$

No qual

${\ displaystyle F = {\ tfrac {1} {4}} + \ left ({\ tfrac {1} {4}} \ right) ^ {2} + \ left ({\ tfrac {1} {4}} \ right) ^ {3} + \ left ({\ tfrac {1} {4}} \ right) ^ {4} + \ cdots = {\ frac {\ frac {1} {4}} {1 - {\ frac {1} {4}}}} = {\ tfrac {1} {3}}.}$

Ou seja, todas as áreas excedentes subsequentes somam um terço do ${\ displaystyle D_ {192}}$

área do círculo unitário${\ displaystyle {} = \ pi \ approx A_ {192} + \ left ({\ tfrac {1} {3}} \ right) D_ {192} \ approx {3927 \ over 1250} \ approx 3,1416. \,}$

Liu Hui ficou muito feliz com este resultado, pois havia obtido o mesmo resultado com o cálculo para um gon de 1536, obtendo a área de um gon de 3072. Isso explica quatro questões:

1. Por que ele parou em A ₁₉₂ em sua apresentação de seu algoritmo. Porque ele descobriu um método rápido de melhorar a precisão de π , obtendo o mesmo resultado de 1536-gon com apenas 96-gon. Afinal, o cálculo de raízes quadradas não era uma tarefa simples com cálculo de bastão . Com o método rápido, ele só precisava realizar mais uma subtração, mais uma divisão (por 3) e mais uma adição, em vez de mais quatro extrações de raiz quadrada.
2. Por que ele preferiu calcular π através do cálculo de áreas em vez de circunferências de polígonos sucessivos, porque o método rápido exigia informações sobre a diferença em áreas de polígonos sucessivos.
3. Quem foi o verdadeiro autor do parágrafo contendo cálculo de ${\ displaystyle \ pi = {3927 \ over 1250}.}$
4. Esse famoso parágrafo começava com "Um contêiner de bronze da dinastia Han no armazém militar da dinastia Jin ...". Muitos estudiosos, entre eles Yoshio Mikami e Joseph Needham , acreditavam que o parágrafo do "recipiente de bronze da dinastia Han" era obra de Liu Hui e não de Zu Chongzhi como outros acreditavam, devido à forte correlação dos dois métodos por meio de cálculo de área e porque não houve uma única palavra mencionando o resultado de Zu 3,1415926 < π <3,1415927 obtido por meio de 12288-gon.

Desenvolvimentos posteriores

Liu Hui estabeleceu um algoritmo sólido para cálculo de π com qualquer precisão.

• Zu Chongzhi estava familiarizado com o trabalho de Liu Hui e obteve maior precisão aplicando seu algoritmo a um 12288-gon.

Da fórmula de Liu Hui para 2 N -gon:

${\ displaystyle A_ {2N} = m_ {N} \ vezes r}$

Para 12288-gon inscrito em um círculo de raio unitário:

${\ displaystyle A_ {24576} = 3,14159261864 <\ pi}$.

Da desigualdade π de Liu Hui :

${\ displaystyle A_ {24576} <\ pi <A_ {24576} + D_ {24576}}$

No qual ${\ displaystyle D_ {24576} = A_ {24576} -A_ {12288} = 0,0000001021}$

${\ displaystyle A_ {24576} = 3,14159261864 <\ pi <3,14159261864 + 0,0000001021}$.

Portanto

${\ displaystyle 3,14159261864 <\ pi <3,141592706934}$

Truncado para oito dígitos significativos:

${\ displaystyle 3,1415926 <\ pi <3,1415927}$.

Essa foi a famosa desigualdade π de Zu Chongzhi .

Zu Chongzhi então usada a fórmula de interpolação por Ele Chengtian (何承天, 370-447) e obteve uma fracção de aproximação: . ${\ displaystyle \ pi \ approx {355 \ over 113}}$

No entanto, este valor π desapareceu na história chinesa por um longo período de tempo (por exemplo, o matemático da dinastia Song Qin Jiushao usou π = e ), até que o matemático da dinastia Yuan Zhao Yuqin trabalhou em uma variação do algoritmo π de Liu Hui , dividindo um quadrado inscrito e obtido novamente${\ displaystyle {22 \ over 7}}$${\ displaystyle \ pi = {\ sqrt {10}})}$${\ displaystyle \ pi \ approx {355 \ over 113}.}$

Significado do algoritmo de Liu Hui

O algoritmo π de Liu Hui foi uma de suas contribuições mais importantes para a matemática chinesa antiga. Foi baseado no cálculo da área de N -gon, em contraste com o algoritmo de Arquimedes baseado na circunferência do polígono. Com este método, Zu Chongzhi obteve o resultado de oito dígitos: 3,1415926 < π <3,1415927, que detinha o recorde mundial para o valor mais preciso de π em 1200 anos, mesmo por volta de 1600 na Europa, o matemático holandês Adriaan Anthonisz e seu filho obtiveram π valor de 3,1415929, com precisão de apenas 7 dígitos.

Veja também

• Método de exaustão
• Algoritmo π de Zhao Youqin

Notas

^ 1 Valor correto: 0,2502009052

^ 2 Valores corretos:

${\ displaystyle A_ {192} = 3,1410319509}$

${\ displaystyle D_ {192} = 0,0016817478}$

${\ displaystyle \ pi \ approx A_ {192} + {\ frac {1} {3}} D_ {192} \ approxeq 3,1410319509 + 0,0016817478 / 3}$

${\ displaystyle \ pi \ approx 3,1410319509 + 0,0005605826}$

${\ displaystyle \ pi \ approx 3.1415925335.}$

O método rápido de Liu Hui foi potencialmente capaz de entregar quase o mesmo resultado de 12288-gon (3,141592516588) com apenas 96-gon.

Referências

Leitura adicional

• Needham, Joseph (1986). Ciência e Civilização na China : Volume 3, Matemática e as Ciências dos Céus e da Terra. Taipei: Caves Books, Ltd.
• Wu Wenjun ed, History of Chinese Mathematics Vol III (em chinês) ISBN  7-303-04557-0