Frustração geométrica - Geometrical frustration

Na física da matéria condensada , o termo frustração geométrica (ou em suma: frustração ) refere-se a um fenômeno onde os átomos tendem a se prender a posições não triviais ou onde, em uma rede de cristal regular , forças interatômicas conflitantes (cada uma favorecendo bastante simples , mas estruturas diferentes) levam a estruturas bastante complexas. Como consequência da frustração na geometria ou nas forças, uma plenitude de estados básicos distintos pode resultar na temperatura zero, e o ordenamento térmico usual pode ser suprimido em temperaturas mais altas. Muitos exemplos estudados são materiais amorfos , vidros ou ímãs diluídos .

O termo frustração , no contexto dos sistemas magnéticos , foi introduzido por Gerard Toulouse (1977). Na verdade, sistemas magnéticos frustrados já haviam sido estudados antes. Os primeiros trabalhos incluem um estudo do modelo de Ising em uma rede triangular com spins vizinhos mais próximos acoplados antiferromagneticamente , por GH Wannier , publicado em 1950. Características relacionadas ocorrem em ímãs com interações concorrentes , onde ambos os acoplamentos ferromagnéticos e antiferromagnéticos entre pares de spins ou momentos magnéticos estão presentes, com o tipo de interação dependendo da distância de separação dos spins. Nesse caso , a comensurabilidade , como arranjos de spin helicoidal , pode resultar, como foi discutido originalmente, especialmente por A. Yoshimori, TA Kaplan, RJ Elliott e outros, a partir de 1959, para descrever achados experimentais em metais de terras raras. Um interesse renovado em tais sistemas de spin com interações frustradas ou concorrentes surgiu cerca de duas décadas depois, começando na década de 1970, no contexto de vidros de spin e superestruturas magnéticas moduladas espacialmente. Em vidros de spin, a frustração é aumentada por desordem estocástica nas interações, como pode ocorrer, experimentalmente, em ligas magnéticas não estequiométricas . Modelos de spin cuidadosamente analisados ​​com frustração incluem o modelo Sherrington-Kirkpatrick , que descreve os vidros de spin, e o modelo ANNNI , que descreve as superestruturas magnéticas de comensurabilidade .

Ordenação magnética

Figura 1: spins interagindo antiferromagneticamente em um arranjo triangular

Figura 2: Spins interagindo antiferromagneticamente em um arranjo tetraédrico

Figura 3: gira ao longo dos eixos fáceis de um tetraedro

Figura 4: Rotações fáceis frustradas em um tetraedro

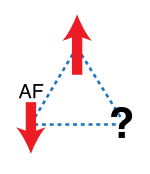
A frustração geométrica é uma característica importante no magnetismo , onde se origina do arranjo relativo dos spins . Um exemplo simples em 2D é mostrado na Figura 1. Três íons magnéticos residem nos cantos de um triângulo com interações antiferromagnéticas entre eles; a energia é minimizada quando cada spin é alinhado em oposição aos vizinhos. Uma vez que os dois primeiros spins se alinham antiparalelos, o terceiro fica frustrado porque suas duas orientações possíveis, para cima e para baixo, fornecem a mesma energia. O terceiro giro não pode minimizar simultaneamente suas interações com os outros dois. Como esse efeito ocorre para cada spin, o estado fundamental é degenerado seis vezes . Apenas os dois estados em que todos os giros são para cima ou para baixo têm mais energia.

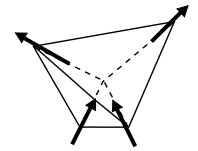
Da mesma forma, em três dimensões, quatro spins dispostos em um tetraedro (Figura 2) podem sofrer frustração geométrica. Se houver uma interação antiferromagnética entre os spins, não será possível organizar os spins de forma que todas as interações entre os spins sejam antiparalelas. Existem seis interações com o vizinho mais próximo, quatro das quais são antiparalelas e, portanto, favoráveis, mas duas das quais (entre 1 e 2 e entre 3 e 4) são desfavoráveis. É impossível ter todas as interações favoráveis ​​e o sistema fica frustrado.

A frustração geométrica também é possível se os spins estiverem dispostos de forma não colinear . Se considerarmos um tetraedro com um spin em cada vértice apontando ao longo do eixo fácil (isto é, diretamente em direção ou longe do centro do tetraedro), então é possível organizar os quatro spins de modo que não haja spin final (Figura 3). Isso é exatamente equivalente a ter uma interação antiferromagnética entre cada par de spins, portanto, neste caso, não há frustração geométrica. Com esses eixos, surge a frustração geométrica se houver uma interação ferromagnética entre vizinhos, onde a energia é minimizada por spins paralelos. O melhor arranjo possível é mostrado na Figura 4, com dois spins apontando para o centro e dois apontando para fora. O momento magnético líquido aponta para cima, maximizando as interações ferromagnéticas nesta direção, mas os vetores esquerdo e direito se cancelam (ou seja, são antiferromagneticamente alinhados), assim como para a frente e para trás. Existem três arranjos equivalentes diferentes com dois spins out e dois in, então o estado fundamental é três vezes degenerado.

Definição matemática

A definição matemática é simples (e análoga ao chamado loop de Wilson na cromodinâmica quântica ): considera-se, por exemplo, expressões ("energias totais" ou "hamiltonianos") da forma

${\ displaystyle {\ mathcal {H}} = \ sum _ {G} -I_ {k _ {\ nu}, k _ {\ mu}} \, \, S_ {k _ {\ nu}} \ cdot S_ {k_ { \ mu}} \ ,,}$

onde G é o gráfico considerado, enquanto as quantidades I _{k ν , k μ} são as chamadas "energias de troca" entre os vizinhos mais próximos, que (nas unidades de energia consideradas) assumem os valores ± 1 (matematicamente, este é um sinal gráfico ), enquanto S _{k ν} · S _{k μ} são produtos internos de spins escalares ou vetoriais ou pseudo-spins. Se o gráfico G tem faces quadráticas ou triangulares P , as chamadas "variáveis ​​de plaqueta" P _W , "produtos de loop" do seguinte tipo, aparecem:

${\ displaystyle P_ {W} = I_ {1,2} \, I_ {2,3} \, I_ {3,4} \, I_ {4,1}}$e respectivamente,${\ displaystyle P_ {W} = I_ {1,2} \, I_ {2,3} \, I_ {3,1} \ ,,}$

que também são chamados de "produtos de frustração". É preciso realizar uma soma sobre esses produtos, somada a todas as placas. O resultado para uma única plaqueta é +1 ou -1. No último caso mencionado, a plaqueta é "geometricamente frustrada".

Pode-se mostrar que o resultado tem uma invariância de calibre simples : ele não muda - nem outras quantidades mensuráveis, por exemplo, a "energia total" - mesmo se localmente as integrais de troca e os spins são modificados simultaneamente da seguinte forma: ${\ displaystyle {\ mathcal {H}}}$

${\ displaystyle I_ {i, k} \ to \ varepsilon _ {i} I_ {i, k} \ varejpsilon _ {k}, \ quad S_ {i} \ to \ varejpsilon _ {i} S_ {i}, \ quad S_ {k} \ a \ varejpsilon _ {k} S_ {k} \ ,.}$

Aqui, os números ε _i e ε _k são sinais arbitrários, ou seja, +1 ou −1, de modo que a estrutura modificada pode parecer totalmente aleatória.

Agua gelada

Figura 5: Esquema de moléculas de gelo de água

Embora a maioria das pesquisas anteriores e atuais sobre frustração se concentrem em sistemas de spin, o fenômeno foi estudado pela primeira vez em gelo comum . Em 1936, Giauque e Stout publicaram A entropia da água e a terceira lei da termodinâmica. Capacidade de Calor do Gelo de 15 K a 273 K , relatando medições do calorímetro na água através das transições de congelamento e vaporização até a fase de gás de alta temperatura. A entropia foi calculada integrando a capacidade de calor e adicionando as contribuições de calor latente ; as medições de baixa temperatura foram extrapoladas para zero, usando a fórmula então recentemente derivada de Debye. A entropia resultante, S ₁  = 44,28 cal / (K · mol) = 185,3 J / (mol · K) foi comparada com o resultado teórico da mecânica estatística de um gás ideal, S ₂  = 45,10 cal / (K · mol) = 188,7 J / (mol · K). Os dois valores diferem por S ₀  = 0,82 ± 0,05 cal / (K · mol) = 3,4 J / (mol · K). Este resultado foi então explicado por Linus Pauling com uma excelente aproximação, que mostrou que o gelo possui uma entropia finita (estimada em 0,81 cal / (K · mol) ou 3,4 J / (mol · K)) à temperatura zero devido à desordem configuracional intrínseco aos prótons no gelo.

Na fase hexagonal ou cúbica de gelo, os íons de oxigênio formam uma estrutura tetraédrica com um comprimento de ligação O – O de 2,76  Å (276  pm ), enquanto o comprimento da ligação O – H mede apenas 0,96 Å (96 pm). Cada íon de oxigênio (branco) é cercado por quatro íons de hidrogênio (preto) e cada íon de hidrogênio é cercado por 2 íons de oxigênio, como mostrado na Figura 5. Mantendo a estrutura da molécula de H ₂ O interna , a posição de energia mínima de um próton não é a meio caminho entre dois íons de oxigênio adjacentes. Existem duas posições equivalentes que um hidrogênio pode ocupar na linha da ligação O – O, uma posição distante e uma próxima. Assim, uma regra leva à frustração das posições do próton para uma configuração de estado fundamental: para cada oxigênio, dois dos prótons vizinhos devem residir na posição distante e dois deles na posição próxima, as chamadas ' regras de gelo '. Pauling propôs que a estrutura tetraédrica aberta do gelo fornece muitos estados equivalentes que satisfazem as regras do gelo.

Pauling passou a calcular a entropia configuracional da seguinte maneira: considere um mol de gelo, consistindo de N O ²⁻ e 2 N prótons. Cada ligação O – O tem duas posições para um próton, levando a 2 ^{2 N} configurações possíveis. No entanto, entre as 16 configurações possíveis associados com cada um deles oxigénio, apenas 6 são energeticamente favorável, mantendo a H ₂ O molécula de restrição. Então, um limite superior dos números que o estado fundamental pode assumir é estimado como Ω  <2 ^{2 N} (6/16) ^N . Correspondentemente, a entropia configuracional S ₀  = k _B ln ( Ω ) = Nk _B ln (3/2) = 0,81 cal / (K · mol) = 3,4 J / (mol · K) está em incrível acordo com a entropia perdida medida por Giauque e Stout.

Embora o cálculo de Pauling tenha negligenciado tanto a restrição global no número de prótons quanto a restrição local decorrente de loops fechados na rede de Wurtzite, a estimativa subsequentemente mostrou ser de excelente precisão.

Gelo giratório

Figura 6: Esquema de spin das moléculas de gelo

Uma situação matematicamente análoga à degenerescência do gelo de água é encontrada nos gelos de spin . Uma estrutura de gelo de rotação comum é mostrada na Figura 6 na estrutura do pirocloro cúbico com um átomo magnético ou íon residindo em cada um dos quatro cantos. Devido ao forte campo de cristal no material, cada um dos íons magnéticos pode ser representado por um par de estado fundamental Ising com um grande momento. Isso sugere uma imagem de spins de Ising residindo na rede tetraédrica de canto compartilhado com spins fixados ao longo do eixo de quantização local, os eixos cúbicos <111> , que coincidem com as linhas que conectam cada vértice tetraédrico ao centro. Cada célula tetraédrica deve ter dois spins apontando para dentro e dois apontando para fora, a fim de minimizar a energia. Atualmente, o modelo de spin ice foi aproximadamente realizado por materiais reais, mais notavelmente os pirocloros de terras raras Ho ₂ Ti ₂ O ₇ , Dy ₂ Ti ₂ O ₇ e Ho ₂ Sn ₂ O ₇ . Todos esses materiais mostram entropia residual diferente de zero em baixa temperatura.

Extensão do modelo de Pauling: Frustração geral

O modelo de spin ice é apenas uma subdivisão dos sistemas frustrados. A palavra frustração foi introduzida inicialmente para descrever a incapacidade de um sistema de minimizar simultaneamente a energia de interação competitiva entre seus componentes. Em geral, a frustração é causada por interações concorrentes devido à desordem do local (ver também o modelo de Vilão ) ou por estrutura de rede, como nas redes triangular , cúbica centrada na face (fcc), hexagonal-compactada , tetraedro , pirocloro e kagome com interação antiferromagnética. Portanto, a frustração é dividida em duas categorias: a primeira corresponde ao vidro giratório , que apresenta tanto desordem na estrutura quanto frustração na rotação; a segunda é a frustração geométrica com uma estrutura de rede ordenada e a frustração de spin. A frustração de um vidro de spin é entendida no âmbito do modelo RKKY , no qual a propriedade de interação, seja ferromagnética ou anti-ferromagnética, depende da distância dos dois íons magnéticos. Devido à desordem de rede no vidro de spin, um spin de interesse e seus vizinhos mais próximos podem estar em distâncias diferentes e ter uma propriedade de interação diferente, o que leva a um alinhamento preferencial diferente do spin.

Ferromagnetos artificiais geometricamente frustrados

Com a ajuda de técnicas de litografia, é possível fabricar ilhas magnéticas de tamanho submicrométrico, cujo arranjo geométrico reproduz a frustração encontrada em materiais de gelo giratório de ocorrência natural. Recentemente, RF Wang et al. relataram a descoberta de um ímã artificial geometricamente frustrado composto de matrizes de ilhas ferromagnéticas de domínio único fabricadas litograficamente. Essas ilhas são organizadas manualmente para criar um análogo bidimensional para girar o gelo. Os momentos magnéticos das ilhas de 'spin' ordenadas foram fotografados com microscopia de força magnética (MFM) e, em seguida, a acomodação local de frustração foi cuidadosamente estudada. Em seu trabalho anterior em uma rede quadrada de ímãs frustrados, eles observaram correlações de curto alcance semelhantes ao gelo e a ausência de correlações de longo alcance, assim como no gelo de spin em baixa temperatura. Esses resultados solidificam o terreno desconhecido no qual a física real da frustração pode ser visualizada e modelada por esses ímãs artificiais geometricamente frustrados e inspira novas atividades de pesquisa.

Esses ferromagnetos artificialmente frustrados podem exibir propriedades magnéticas únicas ao estudar sua resposta global a um campo externo usando o efeito Kerr magneto-óptico. Em particular, uma dependência angular não monotônica da coercividade da rede quadrada é encontrada para estar relacionada à desordem no sistema de gelo artificial de spin.

Frustração geométrica sem rede

Outro tipo de frustração geométrica surge da propagação de uma ordem local. A principal questão que um físico da matéria condensada enfrenta é explicar a estabilidade de um sólido.

Às vezes é possível estabelecer algumas regras locais, de natureza química, que levam a configurações de baixa energia e, portanto, regem a ordem estrutural e química. Geralmente, esse não é o caso e frequentemente a ordem local definida por interações locais não pode se propagar livremente, levando à frustração geométrica. Uma característica comum de todos esses sistemas é que, mesmo com regras locais simples, eles apresentam um grande conjunto de realizações estruturais, muitas vezes complexas. A frustração geométrica desempenha um papel nos campos da matéria condensada, variando de aglomerados e sólidos amorfos a fluidos complexos.

O método geral de abordagem para resolver essas complicações segue duas etapas. Em primeiro lugar, a restrição do preenchimento perfeito do espaço é relaxada, permitindo a curvatura do espaço. Uma estrutura ideal, não frustrada, é definida neste espaço curvo. Em seguida, distorções específicas são aplicadas a este modelo ideal para incorporá-lo no espaço euclidiano tridimensional. A estrutura final é uma mistura de regiões ordenadas, onde a ordem local é semelhante à do template, e defeitos decorrentes da incorporação. Dentre os possíveis defeitos, as divulgações desempenham um papel importante.

O ladrilho de um plano por pentágonos é impossível, mas pode ser realizado em uma esfera na forma de dodecaedro pentagonal, conforme demonstrado em quasicristais

Exemplos bidimensionais simples

Os exemplos bidimensionais são úteis para se obter algum entendimento sobre a origem da competição entre as regras locais e a geometria em geral. Considere primeiro um arranjo de discos idênticos (um modelo para um hipotético metal bidimensional) em um plano; supomos que a interação entre os discos é isotrópica e tende localmente a arranjar os discos da maneira mais densa possível. O melhor arranjo para três discos é trivialmente um triângulo equilátero com os centros dos discos localizados nos vértices do triângulo. O estudo da estrutura de longo alcance pode, portanto, ser reduzido ao das telhas planas com triângulos equiláteros. Uma solução bem conhecida é fornecida pelo ladrilho triangular com total compatibilidade entre as regras locais e globais: o sistema é considerado "não frustrado".

Mas agora, a energia de interação deve ser mínima quando os átomos se situam nos vértices de um pentágono regular . Tentar propagar em longo prazo um empacotamento desses pentágonos compartilhando arestas (ligações atômicas) e vértices (átomos) é impossível. Isso se deve à impossibilidade de colocar lado a lado um plano com pentágonos regulares, simplesmente porque o ângulo do vértice do pentágono não divide 2 π . Três desses pentágonos podem caber facilmente em um vértice comum, mas permanece uma lacuna entre duas arestas. É esse tipo de discrepância que se denomina "frustração geométrica". Existe uma maneira de superar essa dificuldade. Deixe que a superfície a ser ladrilhada esteja livre de qualquer topologia pressuposta e vamos construir a ladrilho com uma aplicação estrita da regra de interação local. Neste exemplo simples, observamos que a superfície herda a topologia de uma esfera e então recebe uma curvatura. A estrutura final, aqui um dodecaedro pentagonal, permite uma propagação perfeita da ordem pentagonal. É chamado de modelo "ideal" (sem defeitos) para a estrutura considerada.

Estruturas densas e embalagens tetraédricas

Empacotamento tetraédrico: O ângulo diedro de um tetraedro não é comensurável com 2 π ; conseqüentemente, permanece um buraco entre duas faces de um empacotamento de cinco tetraedros com uma borda comum. Um empacotamento de vinte tetraedros com um vértice comum de tal forma que os doze vértices externos formam um icosaedro irregular.

A estabilidade dos metais é uma questão de longa data da física do estado sólido, que só pode ser entendida na estrutura da mecânica quântica levando-se em consideração a interação entre os íons carregados positivamente e os elétrons de valência e condução. No entanto, é possível usar uma imagem muito simplificada de ligações metálicas e manter apenas um tipo de interação isotrópica, originando estruturas que podem ser representadas como esferas densamente compactadas. E, de fato, as estruturas de metal simples cristalinas são freqüentemente ou cúbicas de face centrada (fcc) ou reticulados de empacotamento hexagonal fechado (hcp). Até certo ponto, metais amorfos e quasicristais também podem ser modelados por compactação de esferas. A ordem atômica local é bem modelada por um empacotamento compacto de tetraedros, levando a uma ordem icosaédrica imperfeita.

Um tetraedro regular é a configuração mais densa para o empacotamento de quatro esferas iguais. O problema de empacotamento aleatório denso de esferas duras pode então ser mapeado no problema de empacotamento tetraédrico . É um exercício prático tentar embalar bolas de tênis de mesa para formar apenas configurações tetraédricas. Um começa com quatro bolas dispostas como um tetraedro perfeito e tenta adicionar novas esferas, enquanto forma novos tetraedros. A próxima solução, com cinco bolas, é trivialmente dois tetraedros compartilhando uma face comum; note que já com esta solução, a estrutura fcc, que contém orifícios tetraédricos individuais, não mostra tal configuração (os tetraedros compartilham arestas, não faces). Com seis bolas, três tetraedros regulares são construídos, e o cluster é incompatível com todas as estruturas cristalinas compactas (fcc e hcp). Adicionar uma sétima esfera dá um novo agrupamento consistindo em duas bolas "axiais" tocando uma a outra e cinco outras tocando as duas últimas bolas, a forma externa sendo uma bi-pirâmide pentagonal quase regular. No entanto, estamos enfrentando agora um problema real de empacotamento, análogo ao encontrado acima com os ladrilhos pentagonais em duas dimensões. O ângulo diedro de um tetraedro não é comensurável com 2 π ; conseqüentemente, um buraco permanece entre duas faces de tetraedros vizinhos. Como conseqüência, um mosaico perfeito do espaço euclidiano R ³ é impossível com tetraedros regulares. A frustração tem um caráter topológico: é impossível preencher o espaço euclidiano com tetraedros, mesmo severamente distorcidos, se impormos que um número constante de tetraedros (aqui cinco) compartilham uma borda comum.

O próximo passo é crucial: a busca de uma estrutura não frustrada, permitindo a curvatura do espaço , para que as configurações locais se propaguem de forma idêntica e sem defeitos por todo o espaço.

Empacotamento regular de tetraedros: o politopo {3,3,5}

600 células : politopo {3,3,5}

Pacote de vinte tetraedros irregulares com um vértice comum, de modo que os doze vértices externos formam um icosaedro regular. De fato, o comprimento da borda do icosaedro l é ligeiramente maior do que o raio da circunsfera r ( l  ≈ 1,05 r ). Existe uma solução com tetraedros regulares se o espaço não for euclidiano, mas esférico. É o politopo {3,3,5}, usando a notação de Schläfli , também conhecida como célula-600 .

Existem cento e vinte vértices, todos pertencentes à hiperesfera S ³ com raio igual à razão áurea ( φ  = 1 + √ 5/2) se as bordas tiverem comprimento unitário. As seiscentas células são tetraedros regulares agrupados por cinco em torno de uma borda comum e por vinte em torno de um vértice comum. Essa estrutura é chamada de politopo (ver Coxeter ), que é o nome geral em dimensões superiores na série que contém polígonos e poliedros. Mesmo que essa estrutura esteja embutida em quatro dimensões, ela foi considerada uma variedade tridimensional (curva). Este ponto é conceitualmente importante pelo seguinte motivo. Os modelos ideais que foram introduzidos no Espaço curvo são modelos curvos tridimensionais. Eles parecem localmente como modelos euclidianos tridimensionais. Assim, o {3,3,5} politopo, que é um mosaico por tetraedros, fornece uma estrutura atômica muito densa se os átomos estiverem localizados em seus vértices. É, portanto, naturalmente utilizado como gabarito para metais amorfos, mas não se deve esquecer que ao preço de idealizações sucessivas.

Literatura

• Sadoc, JF; Mosseri, R. (2007). Frustração geométrica (edição reeditada). Cambridge University Press. ISBN 9780521031875.
• Sadoc, JF, ed. (1990). Geometria em Física da Matéria Condensada . Singapura: World Scientific. ISBN 9789810200893.
• Coxeter, HSM (1973). Polytopes regulares . Dover Publishing. ISBN 9780486614809.

Referências