Equação do tempo - Equation of time
A equação do tempo descreve a discrepância entre dois tipos de tempo solar . A palavra equação é usada no sentido medieval de "reconciliar uma diferença". Os dois tempos que diferem são o tempo solar aparente , que rastreia diretamente o movimento diurno do Sol , e o tempo solar médio , que rastreia um Sol médio teórico com movimento uniforme ao longo do equador celestial. O tempo solar aparente pode ser obtido pela medição da posição atual ( ângulo horário ) do Sol, conforme indicado (com precisão limitada) por um relógio de sol . O tempo solar médio , para o mesmo lugar, seria o tempo indicado por um relógio fixo ajustado de forma que ao longo do ano suas diferenças em relação ao tempo solar aparente tivessem uma média zero.
A equação do tempo é o componente leste ou oeste do analema , uma curva que representa o deslocamento angular do Sol em relação à sua posição média na esfera celeste , vista da Terra. A equação dos valores de tempo para cada dia do ano, compilada por observatórios astronômicos , foi amplamente listada em almanaques e efemérides .
O conceito

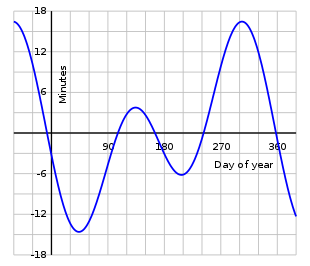
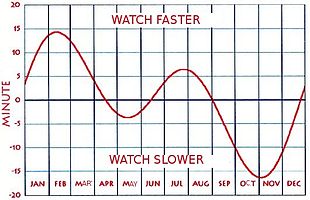
Durante um ano, a equação do tempo varia conforme mostrado no gráfico; sua mudança de um ano para o outro é pequena. O tempo aparente e o relógio de sol podem estar à frente (rápido) em até 16 min 33 s (por volta de 3 de novembro) ou atrasado (lento) em até 14 min 6 s (por volta de 11 de fevereiro). A equação do tempo tem zeros próximos a 15 de abril, 13 de junho, 1 de setembro e 25 de dezembro. Ignorando mudanças muito lentas na órbita e rotação da Terra, esses eventos se repetem na mesma época a cada ano tropical . No entanto, devido ao número não integral de dias em um ano, essas datas podem variar em um dia ou mais de ano para ano.
O gráfico da equação do tempo é aproximado pela soma de duas curvas senoidais, uma com período de um ano e outra com período de meio ano. As curvas refletem dois efeitos astronômicos, cada um causando uma não uniformidade diferente no movimento diário aparente do Sol em relação às estrelas:
- a obliquidade da eclíptica (o plano do movimento orbital anual da Terra em torno do Sol), que é inclinada em cerca de 23,44 graus em relação ao plano do equador da Terra ; e
- a excentricidade da órbita da Terra em torno do Sol, que é cerca de 0,0167.
A equação do tempo é constante apenas para um planeta com inclinação axial zero e excentricidade orbital zero . Em Marte, a diferença entre a hora do relógio de sol e a hora do relógio pode chegar a 50 minutos, devido à excentricidade consideravelmente maior de sua órbita. O planeta Urano , que tem uma inclinação axial extremamente grande, tem uma equação de tempo que faz seus dias começarem e terminarem várias horas antes ou depois, dependendo de onde está em sua órbita.
Sinal da equação do tempo
O Observatório Naval dos Estados Unidos afirma que "a Equação do Tempo é a diferença do tempo solar aparente menos o tempo solar médio ", ou seja, se o sol está à frente do relógio, o sinal é positivo, e se o relógio está à frente do sol, o sinal é negativo . A equação do tempo é mostrada no gráfico superior acima para um período de pouco mais de um ano. O gráfico inferior (que cobre exatamente um ano civil) tem os mesmos valores absolutos, mas o sinal é invertido, pois mostra a que distância o relógio está à frente do sol. As publicações podem usar qualquer um dos formatos - no mundo de língua inglesa, o uso anterior é o mais comum, mas nem sempre é seguido. Qualquer pessoa que fizer uso de uma tabela ou gráfico publicado deve primeiro verificar seu uso de sinal. Freqüentemente, há uma nota ou legenda que o explica. Caso contrário, o uso pode ser determinado sabendo-se que, durante os primeiros três meses de cada ano, o relógio está à frente do relógio de sol. O mnemônico "NYSS" (pronuncia-se "bom"), para "ano novo, relógio de sol lento", pode ser útil. Algumas tabelas publicadas evitam a ambigüidade não usando sinais, mas mostrando frases como "relógio de sol rápido" ou "relógio de sol lento".
Neste artigo, e em outros na Wikipedia em inglês, um valor positivo da equação do tempo implica que um relógio de sol está à frente de um relógio.
História
A frase "equação de tempo" é derivada do latim medieval aequātiō diērum , que significa "equação de dias" ou "diferença de dias". A palavra aequātiō (e equação do inglês médio ) foi usada na astronomia medieval para tabular a diferença entre um valor observado e o valor esperado (como na equação do centro, a equação dos equinócios, a equação do epiciclo). Gerald J. Toomer usa o termo medieval "equação" do latim aequātiō , para a diferença de Ptolomeu entre o tempo solar médio e o tempo solar aparente. A definição de Johannes Kepler da equação é "a diferença entre o número de graus e minutos da anomalia média e os graus e minutos da anomalia corrigida".
A diferença entre o tempo solar aparente e o tempo médio era reconhecida pelos astrônomos desde a antiguidade, mas antes da invenção de relógios mecânicos precisos em meados do século 17, os relógios de sol eram os únicos relógios confiáveis, e o tempo solar aparente era o padrão geralmente aceito. O tempo médio não substituiu o tempo aparente nos almanaques e efemérides nacionais até o início do século XIX.
Astronomia primitiva
O movimento diário irregular do Sol era conhecido dos babilônios.
Livro III de Ptolomeu 's Almagesto (2º século) está preocupado principalmente com o Sol de anomalia, e ele tabulados a equação do tempo em suas Tabelas Handy . Ptolomeu discute a correção necessária para converter a travessia do meridiano do Sol para significar o tempo solar e leva em consideração o movimento não uniforme do Sol ao longo da eclíptica e a correção do meridiano para a longitude eclíptica do Sol. Ele afirma que a correção máxima é 8+1 ⁄ 3 graus de tempo ou 5 ⁄ 9 de uma hora (Livro III, capítulo 9). No entanto, ele não considerou o efeito relevante para a maioria dos cálculos, uma vez que era insignificante para as luminárias de movimento lento e apenas o aplicou para a luminária de movimento mais rápido, a Lua.
Com base na discussão de Ptolomeu no Almagesto , os valores para a equação do tempo (árabe taʿdīl al-ayyām bi layālayhā ) eram padrão para as tabelas ( zij ) nas obras da astronomia islâmica medieval .
Período moderno inicial
Uma descrição do tempo aparente e médio foi dada por Nevil Maskelyne no Almanaque Náutico de 1767: "O tempo aparente é aquele deduzido imediatamente do Sol, seja da observação de sua passagem pelo meridiano, ou de sua observação de Ascensão ou Poente . Desta vez é diferente daquele mostrado por Relógios e Relógios bem regulados em Land, que é chamado de Tempo Equacionado ou Médio. " Ele prosseguiu dizendo que, no mar, o tempo aparente encontrado na observação do Sol deve ser corrigido pela equação do tempo, se o observador precisar do tempo médio.
A hora certa foi originalmente considerada como aquela mostrada por um relógio de sol. Quando bons relógios mecânicos foram introduzidos, eles concordaram com relógios de sol apenas cerca de quatro datas a cada ano, então a equação do tempo foi usada para "corrigir" suas leituras para obter a hora do relógio de sol. Alguns relógios, chamados de relógios de equação , incluíam um mecanismo interno para realizar essa "correção". Mais tarde, à medida que os relógios se tornaram os bons relógios dominantes, o tempo não corrigido, ou seja, o "tempo médio", tornou-se o padrão aceito. As leituras dos relógios de sol, quando eram usados, eram então, e muitas vezes ainda são, corrigidas com a equação do tempo, usada na direção inversa de antes, para obter a hora do relógio. Muitos relógios de sol, portanto, têm tabelas ou gráficos da equação do tempo gravados neles para permitir ao usuário fazer essa correção.
A equação do tempo foi usada historicamente para acertar relógios . Entre a invenção de relógios precisos em 1656 e o advento dos serviços comerciais de distribuição de horário por volta de 1900, havia três maneiras terrestres comuns de acertar os relógios. Em primeiro lugar, no caso incomum de ter um astrônomo presente, o trânsito do sol através do meridiano (o momento em que o sol passou por cima) foi anotado; o relógio foi então acertado para meio-dia e compensado pelo número de minutos dado pela equação de tempo para aquela data. Em segundo lugar, e muito mais comumente, um relógio de sol foi lido, uma tabela da equação do tempo (geralmente gravada no mostrador) foi consultada e o relógio ou relógio ajustado de acordo. Eles calcularam o tempo médio, embora local a um ponto de longitude . O terceiro método não utilizou a equação do tempo; em vez disso, usou observações estelares para fornecer o tempo sideral , explorando a relação entre o tempo sideral e o tempo solar médio .
As primeiras tabelas a fornecer a equação do tempo de uma maneira essencialmente correta foram publicadas em 1665 por Christiaan Huygens . Huygens, seguindo a tradição de Ptolomeu e dos astrônomos medievais em geral, definiu seus valores para a equação do tempo de modo a tornar todos os valores positivos ao longo do ano.
Outro conjunto de tabelas foi publicado em 1672-73 por John Flamsteed , que mais tarde se tornou o primeiro Astrônomo Real do novo Observatório Real de Greenwich . Estas parecem ter sido as primeiras tabelas essencialmente corretas que deram o significado de hoje do Tempo Médio (anteriormente, como observado acima, o sinal da equação era sempre positivo e era definido em zero quando a hora aparente do nascer do sol era mais cedo em relação ao relógio hora do nascer do sol). Flamsteed adotou a convenção de tabular e nomear a correção no sentido de que deveria ser aplicada ao tempo aparente para fornecer o tempo médio.
A equação do tempo, baseada corretamente nos dois componentes principais da irregularidade do movimento aparente do Sol, não foi geralmente adotada até depois das tabelas de Flamsteed de 1672-73, publicadas com a edição póstuma das obras de Jeremiah Horrocks .
Robert Hooke (1635-1703), que analisou matematicamente a junta universal , foi o primeiro a notar que a geometria e a descrição matemática da equação (não secular) do tempo e da junta universal eram idênticas, e propôs o uso de uma junta universal junta na construção de um "relógio de sol mecânico".
Séculos 18 e início de 19
As correções nas tabelas de Flamsteed de 1672-1673 e 1680 deram tempo médio calculado essencialmente de forma correta e sem necessidade de compensação adicional. Mas os valores numéricos nas tabelas da equação do tempo mudaram um pouco desde então, devido a três fatores:
- melhorias gerais na precisão que vieram de refinamentos nas técnicas de medição astronômica,
- mudanças intrínsecas lentas na equação do tempo, ocorrendo como resultado de pequenas mudanças de longo prazo na obliquidade e excentricidade da Terra (afetando, por exemplo, a distância e as datas do periélio ), e
- a inclusão de pequenas fontes de variação adicional no movimento aparente do Sol, desconhecidas no século 17, mas descobertas a partir do século 18, incluindo os efeitos da Lua, Vênus e Júpiter.

De 1767 a 1833, o British Nautical Almanac and Astronomical Ephemeris tabulou a equação do tempo no sentido de 'adicionar ou subtrair (conforme indicado) o número de minutos e segundos declarados para ou do tempo aparente para obter o tempo médio'. Os tempos no Almanaque estavam no tempo solar aparente, porque o tempo a bordo da nave era geralmente determinado pela observação do sol. Esta operação seria realizada no caso incomum em que o tempo solar médio de uma observação fosse necessário. Nas edições desde 1834, todos os tempos estavam em tempo solar médio, porque a essa altura o tempo a bordo do navio era cada vez mais determinado por cronômetros marítimos . Consequentemente, as instruções consistiam em adicionar ou subtrair (conforme as instruções) o número de minutos declarado para ou do tempo médio para obter o tempo aparente. Portanto, agora a adição correspondia à equação ser positiva e a subtração correspondia a ela ser negativa.
Como o movimento diário aparente do Sol é uma revolução por dia, ou seja, 360 ° a cada 24 horas, e o próprio Sol aparece como um disco de cerca de 0,5 ° no céu, relógios de sol simples podem ser lidos com uma precisão máxima de cerca de um minuto. Como a equação do tempo tem um intervalo de cerca de 33 minutos, a diferença entre a hora do relógio de sol e a hora do relógio não pode ser ignorada. Além da equação do tempo, também é necessário aplicar correções devido à distância do meridiano do fuso horário local e do horário de verão , se houver.
O pequeno aumento do dia solar médio devido à desaceleração da rotação da Terra, em cerca de 2 ms por dia por século, que atualmente se acumula até cerca de 1 segundo a cada ano, não é levado em consideração nas definições tradicionais da equação de tempo, pois é imperceptível no nível de precisão dos relógios de sol.
Principais componentes da equação
Excentricidade da órbita da Terra

A terra gira em torno do Sol. Visto da Terra, o Sol parece girar uma vez em torno da Terra através das estrelas de fundo em um ano. Se a Terra orbitasse o Sol com uma velocidade constante, em uma órbita circular em um plano perpendicular ao eixo da Terra, então o Sol culminaria todos os dias exatamente no mesmo horário, e seria um perfeito cronometrista (exceto pelo efeito muito pequeno da desaceleração da rotação da Terra). Mas a órbita da Terra é uma elipse não centrada no Sol, e sua velocidade varia entre 30,287 e 29,291 km / s, de acordo com as leis de Kepler do movimento planetário , e sua velocidade angular também varia, e assim o Sol parece se mover mais rápido (em relação às estrelas de fundo) no periélio (atualmente em torno de 3 de janeiro) e mais lento no afélio meio ano depois.
Nestes pontos extremos, este efeito varia o dia solar aparente em 7,9 s / dia a partir de sua média. Consequentemente, as menores diferenças diárias de velocidade em outros dias são cumulativas até esses pontos, refletindo como o planeta acelera e desacelera em relação à média. Como resultado, a excentricidade da órbita da Terra contribui com uma variação periódica que é (na aproximação de primeira ordem) uma onda senoidal com uma amplitude de 7,66 min e um período de um ano para a equação do tempo. Os pontos zero são atingidos no periélio (início de janeiro) e afélio (início de julho); os valores extremos são no início de abril (negativo) e início de outubro (positivo).
Obliquidade da eclíptica
Mesmo se a órbita da Terra fosse circular, o movimento percebido do Sol ao longo de nosso equador celestial ainda não seria uniforme. Isso é uma consequência da inclinação do eixo de rotação da Terra em relação ao plano de sua órbita , ou equivalentemente, a inclinação da eclíptica (o caminho que o Sol parece tomar na esfera celestial ) em relação ao equador celestial . A projeção desse movimento em nosso equador celestial , ao longo do qual o "tempo do relógio" é medido, é máxima nos solstícios , quando o movimento anual do Sol é paralelo ao equador (causando amplificação da velocidade percebida) e produz principalmente uma mudança em ascensão reta . É um mínimo nos equinócios , quando o movimento aparente do Sol é mais inclinado e produz mais mudanças na declinação , deixando menos para o componente em ascensão reta , que é o único componente que afeta a duração do dia solar. Uma ilustração prática da obliquidade é que o deslocamento diário da sombra projetada pelo Sol em um relógio de sol, mesmo no equador, é menor perto dos solstícios e maior perto dos equinócios. Se esse efeito operasse sozinho, os dias teriam até 24 horas e 20,3 segundos de duração (medidos do meio-dia ao meio-dia solar) perto dos solstícios, e até 20,3 segundos mais curtos do que 24 horas perto dos equinócios.
Na figura à direita, podemos ver a variação mensal da inclinação aparente do plano da eclíptica ao meio-dia solar vista da Terra. Essa variação se deve à aparente precessão da rotação da Terra ao longo do ano, vista do Sol ao meio-dia solar.
Em termos da equação do tempo, a inclinação da eclíptica resulta na contribuição de uma variação da onda senoidal com amplitude de 9,87 minutos e período de meio ano para a equação do tempo. Os pontos zero desta onda senoidal são alcançados nos equinócios e solstícios, enquanto os extremos são no início de fevereiro e agosto (negativo) e no início de maio e novembro (positivo).
Efeitos seculares
Os dois fatores mencionados acima têm diferentes comprimentos de onda, amplitudes e fases, portanto, sua contribuição combinada é uma onda irregular. Na época de 2000, estes são os valores (em minutos e segundos com datas UT ):
| Apontar | Valor | Encontro |
|---|---|---|
| mínimo | -14 min 15 s | 11 de fevereiro |
| zero | 0 min 0 s | 15 de abril |
| máximo | +3 min 41 s | 14 de maio |
| zero | 0 min 0 s | 13 de junho |
| mínimo | -6 min 30 s | 26 de julho |
| zero | 0 min 0 s | 1 de setembro |
| máximo | +16 min 25 s | 3 de novembro |
| zero | 0 min 0 s | 25 de dezembro |
- ET = aparente - média. Positivo significa: o Sol corre rápido e culmina mais cedo, ou o relógio de sol está à frente do tempo médio. Uma ligeira variação anual ocorre devido à presença de anos bissextos, reajustando-se a cada 4 anos. A forma exata da equação da curva do tempo e o analema associado mudam lentamente ao longo dos séculos, devido a variações seculares tanto na excentricidade quanto na obliquidade. Neste momento, ambos estão diminuindo lentamente, mas aumentam e diminuem ao longo de uma escala de tempo de centenas de milhares de anos.
Em escalas de tempo mais curtas (milhares de anos), as mudanças nas datas do equinócio e do periélio serão mais importantes. O primeiro é causado pela precessão e desloca o equinócio para trás em comparação com as estrelas. Mas pode ser ignorado na discussão atual, pois nosso calendário gregoriano é construído de forma a manter a data do equinócio vernal em 20 de março (pelo menos com precisão suficiente para nosso objetivo aqui). A mudança do periélio é para a frente, cerca de 1,7 dias a cada século. Em 1246 o periélio ocorreu em 22 de dezembro, o dia do solstício, então as duas ondas contribuintes tinham pontos zero comuns e a equação da curva de tempo era simétrica: em Algoritmos Astronômicos Meeus dá fevereiro e novembro extremos de 15 m 39 se maio e Julho de 4 m 58 s. Antes disso, o mínimo de fevereiro era maior do que o máximo de novembro, e o máximo de maio, maior do que o mínimo de julho. Na verdade, nos anos anteriores a 1900 (1901 AEC), o máximo de maio era maior do que o máximo de novembro. No ano 2000 (2001 aC), o máximo de maio foi +12 minutos e alguns segundos, enquanto o máximo de novembro foi pouco menos de 10 minutos. A mudança secular é evidente quando comparamos um gráfico atual da equação do tempo (veja abaixo) com um de 2.000 anos atrás, por exemplo, um construído a partir dos dados de Ptolomeu.
Representação gráfica

Uso pratico
Se o gnômon (o objeto que projeta a sombra) não for uma borda, mas um ponto (por exemplo, um buraco em uma placa), a sombra (ou ponto de luz) traçará uma curva ao longo do dia. Se a sombra for projetada em uma superfície plana, esta curva será uma seção cônica (geralmente uma hipérbole), uma vez que o círculo do movimento do Sol junto com o ponto do gnômon definem um cone. Nos equinócios de primavera e outono, o cone degenera em um plano e a hipérbole em uma linha. Com uma hipérbole diferente para cada dia, marcas de horas podem ser colocadas em cada hipérbole, incluindo as correções necessárias. Infelizmente, cada hipérbole corresponde a dois dias diferentes, um em cada semestre do ano, e esses dois dias exigirão correções diferentes. Um compromisso conveniente é traçar a linha para o "tempo médio" e adicionar uma curva mostrando a posição exata dos pontos de sombra ao meio-dia durante o ano. Essa curva terá a forma de um oito e é conhecida como analema . Comparando o analema com a linha média do meio-dia, a quantidade de correção a ser aplicada geralmente naquele dia pode ser determinada.
A equação do tempo é usada não apenas em relação a relógios de sol e dispositivos semelhantes, mas também para muitas aplicações de energia solar . Máquinas como rastreadores solares e heliostatos precisam se mover de maneira influenciada pela equação do tempo.
A hora civil é a hora média local para um meridiano que geralmente passa perto do centro do fuso horário e pode ser alterado posteriormente pelo horário de verão . Quando a hora solar aparente que corresponde a uma determinada hora civil for encontrada, a diferença de longitude entre o local de interesse e o meridiano do fuso horário, o horário de verão e a equação do tempo devem ser considerados.
Calculando a equação do tempo
A equação do tempo é obtida de uma tabela publicada ou gráfico. Para datas no passado, tais tabelas são produzidas a partir de medições históricas ou por cálculo; para datas futuras, é claro, as tabelas só podem ser calculadas. Em dispositivos como helióstatos controlados por computador, o computador é frequentemente programado para calcular a equação do tempo. O cálculo pode ser numérico ou analítico. Os primeiros são baseados na integração numérica das equações diferenciais do movimento, incluindo todos os efeitos gravitacionais e relativísticos significativos. Os resultados são precisos em mais de 1 segundo e são a base para dados de almanaque modernos. Os últimos são baseados em uma solução que inclui apenas a interação gravitacional entre o Sol e a Terra, mais simples, mas não tão precisa quanto a primeira. Sua precisão pode ser melhorada incluindo pequenas correções.
A discussão a seguir descreve um algoritmo razoavelmente preciso (concordando com os dados do almanaque dentro de 3 segundos ao longo de uma ampla gama de anos) para a equação do tempo que é bem conhecido dos astrônomos. Também mostra como obter uma fórmula aproximada simples (com precisão de 1 minuto em um grande intervalo de tempo), que pode ser facilmente avaliada com uma calculadora e fornece uma explicação simples do fenômeno que foi usado anteriormente neste artigo.
Descrição matemática
A definição precisa da equação do tempo é
- EOT = GHA - GMHA
As quantidades que ocorrem nesta equação são
- EOT, a diferença de tempo entre o tempo solar aparente e o tempo solar médio ;
- GHA, o ângulo da hora de Greenwich do Sol aparente (real);
- GMHA = Hora Universal - Offset, o Ângulo da Hora Média de Greenwich do Sol médio (fictício).
Aqui, o tempo e o ângulo são quantidades relacionadas por fatores como: 2 π radianos = 360 ° = 1 dia = 24 horas. A diferença, EOT, é mensurável, pois GHA é um ângulo que pode ser medido e o Tempo Universal , UT, é uma escala para a medição do tempo. O deslocamento de π = 180 ° = 12 horas de UT é necessário porque UT é zero na meia-noite média, enquanto GMHA = 0 no meio-dia médio. Tanto o GHA quanto o GMHA, como todos os ângulos físicos, têm uma descontinuidade matemática, mas não física, em seus respectivos (aparentes e médios) meio-dia. Apesar das descontinuidades matemáticas de seus componentes, a EOT é definida como uma função contínua pela adição (ou subtração) de 24 horas no pequeno intervalo de tempo entre as descontinuidades em GHA e GMHA.
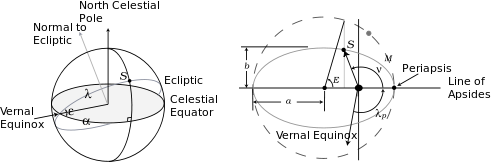
De acordo com as definições dos ângulos na esfera celeste GHA = GAST - α (ver ângulo horário )
onde:
- GAST é o tempo sideral aparente de Greenwich (o ângulo entre o equinócio vernal aparente e o meridiano no plano do equador). Esta é uma função conhecida do UT.
- α é a ascensão reta do Sol aparente (o ângulo entre o equinócio vernal aparente e o Sol real no plano do equador).
Ao substituir na equação do tempo, é
- EOT = GAST - α - UT + deslocamento
Como a fórmula para GHA acima, pode-se escrever GMHA = GAST - α M , onde o último termo é a ascensão reta do Sol médio. A equação é frequentemente escrita nestes termos como
- EOT = α M - α
onde α M = GAST - UT + offset . Nesta formulação, uma medição ou cálculo de EOT em um determinado valor de tempo depende de uma medição ou cálculo de α naquele momento. Tanto α quanto α M variam de 0 a 24 horas ao longo de um ano. O primeiro tem uma descontinuidade em um momento que depende do valor de UT, enquanto o último o tem em um momento um pouco posterior. Como consequência, quando calculado desta forma, EOT tem duas descontinuidades artificiais. Eles podem ambos ser removidos pela subtracção 24 horas a partir do valor de EOT no pequeno intervalo de tempo após a descontinuidade em α e antes daquele em α M . O EOT resultante é uma função contínua do tempo.
Outra definição, denotada por E para distingui-la de EOT, é
- E = GMST - α - UT + deslocamento
Aqui GMST = GAST - eqeq , é o tempo sideral médio de Greenwich (o ângulo entre o equinócio vernal médio e o Sol médio no plano do equador). Portanto, GMST é uma aproximação de GAST (e E é uma aproximação de EOT); eqeq é chamada de equação dos equinócios e é devido à oscilação ou nutação do eixo de rotação da Terra em torno de seu movimento de precessão. Uma vez que a amplitude do movimento nutacional é apenas cerca de 1,2 s (18 ″ de longitude), a diferença entre EOT e E pode ser ignorada, a menos que alguém esteja interessado na precisão de subsegundos.
Uma terceira definição, denotada Δ t para distingui-la de EOT e E , e agora chamada de Equação do Tempo das Efemérides (antes da distinção que agora é feita entre EOT, E e Δ t, a última era conhecida como a equação do tempo) é
- Δ t = Λ - α
aqui Λ é a longitude eclíptica do Sol médio (o ângulo do equinócio vernal médio ao Sol médio no plano da eclíptica ).
A diferença Λ - (GMST - UT + deslocamento) é de 1,3 s de 1960 a 2040. Portanto, ao longo deste intervalo restrito de anos Δ t é uma aproximação de EOT cujo erro está na faixa de 0,1 a 2,5 s dependendo da correção de longitude em a equação dos equinócios; para muitos propósitos, por exemplo, corrigir um relógio de sol, essa precisão é mais do que boa.
Cálculo de ascensão reta
A ascensão reta e, portanto, a equação do tempo, podem ser calculadas a partir da teoria do movimento celeste de dois corpos de Newton, na qual os corpos (Terra e Sol) descrevem órbitas elípticas em torno de seu centro de massa comum. Usando esta teoria, a equação do tempo torna-se
- Δ t = M + λ p - α
onde os novos ângulos que aparecem são
- M = 2π ( t - t p )/t S, é a anomalia média , o ângulo do periapsis da órbita elíptica ao Sol médio; seu intervalo é de 0 a 2 π conforme t aumenta de t p para t p + t Y ;
- t Y =365,259 6358 dias é o período de tempo em um ano anômalo : o intervalo de tempo entre duas passagens sucessivas do periapsia;
- λ p = Λ - M , é a longitude eclíptica do periapsia;
- t é o tempo dinâmico , a variável independente na teoria. Aqui é considerado idêntico ao tempo contínuo baseado em UT (veja acima), mas em cálculos mais precisos (de E ou EOT) a pequena diferença entre eles deve ser considerada, bem como a distinção entre UT1 e UTC.
- t p é o valor de t no periapsia.
Para completar o cálculo, três ângulos adicionais são necessários:
- E , a anomalia excêntrica do Sol(observe que isso é diferente de M );
- ν , a verdadeira anomalia do Sol;
- λ = ν + λ p , a verdadeira longitude do Sol na eclíptica.
Todos esses ângulos são mostrados na figura à direita, que mostra a esfera celeste e a órbita elíptica do Sol vista da Terra (a mesma que a órbita da Terra vista do Sol). Nesta figura ε é a obliquidade , enquanto e = √ 1 - ( b / a ) 2 é a excentricidade da elipse.
Agora, dado um valor de 0 ≤ M ≤ 2π , pode-se calcular α ( M ) por meio do seguinte procedimento bem conhecido:
Primeiro, dado M , calcule E a partir da equação de Kepler :
- M = E - e sen E
Embora esta equação não possa ser resolvida exatamente na forma fechada, os valores de E ( M ) podem ser obtidos a partir de séries infinitas (potência ou trigonométricas), métodos gráficos ou numéricos. Como alternativa, observe que para e = 0 , E = M e por iteração:
- E ≈ M + e pecado M .
Esta aproximação pode ser melhorada, para e pequeno , iterando novamente,
- E ≈ M + e sen M +1/2e 2 sen 2 M ,
e a iteração contínua produz termos de ordem sucessivamente mais altos da expansão da série de potências em e . Para valores pequenos de e (muito menos que 1), dois ou três termos da série fornecem uma boa aproximação para E ; quanto menor e , melhor é a aproximação.
Em seguida, sabendo E , calcule a anomalia verdadeira ν de uma relação de órbita elíptica
O ramo correto da função de múltiplos valores tan −1 x a usar é aquele que torna ν uma função contínua de E ( M ) começando de ν E = 0 = 0 . Assim, para 0 ≤ E <π use tan −1 x = Tan −1 x , e para π < E ≤ 2π use tan −1 x = Tan −1 x + π . No valor específico E = π para que o argumento de bronzeado é infinito, o uso ν = E . Aqui Tan −1 x é o ramo principal, | Tan −1 x | <π/2; a função que é retornada por calculadoras e aplicativos de computador. Alternativamente, esta função pode ser expressa em termos de sua série de Taylor em e , os três primeiros termos dos quais são:
- ν ≈ E + e sen E +1/4e 2 sin 2 E .
Para e pequeno, essa aproximação (ou mesmo apenas os dois primeiros termos) é boa. Combinar a aproximação para E ( M ) com esta para ν ( E ) produz
- ν ≈ M + 2 e sen M +5/4e 2 sin 2 M .
A relação ν ( M ) é chamada de equação do centro ; a expressão escrita aqui é uma aproximação de segunda ordem em e . Para o pequeno valor de e que caracteriza a órbita da Terra, isso dá uma boa aproximação para ν ( M ) .
Em seguida, sabendo ν , calcule λ a partir de sua definição:
- λ = ν + λ p
O valor de λ varia não linearmente com M porque a órbita é elíptica e não circular. Da aproximação para ν :
- λ ≈ M + λ p + 2 e sen M +5/4e 2 sin 2 M .
Finalmente, sabendo λ, calcule α a partir de uma relação para o triângulo retângulo na esfera celeste mostrada acima
- α = tan −1 (cos ε tan λ )
Observe que o quadrante de α é o mesmo de λ , portanto, reduza λ para o intervalo de 0 a 2 π e escreva
- α = Tan −1 (cos ε tan λ ) + k π ,
onde k é 0 se λ está no quadrante 1, é 1 se λ está nos quadrantes 2 ou 3 e é 2 se λ está no quadrante 4. Para os valores em que tan é infinito, α = λ .
Embora valores aproximados para α possam ser obtidos a partir de séries de Taylor truncadas como aquelas para ν , é mais eficaz usar a equação
- α = λ - sin −1 [ y sin ( α + λ )]
onde y = tan 2 (ε/2) . Observe que para ε = y = 0 , α = λ e iterando duas vezes:
- α ≈ λ - y sen 2 λ +1/2y 2 sen 4 λ .
Equação do tempo
A equação do tempo é obtida substituindo o resultado do cálculo da ascensão reta em uma fórmula da equação do tempo. Aqui Δ t ( M ) = M + λ p - α [ λ ( M )] é usado; em parte porque não estão incluídas pequenas correções (da ordem de 1 segundo), que justificariam o uso de E , e em parte porque o objetivo é obter uma expressão analítica simples. O uso de aproximações de dois termos para λ ( M ) e α ( λ ) permite que Δ t seja escrito como uma expressão explícita de dois termos, que é designada Δ t ey porque é uma aproximação de primeira ordem em e e em y .
- Δ t ey = −2 e sin M + y sin (2 M + 2 λ p ) = −7,659 sen M + 9,863 sin (2 M + 3,5932) minutos
Essa equação foi derivada pela primeira vez por Milne, que a escreveu em termos de λ = M + λ p . Os valores numéricos escritos aqui resultam do uso dos valores dos parâmetros orbitais, e =0,016 709 , ε =23,4393 ° =0,409 093 radianos, e λ p =282,9381 ° =4.938 201 radianos que correspondem à época de 1º de janeiro de 2000 às 12 horas UT1 . Ao avaliar a expressão numérica para Δ t ey conforme dado acima, uma calculadora deve estar no modo radianos para obter valores corretos porque o valor de 2 λ p - 2π no argumento do segundo termo está escrito em radianos. Aproximações de ordem superior também podem ser escritas, mas necessariamente têm mais termos. Por exemplo, a aproximação de segunda ordem em e e y consiste em cinco termos
- Δ t e 2 y 2 = Δ t ey -5/4e 2 sen 2 M + 4ey sen M cos (2 M + 2 λ p ) -1/2y 2 sin (4 M + 4 λ p )
Essa aproximação tem o potencial de alta precisão, no entanto, para alcançá-la em uma ampla faixa de anos, os parâmetros e , ε e λ p devem variar com o tempo. Isso cria complicações adicionais de cálculo. Outras aproximações foram propostas, por exemplo, Δ t e que usa a equação de primeira ordem do centro, mas nenhuma outra aproximação para determinar α , e Δ t e 2 que usa a equação de segunda ordem do centro.
A variável de tempo, M , pode ser escrita em termos de n , o número de dias após o periélio, ou D , o número de dias após uma data e hora específicas (época):
- M =2π/t Sn dias = M D +2π/t SD dias =6,240 040 77 +0,017 201 97 D
Aqui, M D é o valor de M na data e hora escolhidas. Para os valores dados aqui, em radianos, M D é o medido para o Sol real na época, 1 de janeiro de 2000 ao meio-dia UT1, e D é o número de dias após essa época. No periapsia M = 2π , então a resolução dá D = D p =2.508 109 . Isso coloca o periapsia em 4 de janeiro de 2000 às 00:11:41, enquanto o periapsia real é, de acordo com os resultados do Multiyear Interactive Computer Almanac (abreviado como MICA), em 3 de janeiro de 2000 às 05:17:30. Essa grande discrepância ocorre porque a diferença entre o raio orbital nas duas localizações é de apenas 1 parte em um milhão; em outras palavras, o raio é uma função muito fraca do tempo próximo ao periapsia. Na prática, isso significa que não se pode obter um resultado altamente preciso para a equação do tempo usando n e adicionando a data real do periapsia para um determinado ano. No entanto, de alta precisão pode ser conseguido através da utilização da formulação em termos de D .
Quando D > D p , M é maior que 2 π e deve-se subtrair um múltiplo de 2 π (que depende do ano) dele para colocá-lo no intervalo de 0 a 2 π . Da mesma forma, para anos anteriores a 2000, deve-se adicionar múltiplos de 2 π . Por exemplo, para o ano de 2010, D varia de3653 em 1 de janeiro ao meio-dia para4017 em 31 de dezembro ao meio-dia; os valores M correspondentes são69.078 9468 e75,340 4748 e são reduzidos ao intervalo de 0 a 2 π subtraindo 10 e 11 vezes 2 π, respectivamente. Sempre se pode escrever D = n Y + d , onde n Y é o número de dias desde a época até o meio-dia de 1º de janeiro do ano desejado e 0 ≤ d ≤ 364 (365 se o cálculo for para um ano bissexto).
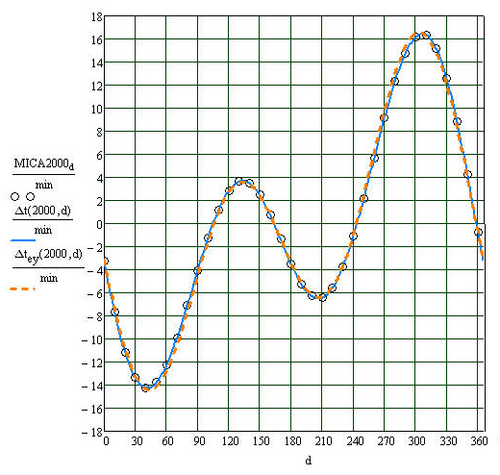
O resultado dos cálculos geralmente é dado como um conjunto de valores tabulares ou um gráfico da equação do tempo como uma função de d . Uma comparação dos gráficos de Δ t , Δ t ey e resultados do MICA para o ano 2000 é mostrada na figura à direita. O gráfico de Δ t ey é visto como próximo aos resultados produzidos por MICA, o erro absoluto, Err = | Δ t ey - MICA2000 | , é inferior a 1 minuto ao longo do ano; seu maior valor é 43,2 segundos e ocorre no dia 276 (3 de outubro). O gráfico de Δ t é indistinguível dos resultados do MICA, o maior erro absoluto entre os dois é de 2,46 s no dia 324 (20 de novembro).
Comentário sobre a continuidade da equação do tempo
Para a escolha do ramo apropriado da relação arctan com respeito à continuidade da função, uma versão modificada da função arco tangente é útil. Traz conhecimento prévio sobre o valor esperado por um parâmetro. A função arco tangente modificada é definida como:
- arctan η x = arctan x + π round (η - arctan x/π) .
Ele produz um valor que é o mais próximo possível de η . A função redondos rodadas para o número inteiro mais próximo.
Aplicando este rendimento:
- Δ t ( M ) = M + λ p - arctan ( M + λ p ) (cos ε tan λ ) .
O parâmetro M + λ p organiza aqui para definir Δ t para o valor zero mais próximo que é o desejado.
Efeitos seculares
A diferença entre os resultados do MICA e do Δ t foi verificada a cada 5 anos no intervalo de 1960 a 2040. Em todos os casos, o erro absoluto máximo foi inferior a 3 s; a maior diferença, 2,91 s, ocorreu em 22 de maio de 1965 (dia 141). No entanto, para atingir esse nível de precisão ao longo desse intervalo de anos, é necessário levar em consideração a mudança secular nos parâmetros orbitais com o tempo. As equações que descrevem essa variação são:
De acordo com essas relações, em 100 anos ( D = 36 525 ), λ p aumenta em cerca de 0,5% (1,7 °), e diminui em cerca de 0,25% e ε diminui em cerca de 0,05%.
Como resultado, o número de cálculos necessários para qualquer uma das aproximações de ordem superior da equação do tempo requer um computador para completá-los, se alguém deseja atingir sua precisão inerente em um amplo intervalo de tempo. Nesse caso, não é mais difícil avaliar Δ t usando um computador do que qualquer uma de suas aproximações.
Com tudo isso, observe que Δ t ey como escrito acima é fácil de avaliar, mesmo com uma calculadora, é preciso o suficiente (melhor do que 1 minuto no intervalo de 80 anos) para corrigir relógios de sol e tem uma bela explicação física como a soma de dois termos, um por obliquidade e outro por excentricidade que foi utilizado anteriormente no artigo. Isso não é verdade para Δ t considerado como uma função de M ou para qualquer uma de suas aproximações de ordem superior.
Cálculo alternativo
Outro procedimento para calcular a equação do tempo pode ser feito da seguinte maneira. Os ângulos estão em graus; aplica-se a ordem convencional de operações .
- n =360 °/365,24 dias,
onde n é a velocidade orbital angular média da Terra em graus por dia, também conhecida como "o movimento diário médio" .
- A = n × ( D + 9)
onde D é a data, contada em dias começando em 1 em 1 de janeiro (ou seja, a parte dos dias da data ordinal no ano). 9 é o número aproximado de dias do solstício de dezembro a 31 de dezembro. Um é o ângulo da Terra iria seguir em sua órbita em sua velocidade média do solstício de dezembro a data D .
- B = A +360 °/π× 0,0167 × sen [ n ( D - 3)]
B é o ângulo que a Terra se move do solstício até a data D , incluindo uma correção de primeira ordem para a excentricidade orbital da Terra, 0,0167. O número 3 é o número aproximado de dias de 31 de dezembro até a data atual do periélio da Terra . Esta expressão para B pode ser simplificada combinando constantes para:
- B = A + 1,914 ° × sen [ n ( D - 3)] .
Aqui, C é a diferença entre o ângulo movido na velocidade média e o ângulo na velocidade corrigida projetado no plano equatorial e dividido por 180 ° para obter a diferença em " meias voltas ". O valor 23,44 ° é a inclinação do eixo da Terra ("obliquidade") . A subtração dá o sinal convencional para a equação do tempo. Para qualquer dado valor de x , arctan x (às vezes escrito como tan −1 x ) tem vários valores, diferindo uns dos outros por números inteiros de meias voltas. O valor gerado por uma calculadora ou computador pode não ser o apropriado para este cálculo. Isso pode fazer com que C esteja errado por um número inteiro de meias voltas. As meias voltas em excesso são removidas na próxima etapa do cálculo para dar a equação do tempo:
- EOT = 720 × ( C - nint ( C )) minutos
A expressão nint ( C ) significa o número inteiro mais próximo para C . Em um computador, ele pode ser programado, por exemplo, como INT(C + 0.5). Seu valor é 0, 1 ou 2 em diferentes épocas do ano. Subtraindo-o deixa um pequeno número fracionário positivo ou negativo de meias voltas, que é multiplicado por 720, o número de minutos (12 horas) que a Terra leva para girar meia volta em relação ao Sol, para obter a equação do tempo.
Em comparação com os valores publicados, este cálculo tem uma raiz quadrada média do erro de apenas 3,7 s. O maior erro é 6,0 s. Isso é muito mais preciso do que a aproximação descrita acima, mas não tão preciso quanto o cálculo elaborado.
Adendo sobre declinação solar
O valor de B no cálculo acima é um valor preciso para a longitude eclíptica do Sol (deslocada em 90 °), então a declinação solar torna-se prontamente disponível:
- Declinação = −arcsin (sen 23,44 ° × cos B )
que tem uma precisão de uma fração de grau.
Veja também
Notas e notas de rodapé
- Notas
- Notas de rodapé
Referências
- Helyar, AG "Sun Data" . Arquivado do original em 11 de janeiro de 2004.
- Meeus, J (1997). Mathematical Astronomy Morsels . Richmond, Virginia: Willman-Bell.
- McCarthy, Dennis D .; Seidelmann, P. Kenneth (2009). TIME From Earth Rotation to Atomic Physics . Weinheim: Wiley VCH. ISBN 978-3-527-40780-4.
links externos
- NOAA Solar Calculator
- Serviços de dados USNO (incluem tempos de nascer / pôr / trânsito do Sol e outros objetos celestes)
- A equação do tempo descrito no Greenwich Observatory web site
- Um site analema com muitas ilustrações
- A Equação do Tempo e o Analemma , de Kieron Taylor
- Um artigo de Brian Tung contendo um link para um programa C usando uma fórmula mais precisa do que a maioria (especialmente em inclinações e excentricidades altas). O programa pode calcular a declinação solar, Equação do Tempo ou Analemma.
- Fazendo cálculos usando os modelos planetários geocêntricos de Ptolomeu com uma discussão de seu gráfico ET
- Equação de Tempo Longcase Clock de John Topping C.1720
- A equação da tabela de correção de tempo Uma página que descreve como corrigir um relógio para um relógio de sol.
- Tempômetro solar - Calcule seu tempo solar, incluindo a equação do tempo.