Correlação - Correlation

Vários conjuntos de ( x ,  y ) pontos, com o coeficiente de correlação de Pearson de x e y para cada conjunto. A correlação reflete o ruído e a direção de uma relação linear (linha superior), mas não a inclinação dessa relação (meio), nem muitos aspectos das relações não lineares (parte inferior). NB: a figura do centro tem uma inclinação de 0, mas nesse caso o coeficiente de correlação é indefinido porque a variância de Y é zero.

Em estatística , correlação ou dependência é qualquer relação estatística, causal ou não, entre duas variáveis ​​aleatórias ou dados bivariados . No sentido mais amplo, correlação é qualquer associação estatística, embora geralmente se refira ao grau em que um par de variáveis ​​está linearmente relacionado. Exemplos familiares de fenômenos dependentes incluem a correlação entre a altura dos pais e de seus filhos, e a correlação entre o preço de um bem e a quantidade que os consumidores estão dispostos a comprar, como é representado na chamada curva de demanda .

As correlações são úteis porque podem indicar uma relação preditiva que pode ser explorada na prática. Por exemplo, uma concessionária de eletricidade pode produzir menos energia em um dia ameno com base na correlação entre a demanda de eletricidade e o clima. Neste exemplo, há uma relação causal , porque o clima extremo faz com que as pessoas usem mais eletricidade para aquecimento ou resfriamento. No entanto, em geral, a presença de uma correlação não é suficiente para inferir a presença de uma relação causal (ou seja, correlação não implica causalidade ).

Formalmente, as variáveis ​​aleatórias são dependentes se não satisfizerem uma propriedade matemática de independência probabilística . Em linguagem informal, correlação é sinônimo de dependência . No entanto, quando usada em um sentido técnico, a correlação se refere a qualquer um dos vários tipos específicos de operações matemáticas entre as variáveis ​​testadas e seus respectivos valores esperados . Essencialmente, a correlação é a medida de como duas ou mais variáveis ​​estão relacionadas entre si. Existem vários coeficientes de correlação , frequentemente denotados ou , medindo o grau de correlação. O mais comum deles é o coeficiente de correlação de Pearson , que é sensível apenas a uma relação linear entre duas variáveis ​​(que pode estar presente mesmo quando uma variável é uma função não linear da outra). Outros coeficientes de correlação - como a correlação de classificação de Spearman - foram desenvolvidos para serem mais robustos do que os de Pearson, ou seja, mais sensíveis a relacionamentos não lineares. A informação mútua também pode ser aplicada para medir a dependência entre duas variáveis. ${\displaystyle \rho }$${\displaystyle r}$

Coeficiente de momento-produto de Pearson

Exemplos de gráficos de dispersão de vários conjuntos de dados com vários coeficientes de correlação.

Definição

A medida mais familiar de dependência entre duas grandezas é o coeficiente de correlação momento-produto de Pearson (PPMCC), ou "coeficiente de correlação de Pearson", comumente chamado simplesmente de "coeficiente de correlação". Matematicamente, é definido como a qualidade dos mínimos quadrados que se ajustam aos dados originais. É obtido tomando a razão da covariância das duas variáveis ​​em questão de nosso conjunto de dados numéricos, normalizada para a raiz quadrada de suas variâncias. Matematicamente, simplesmente divide-se a covariância das duas variáveis ​​pelo produto de seus desvios-padrão . Karl Pearson desenvolveu o coeficiente a partir de uma ideia semelhante, mas ligeiramente diferente, de Francis Galton .

Um coeficiente de correlação produto-momento de Pearson tenta estabelecer uma linha de melhor ajuste por meio de um conjunto de dados de duas variáveis, essencialmente estabelecendo os valores esperados e o coeficiente de correlação de Pearson resultante indica a que distância o conjunto de dados real está dos valores esperados. Dependendo do sinal do nosso coeficiente de correlação de Pearson, podemos terminar com uma correlação negativa ou positiva se houver qualquer tipo de relacionamento entre as variáveis ​​do nosso conjunto de dados.

O coeficiente de correlação população entre duas variáveis aleatórias e com os valores esperados e e desvios padrão e é definida como ${\displaystyle \rho _{X,Y}}$ ${\displaystyle X}$${\displaystyle Y}$ ${\displaystyle \mu _{X}}$${\displaystyle \mu _{Y}}$ ${\displaystyle \sigma _{X}}$${\displaystyle \sigma _{Y}}$

onde é o operador de valor esperado , significa covariância e é uma notação alternativa amplamente usada para o coeficiente de correlação. A correlação de Pearson é definida apenas se ambos os desvios padrão forem finitos e positivos. Uma fórmula alternativa puramente em termos de momentos é ${\displaystyle \operatorname {E} }$${\displaystyle \operatorname {cov} }$${\displaystyle \operatorname {corr} }$

Propriedade de simetria

O coeficiente de correlação é simétrica: . Isso é verificado pela propriedade comutativa da multiplicação. ${\displaystyle \operatorname {corr} (X,Y)=\operatorname {corr} (Y,X)}$

Correlação como produto

Deixe variáveis ​​aleatórias e tenham desvios padrão e . Então${\displaystyle X}$${\displaystyle Y}$ ${\displaystyle \sigma _{X}>0}$${\displaystyle \sigma _{Y}>0}$

Correlação e independência

É um corolário da desigualdade de Cauchy-Schwarz que o valor absoluto do coeficiente de correlação de Pearson não seja maior que 1. Portanto, o valor de um coeficiente de correlação varia entre -1 e +1. O coeficiente de correlação é um no caso de um perfeito directa (aumento) a relação linear (correlação), -1 no caso de um perfeito inversa (diminuir) a relação linear ( anti-correlao ), e algum valor no intervalo aberto em todos os outros casos, indicando o grau de dependência linear entre as variáveis. À medida que se aproxima de zero, há menos relacionamento (mais próximo de não correlacionado). Quanto mais próximo o coeficiente estiver de -1 ou 1, mais forte será a correlação entre as variáveis. ${\displaystyle (-1,1)}$

Se as variáveis ​​são independentes , o coeficiente de correlação de Pearson é 0, mas o inverso não é verdadeiro porque o coeficiente de correlação detecta apenas dependências lineares entre duas variáveis.

Por exemplo, suponha que a variável aleatória seja simetricamente distribuída em torno de zero, e . Então é completamente determinado por , de modo que e são perfeitamente dependentes, mas sua correlação é zero; eles não estão correlacionados . No entanto, no caso especial em que e são conjuntamente normais , a falta de correlação é equivalente à independência. ${\displaystyle X}$${\displaystyle Y=X^{2}}$${\displaystyle Y}$${\displaystyle X}$${\displaystyle X}$${\displaystyle Y}$${\displaystyle X}$${\displaystyle Y}$

Mesmo que os dados não correlacionados não impliquem necessariamente em independência, pode-se verificar se as variáveis ​​aleatórias são independentes se sua informação mútua for 0.

Coeficiente de correlação de amostra

Dada uma série de medidas do par indexado por , o coeficiente de correlação da amostra pode ser usado para estimar a correlação de Pearson da população entre e . O coeficiente de correlação da amostra é definido como ${\displaystyle n}$${\displaystyle (X_{i},Y_{i})}$${\displaystyle i=1,\ldots ,n}$${\displaystyle \rho _{X,Y}}$${\displaystyle X}$${\displaystyle Y}$

${\displaystyle r_{xy}\quad {\overset {\underset {\mathrm {def} }{}}{=}}\quad {\frac {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{(n-1)s_{x}s_{y}}}={\frac {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{\sqrt {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})^{2}\sum \limits _{i=1}^{n}(y_{i}-{\bar {y}})^{2}}}},}$

onde e são as médias da amostra de e , e e são os desvios padrão da amostra corrigida de e . ${\displaystyle {\overline {x}}}$${\displaystyle {\overline {y}}}$${\displaystyle X}$${\displaystyle Y}$${\displaystyle s_{x}}$${\displaystyle s_{y}}$${\displaystyle X}$${\displaystyle Y}$

Expressões equivalentes para são ${\displaystyle r_{xy}}$

${\displaystyle {\begin{aligned}r_{xy}&={\frac {\sum x_{i}y_{i}-n{\bar {x}}{\bar {y}}}{ns'_{x}s'_{y}}}\\[5pt]&={\frac {n\sum x_{i}y_{i}-\sum x_{i}\sum y_{i}}{{\sqrt {n\sum x_{i}^{2}-(\sum x_{i})^{2}}}~{\sqrt {n\sum y_{i}^{2}-(\sum y_{i})^{2}}}}}.\end{aligned}}}$

onde e são os desvios padrão da amostra não corrigida de e . ${\displaystyle s'_{x}}$${\displaystyle s'_{y}}$${\displaystyle X}$${\displaystyle Y}$

Se e forem resultados de medições que contêm erro de medição, os limites realistas do coeficiente de correlação não são -1 a +1, mas um intervalo menor. Para o caso de um modelo linear com uma única variável independente, o coeficiente de determinação (R ​​ao quadrado) é o quadrado do coeficiente momento-produto de Pearson. ${\displaystyle x}$${\displaystyle y}$${\displaystyle r_{xy}}$

Exemplo

Considere a distribuição de probabilidade conjunta de e fornecida na tabela abaixo. ${\displaystyle X}$${\displaystyle Y}$

${\displaystyle \operatorname {P} (X=x,Y=y)}$	${\displaystyle y=-1}$	${\displaystyle y=0}$	${\displaystyle y=1}$
${\displaystyle x=0}$	${\displaystyle 0}$	${\displaystyle 1/3}$	${\displaystyle 0}$
${\displaystyle x=1}$	${\displaystyle 1/3}$	${\displaystyle 0}$	${\displaystyle 1/3}$

Para esta distribuição conjunta, as distribuições marginais são:

${\displaystyle \operatorname {P} (X=x)={\begin{cases}1/3&\quad {\text{for }}x=0\\2/3&\quad {\text{for }}x=1\end{cases}}}$

${\displaystyle \operatorname {P} (Y=y)={\begin{cases}1/3&\quad {\text{for }}y=-1\\1/3&\quad {\text{for }}y=0\\1/3&\quad {\text{for }}y=1\end{cases}}}$

Isso produz as seguintes expectativas e variações:

${\displaystyle \mu _{X}=2/3}$

${\displaystyle \mu _{Y}=0}$

${\displaystyle \sigma _{X}^{2}=2/9}$

${\displaystyle \sigma _{Y}^{2}=2/3}$

Portanto:

${\displaystyle {\begin{aligned}\rho _{X,Y}&={\frac {1}{\sigma _{X}\sigma _{Y}}}\operatorname {E} [(X-\mu _{X})(Y-\mu _{Y})]\\[5pt]&={\frac {1}{\sigma _{X}\sigma _{Y}}}\sum _{x,y}{(x-\mu _{X})(y-\mu _{Y})\operatorname {P} (X=x,Y=y)}\\[5pt]&=(1-2/3)(-1-0){\frac {1}{3}}+(0-2/3)(0-0){\frac {1}{3}}+(1-2/3)(1-0){\frac {1}{3}}=0.\end{aligned}}}$

Coeficientes de correlação de classificação

Os coeficientes de correlação de classificação , como o coeficiente de correlação de classificação de Spearman e o coeficiente de correlação de classificação de Kendall (τ) medem até que ponto, conforme uma variável aumenta, a outra variável tende a aumentar, sem exigir que esse aumento seja representado por uma relação linear. Se, à medida que uma variável aumenta, a outra diminui , os coeficientes de correlação de classificação serão negativos. É comum considerar esses coeficientes de correlação de classificação como alternativas ao coeficiente de Pearson, usado para reduzir a quantidade de cálculo ou para tornar o coeficiente menos sensível à não normalidade nas distribuições. No entanto, essa visão tem pouca base matemática, pois os coeficientes de correlação de classificação medem um tipo diferente de relação do que o coeficiente de correlação produto-momento de Pearson e são mais vistos como medidas de um tipo diferente de associação, em vez de uma medida alternativa da população coeficiente de correlação.

Para ilustrar a natureza da correlação de classificação e sua diferença da correlação linear, considere os quatro pares de números a seguir : ${\displaystyle (x,y)}$

(0, 1), (10, 100), (101, 500), (102, 2000).

À medida que passamos de cada par para o próximo, o par aumenta, e o mesmo acontece . Essa relação é perfeita, no sentido de que um aumento em é sempre acompanhado por um aumento em . Isso significa que temos uma correlação de classificação perfeita e os coeficientes de correlação de Spearman e Kendall são 1, enquanto neste exemplo o coeficiente de correlação produto-momento de Pearson é 0,7544, indicando que os pontos estão longe de estar em uma linha reta. Da mesma forma, se sempre diminui quando aumenta , os coeficientes de correlação de classificação serão -1, enquanto o coeficiente de correlação produto-momento de Pearson pode ou não estar próximo de -1, dependendo de quão próximos os pontos estão de uma linha reta. Embora nos casos extremos de correlação de classificação perfeita os dois coeficientes sejam iguais (sendo ambos +1 ou -1), esse não é geralmente o caso e, portanto, os valores dos dois coeficientes não podem ser comparados de forma significativa. Por exemplo, para os três pares (1, 1) (2, 3) (3, 2) o coeficiente de Spearman é 1/2, enquanto o coeficiente de Kendall é 1/3. ${\displaystyle x}$${\displaystyle y}$${\displaystyle x}$${\displaystyle y}$${\displaystyle y}$${\displaystyle x}$

Outras medidas de dependência entre variáveis ​​aleatórias

A informação fornecida por um coeficiente de correlação não é suficiente para definir a estrutura de dependência entre variáveis ​​aleatórias. O coeficiente de correlação define completamente a estrutura de dependência apenas em casos muito particulares, por exemplo, quando a distribuição é uma distribuição normal multivariada . (Veja o diagrama acima.) No caso de distribuições elípticas, ele caracteriza as (hiper) elipses de igual densidade; entretanto, não caracteriza completamente a estrutura de dependência (por exemplo, os graus de liberdade de uma distribuição t multivariada determinam o nível de dependência da cauda).

A correlação de distância foi introduzida para abordar a deficiência da correlação de Pearson de que pode ser zero para variáveis ​​aleatórias dependentes; correlação de distância zero implica independência.

O coeficiente de dependência aleatória é uma medida de dependência computacionalmente eficiente, baseada em cópula , entre variáveis ​​aleatórias multivariadas. O RDC é invariável em relação a escalas não lineares de variáveis ​​aleatórias, é capaz de descobrir uma ampla gama de padrões de associação funcional e assume valor zero na independência.

Por duas variáveis binárias, o odds ratio mede sua dependência, e leva os números não negativos alcance, possivelmente infinito: . Estatísticas relacionados, tais como de Yule Y e do Yule Q normalizar este para a correlação do tipo gama . O odds ratio é generalizado pelo modelo logístico para modelar casos em que as variáveis ​​dependentes são discretas e pode haver uma ou mais variáveis ​​independentes. ${\displaystyle [0,+\infty ]}$${\displaystyle [-1,1]}$

O coeficiente de correlação , entropia baseados em informação mútua , de correlação total , de correlação total dupla e correlação policóricas são também capazes de detectar dependências mais gerais, como é a consideração da cópula entre elas, enquanto o coeficiente de determinação generaliza o coeficiente de correlação de regressão múltipla .

Sensibilidade à distribuição de dados

O grau de dependência entre as variáveis e não depende da escala em que as variáveis ​​são expressas. Ou seja, se estivermos analisando a relação entre e , a maioria das medidas de correlação não são afetadas pela transformação em a  +  bX e em c  +  dY , onde a , b , c e d são constantes ( b e d sendo positivos). Isso é verdade para algumas estatísticas de correlação, bem como para seus análogos populacionais. Algumas estatísticas de correlação, como o coeficiente de correlação de classificação, também são invariantes às transformações monótonas das distribuições marginais de e / ou . ${\displaystyle X}$${\displaystyle Y}$${\displaystyle X}$${\displaystyle Y}$${\displaystyle X}$${\displaystyle Y}$${\displaystyle X}$${\displaystyle Y}$

Os coeficientes de correlação de Pearson / Spearman entre e são mostrados quando os intervalos das duas variáveis ​​são irrestritos e quando o intervalo de é restrito ao intervalo (0,1).${\displaystyle X}$${\displaystyle Y}$${\displaystyle X}$

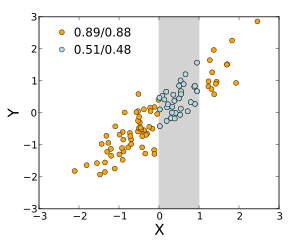
A maioria das medidas de correlação são sensíveis à maneira como e são amostradas. As dependências tendem a ser mais fortes se vistas em uma faixa mais ampla de valores. Assim, se considerarmos o coeficiente de correlação entre as alturas dos pais e seus filhos sobre todos os homens adultos, e compará-lo com o mesmo coeficiente de correlação calculado quando os pais são selecionados para ter entre 165 cm e 170 cm de altura, a correlação será mais fraco no último caso. Várias técnicas foram desenvolvidas para tentar corrigir a restrição de intervalo em uma ou ambas as variáveis ​​e são comumente usadas em meta-análises; as mais comuns são as equações do caso II e do caso III de Thorndike. ${\displaystyle X}$${\displaystyle Y}$

Várias medidas de correlação em uso pode ser indefinido para determinadas distribuições de conjuntos de X e Y . Por exemplo, o coeficiente de correlação de Pearson é definido em termos de momentos e, portanto, será indefinido se os momentos forem indefinidos. Medidas de dependência baseadas em quantis são sempre definidas. Estatísticas baseadas em amostra destinadas a estimar as medidas de dependência da população podem ou não ter propriedades estatísticas desejáveis, como ser imparcial ou assintoticamente consistente , com base na estrutura espacial da população da qual os dados foram amostrados.

A sensibilidade à distribuição de dados pode ser uma vantagem. Por exemplo, a correlação em escala é projetada para usar a sensibilidade ao intervalo a fim de selecionar correlações entre componentes rápidos de séries temporais. Ao reduzir a faixa de valores de maneira controlada, as correlações em escalas de tempo longas são filtradas e apenas as correlações em escalas de tempo curtas são reveladas.

Matrizes de correlação

A matriz de correlação de variáveis ​​aleatórias é a matriz cuja entrada é . Assim as diagonais são todos de forma idêntica unidade . Se as medidas de correlação usadas são coeficientes produto-momento, a matriz de correlação é a mesma que a matriz de covariância das variáveis ​​aleatórias padronizadas para . Isso se aplica tanto à matriz de correlações da população (nesse caso, o desvio padrão da população), quanto à matriz de correlações da amostra (em cujo caso denota o desvio padrão da amostra). Conseqüentemente, cada um é necessariamente uma matriz semidefinida positiva . Além disso, a matriz de correlação é definida estritamente positiva se nenhuma variável pode ter todos os seus valores gerados exatamente como uma função linear dos valores das outras. ${\displaystyle n}$${\displaystyle X_{1},\ldots ,X_{n}}$${\displaystyle n\times n}$${\displaystyle (i,j)}$${\displaystyle \operatorname {corr} (X_{i},X_{j})}$ ${\displaystyle X_{i}/\sigma (X_{i})}$${\displaystyle i=1,\dots ,n}$${\displaystyle \sigma }$${\displaystyle \sigma }$

A matriz de correlação é simétrica porque a correlação entre e é igual à correlação entre e . ${\displaystyle X_{i}}$${\displaystyle X_{j}}$${\displaystyle X_{j}}$${\displaystyle X_{i}}$

Uma matriz de correlação aparece, por exemplo, em uma fórmula para o coeficiente de determinação múltipla , uma medida de qualidade de ajuste em regressão múltipla .

Na modelagem estatística , as matrizes de correlação que representam as relações entre as variáveis ​​são categorizadas em diferentes estruturas de correlação, que são diferenciadas por fatores como o número de parâmetros necessários para estimá-las. Por exemplo, em uma matriz de correlação trocável , todos os pares de variáveis ​​são modelados como tendo a mesma correlação, então todos os elementos não diagonais da matriz são iguais uns aos outros. Por outro lado, uma matriz autorregressiva é freqüentemente usada quando as variáveis ​​representam uma série de tempo, uma vez que as correlações tendem a ser maiores quando as medidas estão mais próximas no tempo. Outros exemplos incluem independente, não estruturado, dependente de M e Toeplitz.

Na análise exploratória de dados , a iconografia das correlações consiste em substituir uma matriz de correlação por um diagrama onde as correlações “marcantes” são representadas por uma linha contínua (correlação positiva), ou uma linha pontilhada (correlação negativa).

Matriz de correlação válida mais próxima

Em algumas aplicações (por exemplo, construir modelos de dados a partir de dados apenas parcialmente observados), deseja-se encontrar a matriz de correlação "mais próxima" de uma matriz de correlação "aproximada" (por exemplo, uma matriz que normalmente carece de positividade semi-definida devido à forma como tem foi calculado).

Em 2002, Higham formalizou a noção de proximidade usando a norma Frobenius e forneceu um método para calcular a matriz de correlação mais próxima usando o algoritmo de projeção de Dykstra , do qual uma implementação está disponível como uma API da Web online.

Isso despertou interesse no assunto, com novos resultados teóricos (por exemplo, calcular a matriz de correlação mais próxima com a estrutura de fator) e numéricos (por exemplo, usar o método de Newton para calcular a matriz de correlação mais próxima) obtidos nos anos subsequentes.

Incorrelação e independência de processos estocásticos

Da mesma forma para dois processos estocásticos e : Se forem independentes, não estão correlacionados. O oposto desta afirmação pode não ser verdade. Mesmo se duas variáveis ​​não estiverem correlacionadas, elas podem não ser independentes uma da outra. ${\displaystyle \left\{X_{t}\right\}_{t\in {\mathcal {T}}}}$${\displaystyle \left\{Y_{t}\right\}_{t\in {\mathcal {T}}}}$

Equívocos comuns

Correlação e causalidade

O ditado convencional de que " correlação não implica causalidade " significa que a correlação não pode ser usada por si mesma para inferir uma relação causal entre as variáveis. Este dito não deve ser entendido como significando que as correlações não podem indicar a existência potencial de relações causais. No entanto, as causas subjacentes à correlação, se houver, podem ser indiretas e desconhecidas, e altas correlações também se sobrepõem às relações de identidade ( tautologias ), onde não existe processo causal. Consequentemente, uma correlação entre duas variáveis ​​não é uma condição suficiente para estabelecer uma relação causal (em qualquer direção).

Uma correlação entre idade e altura em crianças é causalmente transparente, mas uma correlação entre humor e saúde em pessoas é menos transparente. A melhora do humor leva à melhora da saúde, ou a boa saúde leva ao bom humor, ou ambos? Ou algum outro fator está por trás de ambos? Em outras palavras, uma correlação pode ser tomada como evidência de uma possível relação causal, mas não pode indicar qual poderia ser a relação causal, se houver.

Correlações lineares simples

Quatro conjuntos de dados com a mesma correlação de 0,816

O coeficiente de correlação de Pearson indica a força de uma relação linear entre duas variáveis, mas seu valor geralmente não caracteriza completamente sua relação. Em particular, se a média condicional de dado , denotado , não for linear em , o coeficiente de correlação não determinará totalmente a forma de . ${\displaystyle Y}$${\displaystyle X}$${\displaystyle \operatorname {E} (Y\mid X)}$${\displaystyle X}$${\displaystyle \operatorname {E} (Y\mid X)}$

A imagem adjacente mostra gráficos de dispersão do quarteto de Anscombe , um conjunto de quatro pares diferentes de variáveis ​​criado por Francis Anscombe . As quatro variáveis ​​possuem a mesma média (7,5), variância (4,12), correlação (0,816) e reta de regressão ( y  = 3 + 0,5 x ). No entanto, como pode ser visto nos gráficos, a distribuição das variáveis ​​é muito diferente. O primeiro (canto superior esquerdo) parece ter distribuição normal, e corresponde ao que se esperaria ao considerar duas variáveis ​​correlacionadas e seguindo o pressuposto de normalidade. O segundo (canto superior direito) não é distribuído normalmente; embora uma relação óbvia entre as duas variáveis ​​possa ser observada, ela não é linear. Nesse caso, o coeficiente de correlação de Pearson não indica que existe uma relação funcional exata: apenas a extensão em que essa relação pode ser aproximada por uma relação linear. No terceiro caso (canto inferior esquerdo), a relação linear é perfeita, exceto para um outlier que exerce influência suficiente para diminuir o coeficiente de correlação de 1 para 0,816. Por fim, o quarto exemplo (canto inferior direito) mostra outro exemplo em que um valor discrepante é suficiente para produzir um alto coeficiente de correlação, embora a relação entre as duas variáveis ​​não seja linear. ${\displaystyle y}$

Esses exemplos indicam que o coeficiente de correlação, como uma estatística de resumo, não pode substituir o exame visual dos dados. Às vezes, diz-se que os exemplos demonstram que a correlação de Pearson pressupõe que os dados seguem uma distribuição normal , mas isso é apenas parcialmente correto. A correlação de Pearson pode ser calculada com precisão para qualquer distribuição que tenha uma matriz de covariância finita , que inclui a maioria das distribuições encontradas na prática. No entanto, o coeficiente de correlação de Pearson (em conjunto com a média e a variância da amostra) é apenas uma estatística suficiente se os dados forem extraídos de uma distribuição normal multivariada . Como resultado, o coeficiente de correlação de Pearson caracteriza totalmente a relação entre as variáveis ​​se e somente se os dados forem extraídos de uma distribuição normal multivariada.

Distribuição normal bivariada

Se um par de variáveis ​​aleatórias segue uma distribuição normal bivariada , a média condicional é uma função linear de , e a média condicional é uma função linear de . O coeficiente de correlação entre e , junto com as médias marginais e variâncias de e , determina esta relação linear: ${\displaystyle (X,Y)}$${\displaystyle \operatorname {E} (X\mid Y)}$${\displaystyle Y}$${\displaystyle \operatorname {E} (Y\mid X)}$${\displaystyle X}$${\displaystyle \rho _{X,Y}}$${\displaystyle X}$${\displaystyle Y}$${\displaystyle X}$${\displaystyle Y}$

${\displaystyle \operatorname {E} (Y\mid X)=\operatorname {E} (Y)+\rho _{X,Y}\cdot \sigma _{Y}{\frac {X-\operatorname {E} (X)}{\sigma _{X}}},}$

onde e são os valores esperados de e , respectivamente, e e são os desvios padrão de e , respectivamente. ${\displaystyle \operatorname {E} (X)}$${\displaystyle \operatorname {E} (Y)}$${\displaystyle X}$${\displaystyle Y}$${\displaystyle \sigma _{X}}$${\displaystyle \sigma _{Y}}$${\displaystyle X}$${\displaystyle Y}$

Erro padrão

Se e são variáveis ​​aleatórias, um erro padrão é associado à correlação que é: ${\displaystyle x}$${\displaystyle y}$

${\displaystyle SE_{r}={\frac {1-r^{2}}{\sqrt {(n-2)}}}}$

onde está a correlação e o número de amostras. ${\displaystyle r}$${\displaystyle n}$

Veja também

Referências

Leitura adicional

• Cohen, J .; Cohen P .; West, SG & Aiken, LS (2002). Análise de regressão / correlação múltipla aplicada para as ciências do comportamento (3ª ed.). Psychology Press. ISBN 978-0-8058-2223-6.
• "Correlation (in statistics)" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Oestreicher, J. & DR (26 de fevereiro de 2015). Plague of Equals: Um thriller científico de doenças internacionais, política e descoberta de drogas . Califórnia: Omega Cat Press. p. 408. ISBN 978-0963175540.

links externos

• Página do MathWorld no (s) coeficiente (s) de correlação de uma amostra
• Calcule a significância entre duas correlações , para a comparação de dois valores de correlação.
• Uma caixa de ferramentas MATLAB para calcular coeficientes de correlação ponderados
• [1] Prova-que-a-Amostra-Bivariada-Correlação tem-limites-mais-ou-menos-1
• Simulação interativa em Flash sobre a correlação de duas variáveis ​​normalmente distribuídas por Juha Puranen.
• Análise de correlação. Estatística Biomédica
• R-Psicólogo Correlação visualização de correlação entre duas variáveis numéricos