Combinatorialidade - Combinatoriality

Não deve ser confundido com Combinatória .

Na música que usa a técnica de doze tons , combinatorialidade é uma qualidade compartilhada por linhas de tons de doze tons em que cada seção de uma linha e um número proporcional de suas transformações se combinam para formar agregados (todos os doze tons). Assim como os tons de um agregado criado por uma linha de tons não precisam ocorrer simultaneamente, os tons de um agregado criado combinatorialmente não precisam ocorrer simultaneamente. Arnold Schoenberg , criador da técnica de doze tons, muitas vezes combinou P-0 / I-5 para criar "dois agregados, entre os primeiros hexacordes de cada um e o segundo hexacord de cada um, respectivamente."

Combinatorialidade é um efeito colateral de linhas derivadas , onde o segmento ou conjunto inicial pode ser combinado com suas transformações (T, R, I, RI) para criar uma linha inteira. "Derivação se refere a um processo pelo qual, por exemplo, o tricórdio inicial de uma linha pode ser usado para chegar a uma nova linha 'derivada', empregando as operações padrão de doze tons de transposição , inversão , retrógrado e inversão retrógrada . "

As propriedades combinatórias não dependem da ordem das notas dentro de um conjunto, mas apenas do conteúdo do conjunto, e a combinatorialidade pode existir entre três conjuntos tetracordais e quatro tricordais , bem como entre pares de hexacordos e seis díades . Um complemento , neste contexto, é a metade de um conjunto de classes de notas combinatórias e, mais geralmente, é a "outra metade" de qualquer par, incluindo conjuntos de classes de notas, texturas ou intervalo de notas.

Definição

De maneira mais geral, a complementação é a separação de coleções de classes de notas em dois conjuntos complementares, um contendo as classes de notas que não estão no outro. A complementação mais restritiva é "o processo de emparelhar entidades em ambos os lados de um centro de simetria".

Linhas combinatórias de tons de Moses und Aron de Arnold Schoenberg emparelhando hexacordes complementares de P-0 / I-3

O termo "'combinatória' parece ter sido aplicado pela primeira vez à música dodecafônica por Milton Babbitt " em 1950, quando ele publicou uma resenha dos livros de René Leibowitz Schoenberg et son école e Qu'est-ce que la musique de douze filhos? Babbitt também introduziu o termo linha derivada .

Combinação hexacordal

Hexacordes combinatórios de tricórdio do Concerto para Piano de Elliott Carter , mm. 59-60

Uma linha de 12 tons tem combinatorialidade hexacordal com outra linha de 12 tons se seus respectivos primeiros hexacordes (assim como a segunda, porque uma linha de 12 tons forma um agregado por definição) os hexacordes formam um agregado.

Existem quatro tipos principais de combinatorialidade. Um hexacorde pode ser:

e assim:

  • Semi-combinatória (por uma das opções acima)
  • Tudo combinatório (por todos)

A combinatorialidade primária (transposicional) de um hexacórdio refere-se à propriedade de um hexacórdio pela qual ele forma um agregado com uma ou mais de suas transposições. Alternativamente, combinatorialidade transposicional é a falta de classes de pitch compartilhadas entre um hexacórdio e uma ou mais de suas transposições. Por exemplo, 0 2 4 6 8 t, e sua transposição para cima um semitom (+1): 1 3 5 7 9 e, não têm notas em comum.

A combinatorialidade hexacordal retrógrada é considerada trivial, uma vez que qualquer linha tem combinatorialidade hexacordal retrógrada consigo mesma ( todas as linhas de tons têm combinatorialidade retrógrada).

A combinatorialidade inversional é uma relação entre duas linhas, uma linha principal e sua inversão. A primeira metade da linha principal, ou seis notas, são as últimas seis notas da inversão, embora não necessariamente na mesma ordem. Assim, a primeira metade de cada linha é o complemento da outra . A mesma conclusão se aplica à segunda metade de cada linha também. Quando combinadas, essas linhas ainda mantêm uma sensação totalmente cromática e não tendem a reforçar certos tons como centros tonais, como pode acontecer com linhas combinadas livremente. Por exemplo, a linha de Moses und Aron de Schoenberg , acima contém: 0 1 4 5 6 7, isso é invertido para: 0 e 8 7 6 5, some três = 2 3 8 9 t e. 

01  4567     : 1st hexachord P0/2nd hexachord I3
  23    89te : 2nd hexachord P0/1st hexachord I3
complete chromatic scale

A combinatorialidade retrógrada-inversional é a falta de alturas compartilhadas entre os hexacordes de uma linha e sua inversão retrógrada.

Babbitt também descreveu a linha semi-combinatória e a linha totalmente combinatória, sendo a última uma linha combinatória com qualquer uma de suas derivações e suas transposições. Conjuntos semi-combinatórios são conjuntos cujos hexacordes são capazes de formar um agregado com uma de suas transformações básicas (R, I, RI) transposta. Existem treze hexacordes que são semi-combinatórios apenas por inversão. 

(0)  0 1 2 3 4 6 // e t 9 8 7 5
(1)  0 1 2 3 5 7 // e t 9 8 6 4
(2)  0 1 2 3 6 7 // e t 9 8 5 4
(3)  0 1 2 4 5 8 // e t 9 7 6 3
(4)  0 1 2 4 6 8 // e t 9 7 5 3
(5)  0 1 2 5 7 8 // e t 9 6 4 3
(6)  0 1 3 4 6 9 // e t 8 7 5 2
(7)  0 1 3 5 7 9 // e t 8 6 4 2
(8)  0 1 3 5 8 9 // 7 6 4 2 e t
(9)  0 1 3 6 7 9 // e t 8 5 4 2
(10) 0 1 4 5 6 8 // 3 2 e t 9 7
(11) 0 2 3 4 6 8 // 1 e t 9 7 5
(12) 0 2 3 5 7 9 // 1 e t 8 6 4

Qualquer hexacórdio que contenha um zero em seu vetor de intervalo possui combinatorialidade transposicional (em outras palavras: para atingir combinatorialidade, um hexacórdio não pode ser transposto por um intervalo igual a uma nota que ele contém). Por exemplo, há um hexacórdio que é combinatório por transposição (T6): 

(0) 0 1 3 4 5 8 // 6 7 9 t e 2

Nenhum hexacord contém trítonos.

Gruppen ' principal de primeira ordem fileira tom all-combinatória s, embora esta propriedade não é explorado de composição nesse trabalho.
Hexacorde "Ode-a-Napoleão" na forma principal Um dos seis "conjuntos de fontes" do hexacorde totalmente combinatório de Babbitt.

Conjuntos totalmente combinatórios são conjuntos cujos hexacordes são capazes de formar um agregado com qualquer uma de suas transformações básicas transpostas. Existem seis conjuntos de origem, ou conjuntos básicos hexacordalmente combinatórios, cada hexacord dos quais pode ser reordenado dentro de si mesmo: 

(A)  0 1 2 3 4 5 // 6 7 8 9 t e
(B)  0 2 3 4 5 7 // 6 8 9 t e 1
(C)  0 2 4 5 7 9 // 6 8 t e 1 3
(D)  0 1 2 6 7 8 // 3 4 5 9 t e
(E)  0 1 4 5 8 9 // 2 3 6 7 t e
(F)  0 2 4 6 8 t // 1 3 5 7 9 e

Nota: t = 10, e = 11.

Porque os três primeiros conjuntos ( A , B e C ) cada um satisfaz todos os quatro critérios para apenas um valor de transposição, o conjunto D os satisfaz para dois valores de transposição, E para três valores e F , para seis transposições, Babbitt designa esses quatro grupos como hexacordes combinatórios de "primeira ordem", "segunda ordem", "terceira ordem" e "sexta ordem", respectivamente. Observe que o primeiro conjunto, conjunto "A", são as seis primeiras notas de uma escala cromática ascendente, e que o último conjunto, conjunto "F", é uma escala de tom completo.

A combinatorialidade pode ser usada para criar um agregado de todos os doze tons, embora o termo freqüentemente se refira simplesmente a linhas combinatórias declaradas juntas.

A combinatorialidade hexacordal é um conceito da teoria pós-tonal que descreve a combinação de hexacordes, frequentemente usada em referência à música da Segunda escola vienense . Na música que utiliza consistentemente todos os doze tons cromáticos (particularmente doze tons e música serial ), o agregado (coleção de todas as 12 classes de notas ) pode ser dividido em dois hexacordes (coleções de 6 notas). Isso divide o agregado em duas partes menores, facilitando assim a sequência de notas, o progresso entre linhas ou agregados e a combinação de notas e agregados.

As formas principais, P1 e I6, da peça para piano de Schoenberg , op. 33a, a linha de tons apresenta combinatorialidade hexacordal e contém três quintas perfeitas cada, que é a relação entre P1 e I6.

Ocasionalmente, um hexacórdio pode ser combinado com uma versão invertida ou transposta de si mesmo em um caso especial que resultará no agregado (conjunto completo de 12 tons cromáticos).

Uma linha (B ♭ = 0: 0 6 8 5 7 e 4 3 9 t 1 2) usada por Schoenberg pode ser dividida em dois hexacordes: 

B♭ E  F♯ E♭ F  A // D  C♯ G  G♯ B  C

Quando você inverte o primeiro hexacord e o transpõe, o seguinte hexacord, uma reordenação do segundo hexacord, resulta: 

G  C♯ B  D  C  G♯ = D  C♯ G  G♯ B  C

Portanto, quando você sobrepõe o hexacórdio original 1 (P0) sobre a inversão transposta do hexacórdio 1 (I9 neste caso), o resultado é a coleção inteira de 12 tons. Se você continuou o resto da linha invertida e transposta (I9) e do hexachord 2 original sobreposto, você teria novamente o complemento total de 12 tons cromáticos.

Nas Variações de Schoenberg para Orquestra , op. 31, a linha de tons da segunda metade de P1 tem as mesmas notas, em uma ordem diferente, que a primeira metade de I10: "Assim, é possível empregar P1 e I10 simultaneamente e em movimento paralelo sem causar duplicação de notas."

A combinatorialidade hexacordal está intimamente relacionada à teoria dos 44 tropos criados por Josef Matthias Hauer em 1921, embora pareça que Hauer não teve nenhuma influência sobre Babbitt. Além disso, há poucas provas sugerindo que Hauer tinha amplo conhecimento sobre as propriedades inversionais dos tropos antes de 1942, pelo menos. Os primeiros registros sobre relações combinatórias de hexacordes, no entanto, podem ser encontrados entre os escritos teóricos do compositor austríaco e teórico da música Othmar Steinbauer . Ele empreendeu estudos elaborados sobre o sistema tropo no início dos anos 1930, os quais estão documentados em um texto datilografado não publicado Klang- und Meloslehre (1932). Os materiais de Steinbauer datados entre 1932 e 1934 contêm dados abrangentes sobre tricordes combinatórios, tetracordes e hexacordes, incluindo conjuntos semi-combinatórios e todos combinatórios. Eles podem, portanto, ser os primeiros registros da história da música. Uma compilação do material morfológico de Steinbauer tornou-se parcialmente disponível ao público em 1960 com seu script Lehrbuch der Klangreihenkomposition (edição do autor) e foi reimpresso em 2001.

Combinatorialidade tricordal

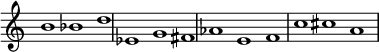
{# (set-global-staff-size 18) \ override Score.TimeSignature # 'stencil = ## f \ override Score.SpacingSpanner.strict-note-spacing = ## t \ set Score.proportionalNotationDuration = # (ly: make -momento 2/1) \ relative c '' {\ time 3/1 \ set Score.tempoHideNote = ## t \ tempo 1 = 60 b1 bes d es, g fis aes efc 'cis a}}
Linha de sons para o Concerto de Webern para Nove Instrumentos Op. 24 .
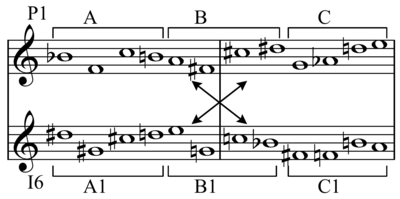
Uma linha derivada totalmente combinatória composta por quatro tricordes : P RI R I.

A combinatorialidade tricordal é a capacidade de uma linha de formar agregados por meio da combinação de tricórdios. "A combinatorialidade tricordal envolve a apresentação simultânea de quatro linhas em pacotes de três unidades." A existência de combinatorialidade tricordal, ou qualquer outra forma, em uma linha não exclui a existência de outras formas de combinatorialidade (pelo menos a combinatorialidade hexacordal trivial existe entre cada forma de linha e seu retrógrado). Todas as linhas derivadas de tricordalmente possuem combinatorialidade tricordal.

Notas

Fontes

  1. ^ a b c Whittall, Arnold . 2008. The Cambridge Introduction to Serialism. Cambridge Introductions to Music , p. 272. Nova York: Cambridge University Press. ISBN  978-0-521-86341-4 (capa dura) ISBN  978-0-521-68200-8 (pbk).
  2. ^ a b Christensen, Thomas (2002). The Cambridge History of Western Music Theory , [não paginado] . Cambridge. ISBN  9781316025482 .
  3. ^ George Perle , Serial Composition and Atonality: An Introduction to the Music of Schoenberg, Berg e Webern , quarta edição, revista (Berkeley, Los Angeles, Londres: University of California Press, 1977), 129-131. ISBN  0-520-03395-7
  4. ^ Peter Westergaard , "Alguns problemas levantados pelos procedimentos rítmicos na composição de Milton Babbitt para doze instrumentos ", Perspectives of New Music 4, no. 1 (outono-inverno 1965): 109-118. Citação em 114.
  5. ^ Kielian-Gilbert, Marianne (1982–83). "Relationships of Symmetrical Pitch-Class Sets and Stravinsky's Metaphor of Polarity", Perspectives of New Music 21: 210. JSTOR  832874 .
  6. ^ Whittall, 103
  7. ^ Whittall, 245n8
  8. ^ Milton Babbitt , revisão sem título, Journal of the American Musicological Society 3, no. 1 (Spring 1950): 57–60. A discussão sobre combinatorialidade está na p. 60
  9. ^ Mead, Andrew (2002). "Composição de Doze Tons e a Música de Elliott Carter", Música de Concerto, Rock e Jazz desde 1945: Ensaios e Estudos Analíticos , pp. 80-81. Elizabeth West Marvin, Richard Hermann; eds. University Rochester. ISBN  9781580460965 .
  10. ^ Harvey, Jonathan (1975). The Music of Stockhausen , pp. 56-58. ISBN  0-520-02311-0 .
  11. ^ David Lewin , "Re: Relações Interválicas entre Duas Coleções de Notas". Journal of Music Theory 3, no. 2 (novembro de 1959): 298–301. p. 300
  12. ^ a b Van antro Toorn, Pieter C. (1996). Music, Politics and the Academy , pp. 128-129. ISBN  0-520-20116-7 .
  13. ^ John Rahn , Teoria Atonal Básica , Longman Music Series (New York e Londres: Longman, 1980): 118.
  14. ^ Castaneda, Ramsey (março de 2016). "All-Combinatorial Hexachords" . Retirado em 1 de junho de 2016 .
  15. ^ Leeuw, Ton de (2005). Música do Século XX: Um Estudo de Seus Elementos e Estrutura . Traduzido por Stephen Taylor. Amsterdam: Amsterdam University Press. pp. 155-157. ISBN 90-5356-765-8.Tradução de Muziek van de twintigste eeuw: een onderzoek naar haar elementen en structuur . Utrecht: Oosthoek, 1964. Terceira impressão, Utrecht: Bohn, Scheltema & Holkema, 1977. ISBN  90-313-0244-9 .
  16. ^ Leeuw 2005 , pp. 154-155.
  17. ^ Diederichs, Joachim. Fheodoroff, Nikolaus. Schwieger, Johannes (eds.). 2007. Josef Matthias Hauer: Schriften, Manifeste, Dokumente 428–440. Viena: Verlag Lafite
  18. ^ Sedivy, Dominik. 2011. Composição de série e tonalidade. Uma introdução à música de Hauer e Steinbauer , p. 70. Viena: edição mono / monocromática. ISBN  978-3-902796-03-5 . Sedivy, Dominik. 2012. Tropentechnik. Ihre Anwendung und ihre Möglichkeiten , 258–264. Salzburger Stier 5. Würzburg: Königshausen & Neumann. ISBN  978-3-8260-4682-7
  19. ^ Neumann, Helmut. 2001. Die Klangreihen-Kompositionslehre nach Othmar Steinbauer (1895–1962) , 184–187, 201–213, 234–236. 2 vols .. Frankfurt et al .: Peter Lang
  20. ^ Morris, Robert (1991). Class Notes for Atonal Music Theory , p. 82. Frog Peak Music. ASIN  B0006DHW9I [ISBN não especificado].